对于TE 波，利用理想边界条件代入 ，则有

利用不变性变换矩阵得到其横向场为

利用边界条件 ，有

设 是第一类 阶Bessel 函数的导数的第 个根，由于 Bessel 函数是没有「第零个根」的，所以 。则 。由关系 有

以及

对于 TM 波，设 是第一类 阶Bessel 函数的第 个根。由 ，有

• 对于 TE11，有
• 对于 TE21，有
• 对于 TE01，有
• 对于 TM01，有
• 对于 TM11，有
• 对于 TM21，有

TE11 截止波长最长，是圆波导的主模。写出其场表达式

因此 TE11 模横纵截面场分布为分别为

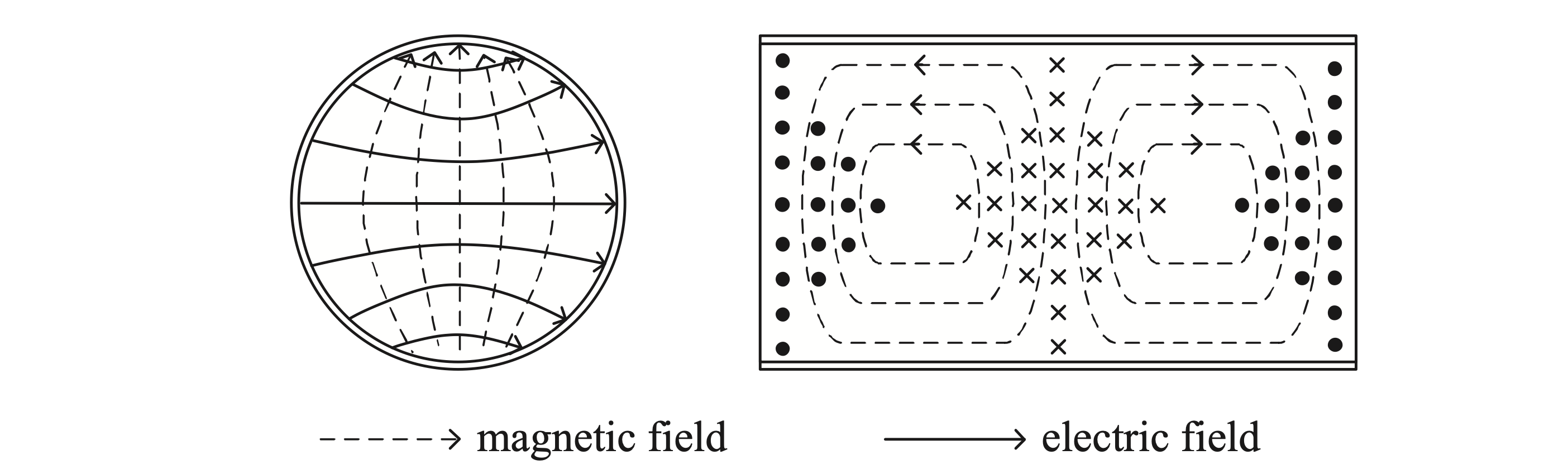
立体图为

• ，取 ， 或 时 ，而 或 时， 最大
• ，考察 。 时， 最大； 时正好消掉， 项为零，因此

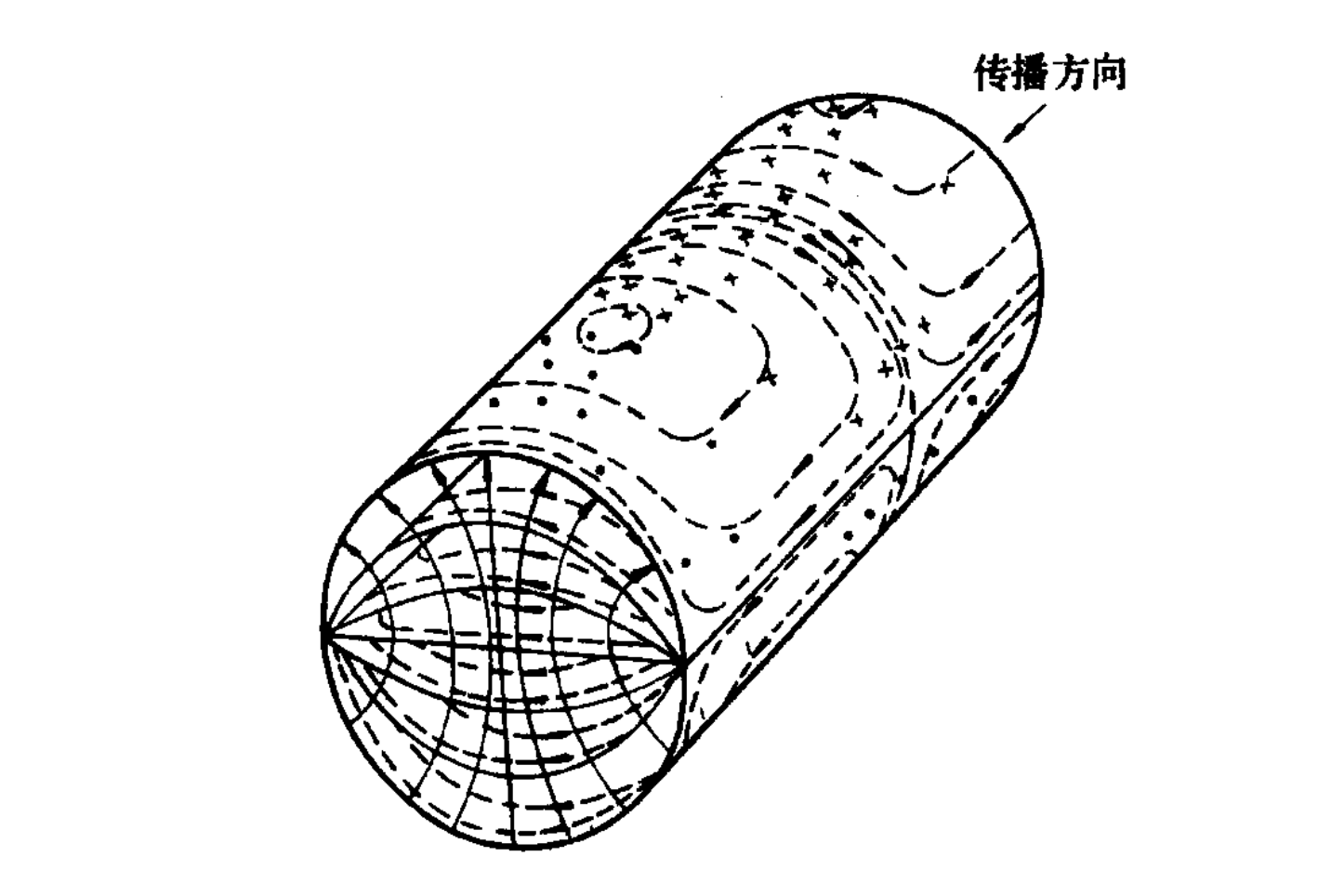
TE 11 波型的场结构与矩形波导 TE10 模的场结构很类似，因此很容易被矩形波导中的 TE10 波型所激励，利用此性质，可以进行“方圆转换”。

TE11 波型的缺点是，当波导加工不完善或波导内有微小的不均匀性存在时，都会使场结构的极化面产生旋转

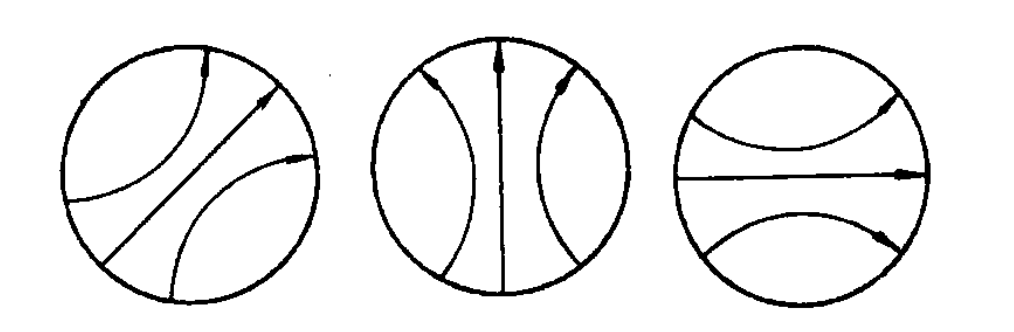
因此在有的场合不采用这种波型。

对于 TE01 模，其解为

同样可以画出场的分布图为

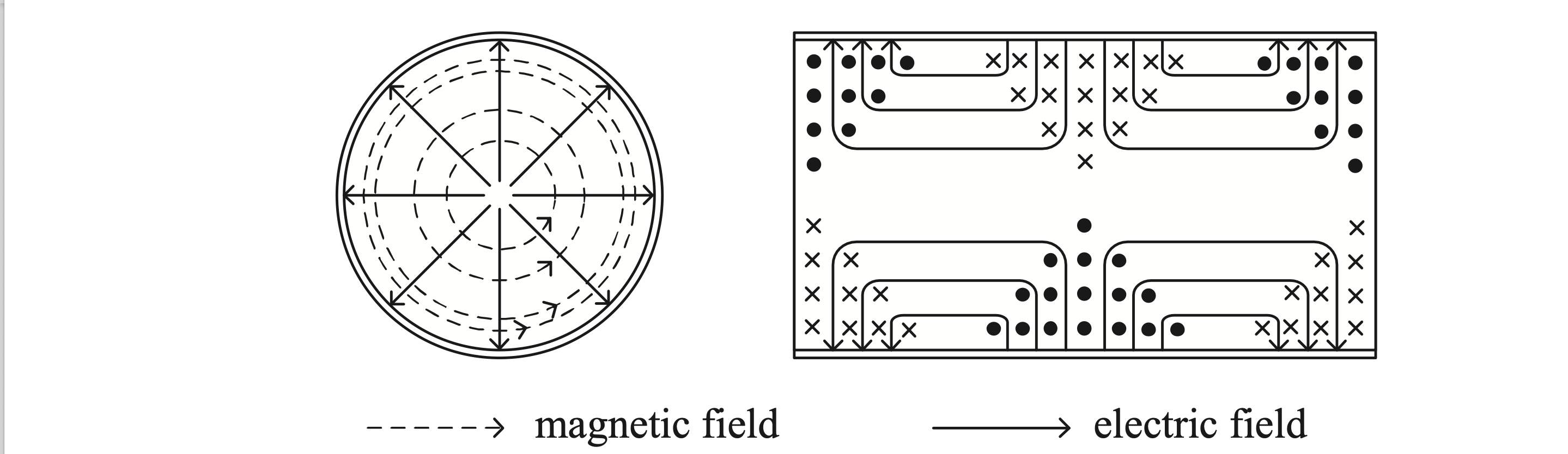
由于表面电流公式 ，因此 TE01 模的电流表示为

对于 TE01 模，其场结构具有如下特点

1. 电磁场沿 方向不变化，即具有轴对称性
2. 电场只有 分量，在中心和管壁附近为零
3. 在管壁附近只有 分量磁场，故管壁只有 分量，没有纵向电流，因此导体损耗较小。

因此，当传输功率一定时，随着频率增高，损耗将减小，衰减常数变小。这一特性使得 TE01 适用于毫米波长距离高低损耗传输与高 Q 值圆柱谐振腔的工作模式。

实际上，不仅是 TE01，而是所有的 TE0n 波型的导体衰减系数 都会随着频率的升高而降低。如图所示

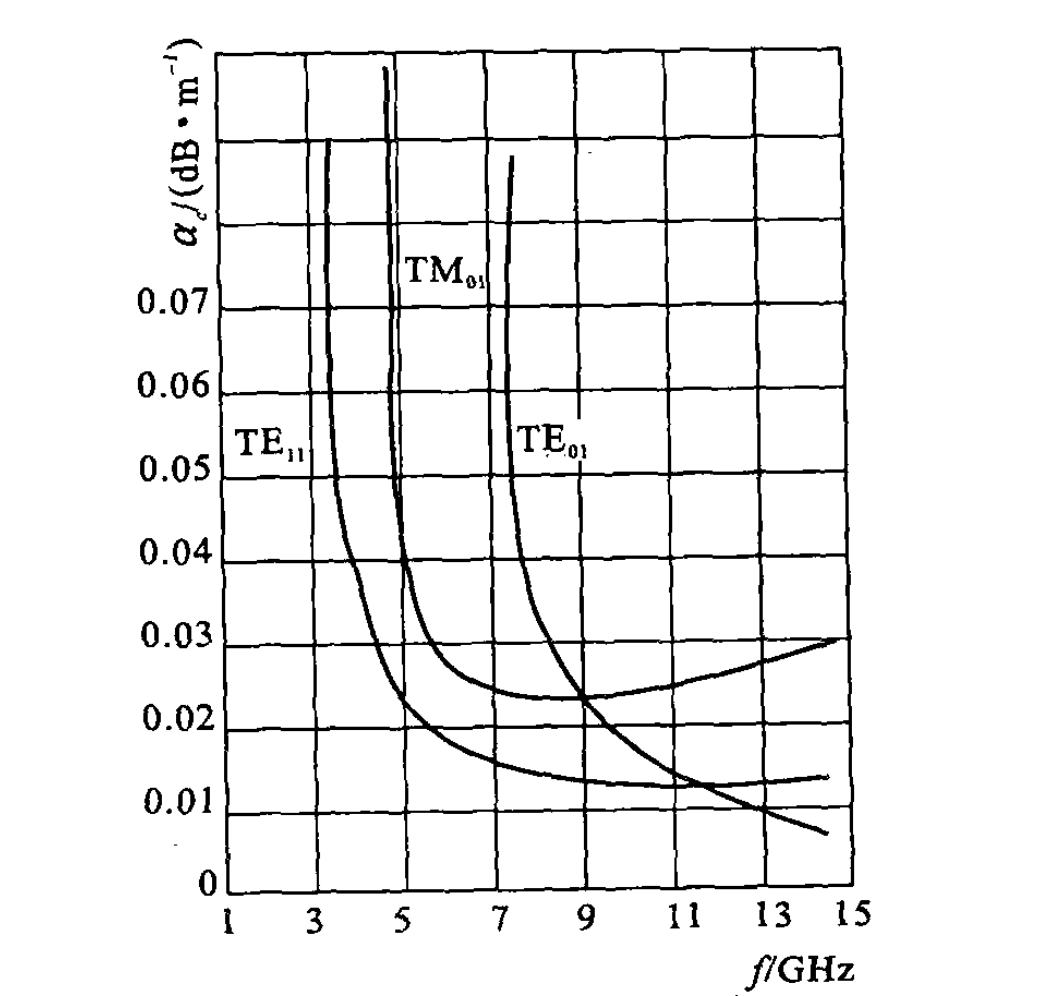
从 TE0n 场分量表达式可以看出

在传输功率不变的情况下，随着频率升高，场的横向分量 相对于纵向分量 增大了，即 相对地减小了，因此衰减系数 变小了。

与 TE01 模是类似的

由于 TM01 模具有 方向上的旋转轴对称性，可以用作旋转关节。