支持向量机

支持向量机(Support Vector Machine, SVM)是由Cortes和 Vapnik 于1995年首先提出。SVM 在解决小样本、非线性等分类问题中表现出许多特有的优势，并能够推广到函数拟合等有关数据预测的应用中。

传统的统计模式识别方法只有在样本趋向无穷大时，其性能才有理论的保证。统计学习理论（STL）研究有限样本情况下的机器学习问题。SVM的理论基础就是统计学习理论。传统的统计模式识别方法在进行机器学习时，强调经验风险最小化。而单纯的经验风险最小化会产生“过学习问题”，其推广能力较差。

支持向量机以训练误差作为优化问题的约束条件，以置信范围值最小化作为优化目标，即 SVM 是一种基于结构风险最小化准则的学习方法，其推广能力明显优于一些传统的学习方法。

问题引入

logistic 回归将特征的线性组合作为自变量，通过Sigmoid 函数，将自变量映射到区间上，作为分类为正例的概率值

其中为预测标签值。注意到的值或分类结果只和有关，由此得到决策边界的概念，即

从决策边界的角度来说，我们希望分类器达到的效果

$标签时，$ $标签时，$

几何直观上，样本点距离决策边界的间隔越大越好。本章从间隔的角度去重新考虑分类问题。

基本概念

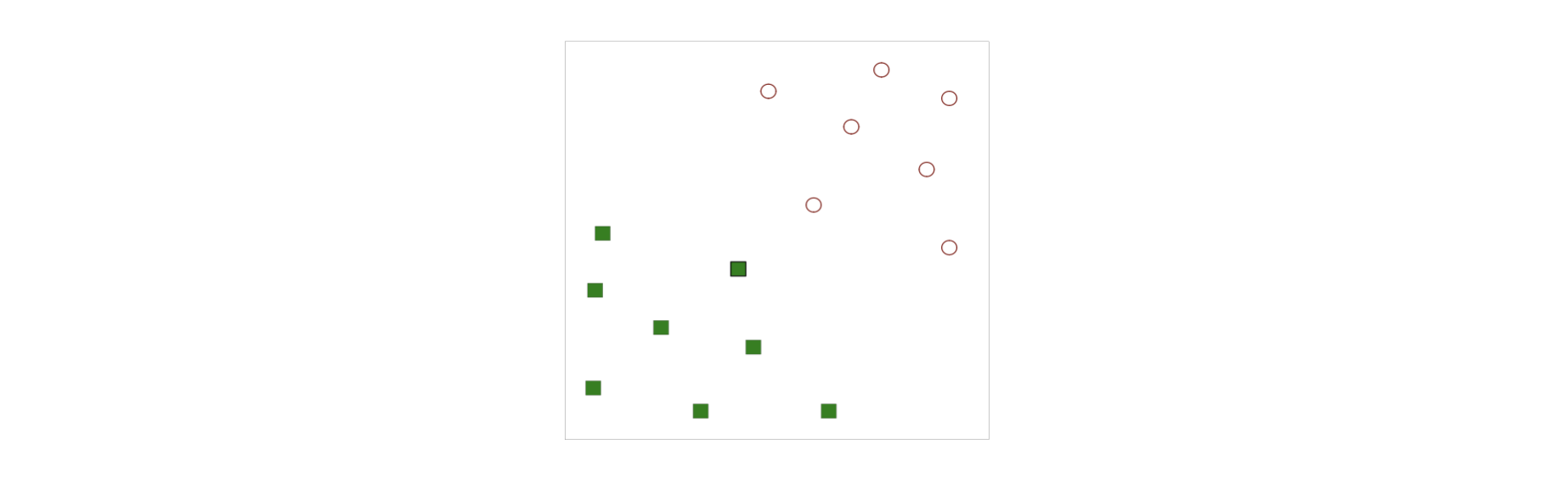
SVM是在两类线性可分情况下，从获得最优分类面问题中提出的。一个两分类问题，其中“红色空心圆圈”表示一类，“绿色实心正方形”表示另一类。问题：如何在二维平面上寻找一条直线，将这两类分开。

img-2024-04-11 18-49-21.png

从几何的观点来看，决策边界是一个划分超平面。在样本空间中，划分超平面定义为

为法向量，决定超平面的方向
为位移项，决定超平面与原点之间的距离

直觉上认为，期望找到一个所谓的最优分类面，要求分类面不但能将两类正确分开，而且应使分类间隔最大。根据几何知识，任意样本点到超平面的距离为

在 SVM 中，定义

其中表示正例。表示反例。选择 $，$ ，而不是以零为划分标准，表示有更高的分类概率。这里的的选择单纯是因为其作为常数比较简单，此常数是任取的。SVM 的解决方案具有缩放不变性，这意味着如果你将和同时乘以一个正常数，这不会影响分类决策的结果。也就是说，如果有一个解和，你可以通过调整和的大小，使得最近的数据点恰好满足或

使上述等号成立的样本点被称为「支持向量」（Support Vector）

对于支持向量有，因此两个异类支持向量到超平面的距离为

称之此距离为「间隔」（Margin）。直觉上来说，Margin 越大，对新样本的分类（抗干扰）能力越强。

优化方法

最优化问题

我们希望分类器具有如下效果

$标签时，$ $标签时，$ 从间隔的角度考虑，希望获得具有最大的划分超平面。即寻找满足约束的，使得间隔最大。

因此优化目标可以等价表示为一个条件极值问题

我们希望通过求解上述优化问题，来得到大间隔划分超平面所对应的模型

这是一个凸二次规划问题，能用现成的优化计算包计算

例题

已知一个数据集的样本为

其中正样本为，负样本为，求最大间隔划分超平面，其中 )

解：根据 SVM 的基本型，构造约束最优化问题

且有

求得此最优化问题的解，所以最大间隔分离超平面为

其中与为支持向量。

拉格朗日对偶问题

使用Lagrange 乘数法，对每条约束添加 Lagrange 乘子，可得到其对偶问题。SVM 基本型的 Lagrange 方程可以写为

其中。然后根据 Lagrange 乘数法的要求，令对和的偏导数为 0，可得

代入拉格朗日方程得到

进一步化简

根据拉格朗日对偶性原理，此时我们需要最大化，从而得到了 SVM 的对偶优化问题：

此时的对偶问题仅涉及拉格朗日乘子和训练数据，而原始问题不仅设计拉格朗日乘子，还涉及决策边界的参数。尽管如此，这两个优化问题是等价的。解出后，划分超平面方程可写成

因此，通过对偶问题解出拉格朗日乘子向量，即可求得超平面。由于中有不等式约束，上式过程需要满足 KKT 条件，即

以上约束条件说明，对于任意训练样本总有或。

若，则说明该样本不会再划分超平面的求和式中出现，即不会对产生影响
若，则，对应的样本点为支持向量。

所以，支持向量的模型训练完成后，大部分训练样本都不需要保存，最终模型只与支持向量有关。

拉格朗日对偶问题式接出后，按照求解，即

其中可以通过求解支持向量公式得到，即

上式中为支持向量，为其对应的最优拉格朗日乘子。

由于可能存在多个支持向量，且是通过数值计算得到的，因此可能存在数值误差，计算出的值可能不唯一，取决于使用的支持向量。实践中，通常使用求得的平均值作为决策边界的参数。

最后求得的划分超平面方程可写为

此外还有一种改进算法，称为SMO 算法。

例题

给出下图所给的二维数据集，它包含 8 个训练实例。使用二次规划的方法，可以求解公式给出的优化问题，得到每一个训练实例的拉格朗日乘子，如下表的最后一列所示

			拉格朗日乘子
0.3856	0.4587	1	65.5261
0.4871	0.6110	-1	65.5261
0.9218	0.4103	-1	0
0.7382	0.8936	-1	0
0.1763	0.0579	1	0
0.4057	0.3529	1	0
0.9355	0.8132	-1	0
0.2146	0.0099	1	0

不难发现，只有前两个实例具有非零的拉格朗日乘子，这两个实例对于数据集的支撑向量。

令为决策边界参数，则有

位移项可以用每个支持向量进行计算

对这些值取平均，得到，所以对应的划分超平面为

例题

（课堂作业出现过）

已知一个数据集的样本为。其中正样本为，负样本为，求最大间隔划分超平面，其中 )

解：根据 SVM 的对偶优化问题

注意到约束条件，则，代入上式消去

接下来尝试对其进行最大化。首先对分别求偏导数，可知在点取得极值，但该点不满足约束条件，所以最大值应该在边界上达到

当时，最大值
当时，最大值

于是在达到最大，此时。这样，对应的实例点是支持向量。接下来求解超平面参数和

因此，超平面为

例题

对于样本空间中的一划分超平面，有，则判断如下向量是否为支持向量，并求出间隔

解：

直接代入超平面

，故不是支持向量
，故不是支持向量
，故不是支持向量
根据间隔的定义

线性不可分

（理解概念即可）

在前面的讨论中，我们总是假设样本点是线性可分的。但实际问题中，这一假设并不总是成立。

现实任务中往往很难确定合适的核函数是的训练样本在特征空间中线性可分
即使找到了某个核函数使得训练数据在特征空间线性可分，也很难断定这个貌似线性可分的结果不是因为过拟合造成的

利用「核函数」（Kernel Function）可以将原始样本点映射到一个高维空间，从而使其线性可分。

由此，引入「软间隔支持向量机」，允许 SVM 在一些样本上出错，即允许某些样本不满足约束

支持向量回归

七、小结

SVM 的目标是对特征空间划分的最优超平面，核心思想是最大化分类间隔。SVM 利用内积核函数项高维空间进行特征映射，使得原线性不可分特征变得可能。
支持向量是 SVM 的训练结果，在 SVM 分类决策中起决定作用的是支持向量。
SVM 得到的决策函数只由少量的支持向量所决定，计算法杂性取决于支持向量的树木，而不是样本空间的维数，能够避免了「维数灾难」
SVM 方法已经在图像识别、信号处理和基因图谱识别等方面得到了成功的应用
支持向量方法也为样本分析、因子筛选、信息压缩、知识挖掘和数据修复等提供了新工具
SVM 本质上是二分类器，可通过前面讲的多分类学习方法扩展到多分类问题。

SVM 的优点

有严格的数学推理；
小样本分类器；
特别适合处理复杂的非线性分类问题。

缺点

训练时间非常长；
无法直接处理多分类问题。