核函数

在支持向量机中尝试对非线性可分样本，可以利用「核函数」（Kernel Function）可以将原始样本点映射到一个高维空间，从而使其线性可分。

数学证明，如果原始空间是有限维，则一定存在一个高维特征空间使样本线性可分。 或从哲学的角度来说，世界上本来没有两个完全一样的物体，对于所有的两个物体，可通过增加维度来让他们最终有所区别。

img-2024-04-11 18-56-30.png

令表示样本映射后的特征向量，则「核函数」满足下式

即根据泛函理论，与在特征空间的内积等于他们在原始样本空间中通过函数计算的结果。映射后的特征空间维度可能很高，直接计算通常都是困难的，这就是为什么我们需要采用核函数。在核函数的作用下，SVM 相当于如下形式的网络结构

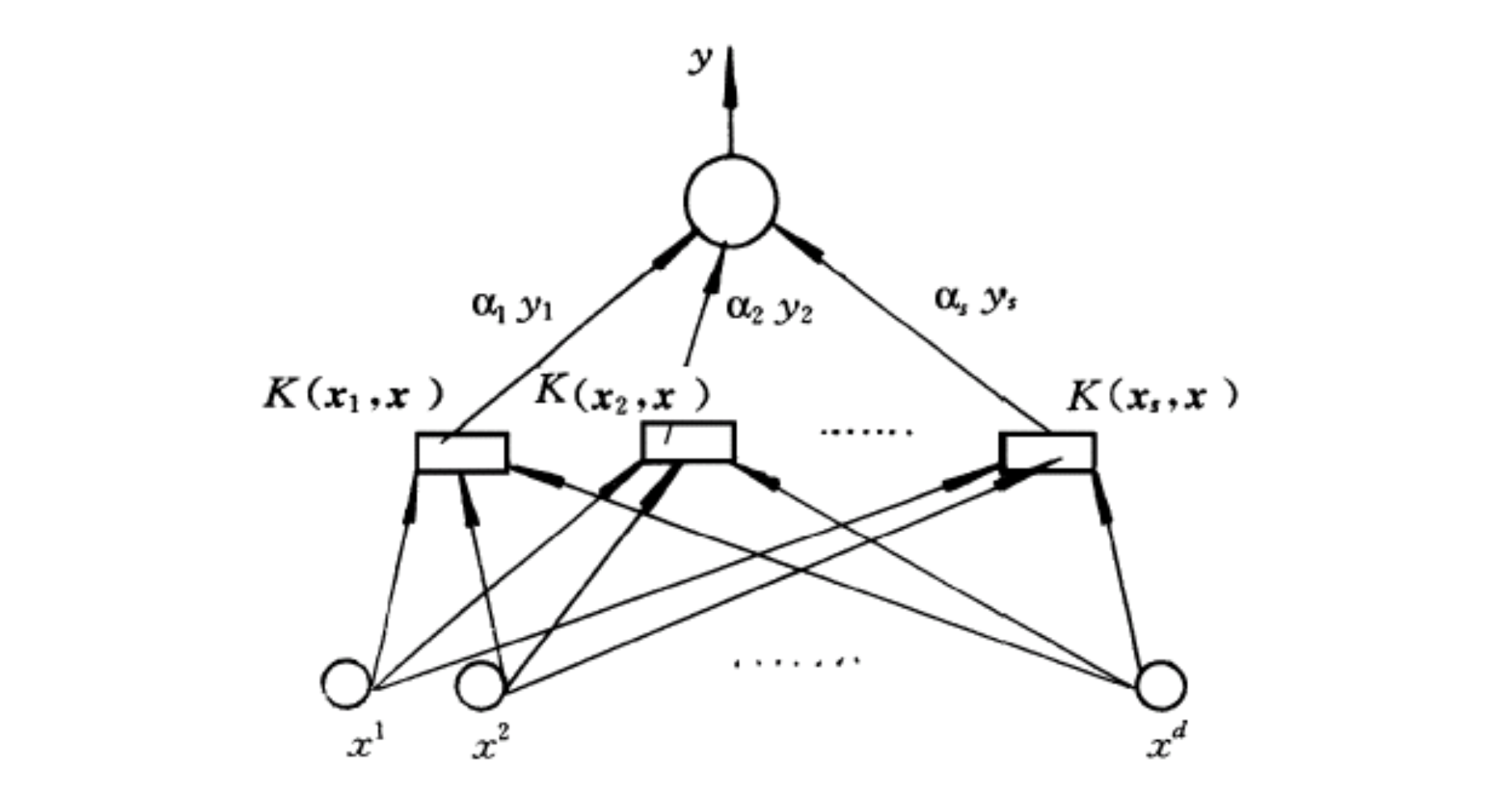
img-2024-04-11 18-57-54.png

支持向量机的对偶优化目标可以用核函数表示为

解出后及相应的支持向量后，得到划分超平面的核函数展开式，亦称为「支持向量展开式」

定理

（不重要）

令为输入空间，是定义在上的对陈函数，则是核函数，当且仅当对于任意数据，「核矩阵」（Kernel Matrix）总是半正定的

上述定理表明，只要一个对称函数所对应的核矩阵为半正定矩阵，就能作为核函数使用。事实上，对于一个半正定核矩阵，总能找到一个与之对应的映射

常用的核函数

在不知道特征映射的形式时，我们并不知道什么样的核函数是合适的，而核函数也是隐式地定义了这个特征空间。“核函数选择”称为支持向量机的最大变数。几种常用的核函数有

线性核

多项式核

其中，为多项式的次数。

高斯核

其中，为高斯核的带宽

拉普拉斯核

其中，为拉普拉斯核的带宽

Sigmoid 核

其中为双曲正切函数，

选用核函数的一些经验：文本数据常用线性核，未知分布数据可选用高斯核。

组合性

核函数也可以用函数组合得到，设均为核函数，则下面的组合也是核函数

线性性

对于任意的正数和，有核函数

直积

乘积

对于任意函数有

求解 XOR 问题

给出四个样本和期望的响应如下所示

输入	期望响应
	-1
	+1
	+1
	-1

可见此数据集线性不可分，为 XOR 问题。这种情况往往需要往高维特征空间进行映射，使其线性可分。将一个样本表示为，取以下核函数进行映射

展开为

根据核函数展开式，可以得到基函数，也就是输入向量在高维空间的映射

在此例中，输入为二维空间向量，通过基函数被映射到了六维空间。下图左图为六维空间在平面的投影，可以看出数据变得线性可分。下图中右边为六维空间的支撑向量所在决策平面对应于原平面为双曲线

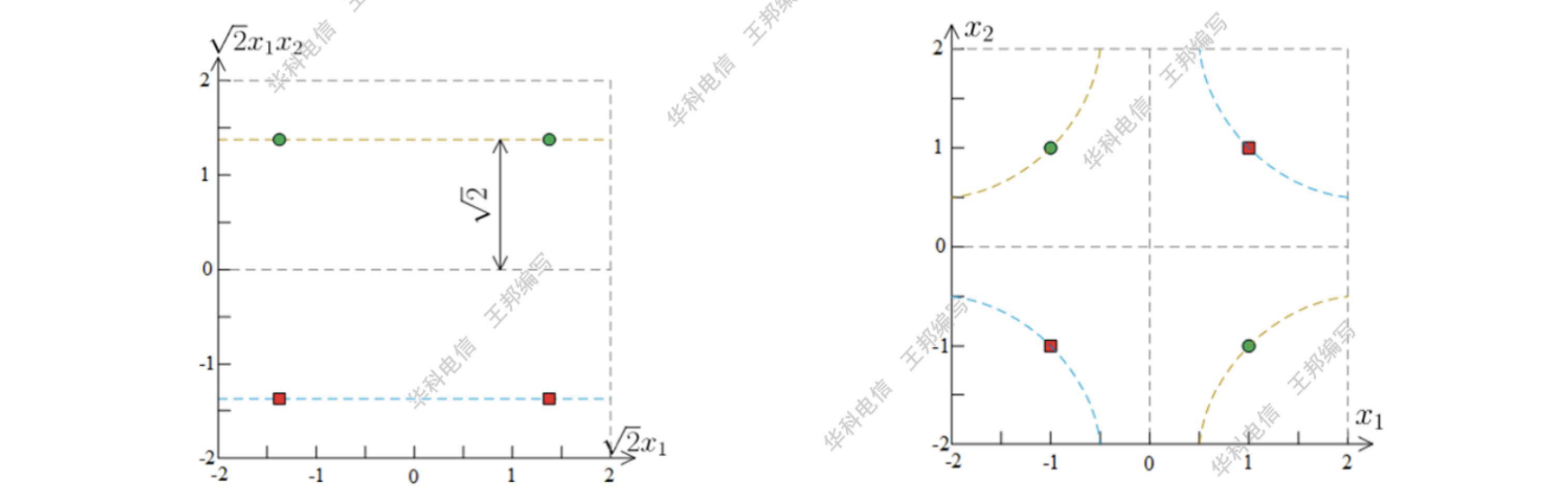
img-2024-04-11 18-09-19.png

将输入样本代入式中，可得到的矩阵中各元素的值为

接下来需要寻找拉格朗日乘子使得以下目标函数最大

将数据带入，即使下式最大化

约束条件为

对求偏导并令导数等于 0 可得

解得拉格朗日系数的最优值为

观察可知，没有拉格朗日系数等于零，所以四个样本都是支持向量。此时对应的目标函数最优值为。接下来求解对应六维空间的划分超平面对应的法向量

由 KKT 条件可对每个支持向量

对这些值取平均得到。根据划分超平面的定义可得，XOR 问题对应的模型为

对应的划分超平面为为

例题

现有一个一维数据，有

解：

选择如下的二次项核函数，设置，从下式中求解

根据支持向量展开式，得到

满足，得到，故最后得到

例题

假设输入空间是，核函数是，试找出其相关的特征空间和映射

解：

将核函数展开

容易得到一种映射为

此时的特征空间为三维。另一种映射为

此时的特征空间为四维