软间隔支持向量机

在普通的支持向量机的讨论中，样本点或样本点映射后都是完全线性可分的。但是现实中存在问题

1. 现实任务中往往很难确定合适的核函数是的训练样本在特征空间中线性可分
2. 即使找到了某个核函数使得训练数据在特征空间线性可分，也很难断定这个貌似线性可分的结果不是因为过拟合造成的

由此，引入「软间隔支持向量机」

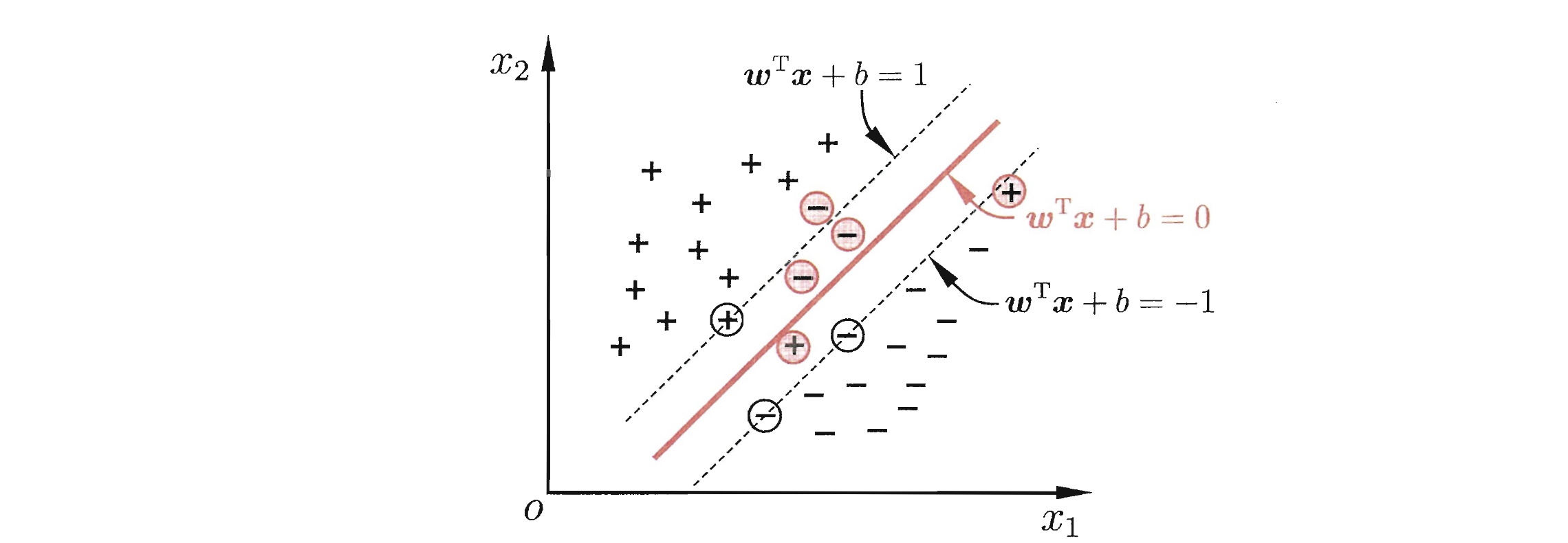
软间隔支持向量机允许 SVM 在一些样本上出错，即允许某些样本不满足约束

对于软间隔，在最大化间隔的同时，还希望不满足约束的样本尽可能少，所以优化目标式改写为

其中 是常数，称为「惩罚因子」， 称为「0/1 损失函数」，其定义为

惩罚因子 决定了对离群点带来损失的重视程度。当所有离群点的松弛变量的和一定时， 越大，对目标函数的损失也越大，此时就暗示着非常不愿意放弃这些离群点，最极端的情况是把 定为无限大，这样只要稍有一个点离群，目标函数的值就变成无限大，马上让问题变成无解，这就退化成了硬间隔问题。

惩罚因子 不是一个变量，整个优化问题在解的时候， 是一个必须事先指定的值，指定这个值以后，解一下，就得到一个分类器，然后用测试数据看看结果好不好，不好再换一个 的值。如此就是一个参数寻优的过程。

由于 非凸，非连续，数学性质不好，常用以下损失函数替代

• hinge 损失
• 指数损失
• 对数损失

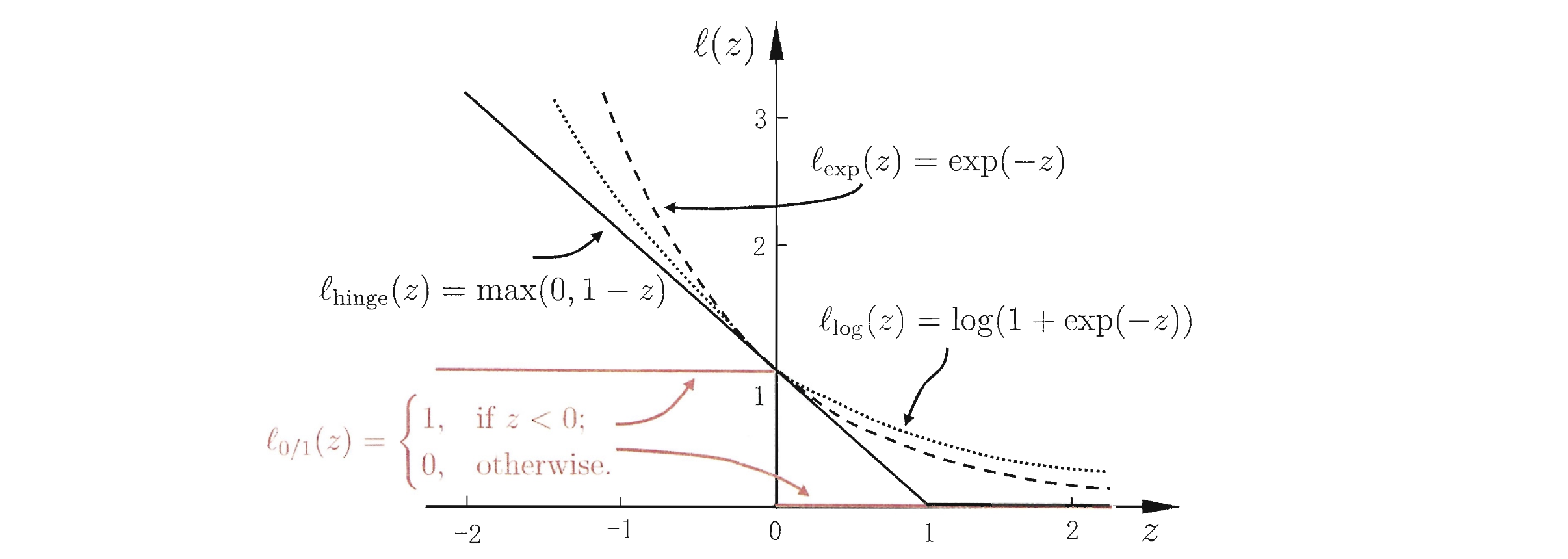
若用 hinge 损失代替 ，则优化目标式为

其中 称为「松弛变量」（Slack Variable），且

变量 记录了对 分类的错误代价。- 以某些点不能正确划分为代价，来换取更大的分隔间隔。这就是所谓的「软间隔支持向量机」，解出 即可得到划分超平面。

对于软硬间隔的对偶问题式对比可以发现，两者唯一不同是对偶变量的约束条件

• 软间隔要求
• 硬间隔要求

类似的，KKT 条件也会做出相应的变化。但是，软间隔支持向量机和硬间隔下一样，最终模型仅与支持向量有关。

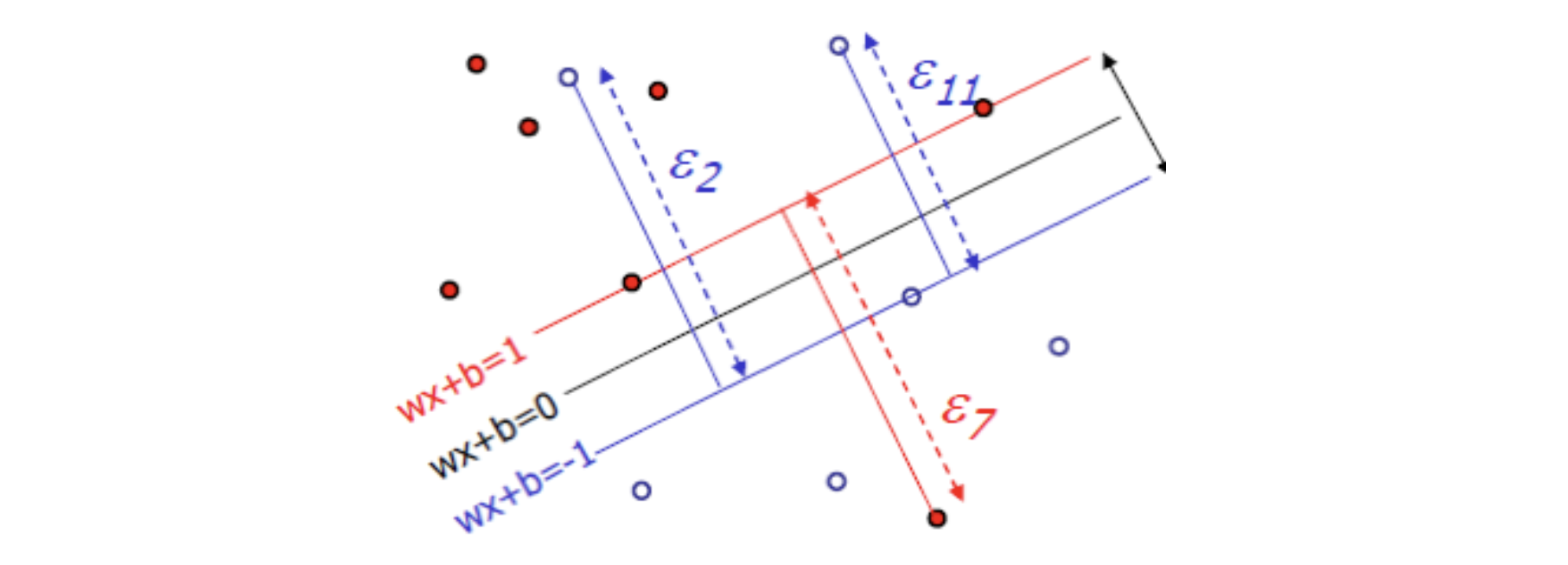
• 因为松弛变量是非负的，因此样本的函数间隔可以比1小。
• 函数间隔比1小的样本被叫做离群点，放弃了对离群点的精确分类，这对分类器来说是种损失。
• 并非所有的样本点都有一个松弛变量与其对应。只有“离群点”才有。
• 松弛变量的值实际上标示出了对应的点到底离群有多远，值越大，点就越远。
• 放弃这些点也带来了好处，那就是超平面不必向这些点的方向移动，因而可以得到更大的几何间隔（在低维空间看来，分类边界也更平滑）。