双支节匹配
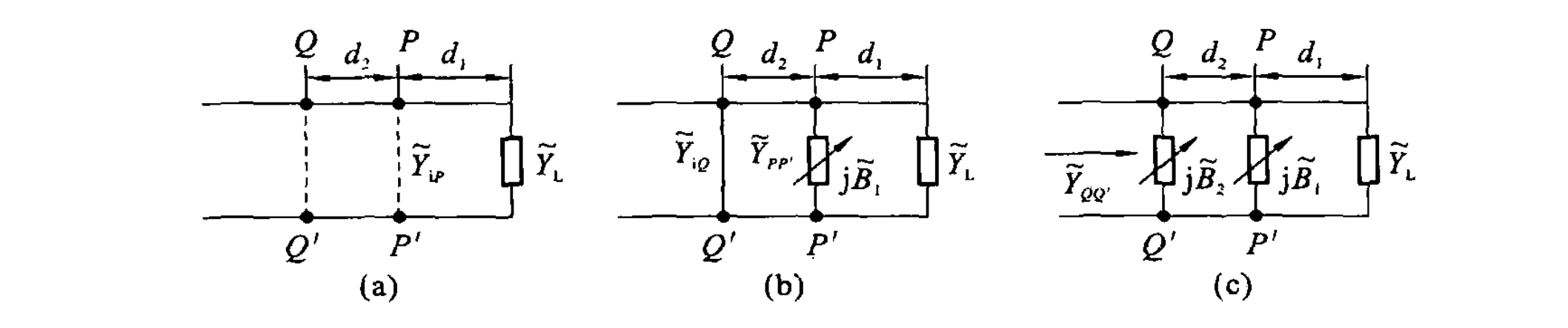
第一个支线插入位置距离负载
在双枝节匹配中,匹配枝节的接入位置
求解
为了让传输线匹配,从
其中
其中,让
但是如何保证匹配前的主线导纳实部恰好为 1 呢?这就是
解析法
记负载和
记不考虑
其中归一化输入导纳
由于
因此解析法的求解过程表示为,先求出
经过
根据
需要注意的是,在
圆图法
设想一下,假如
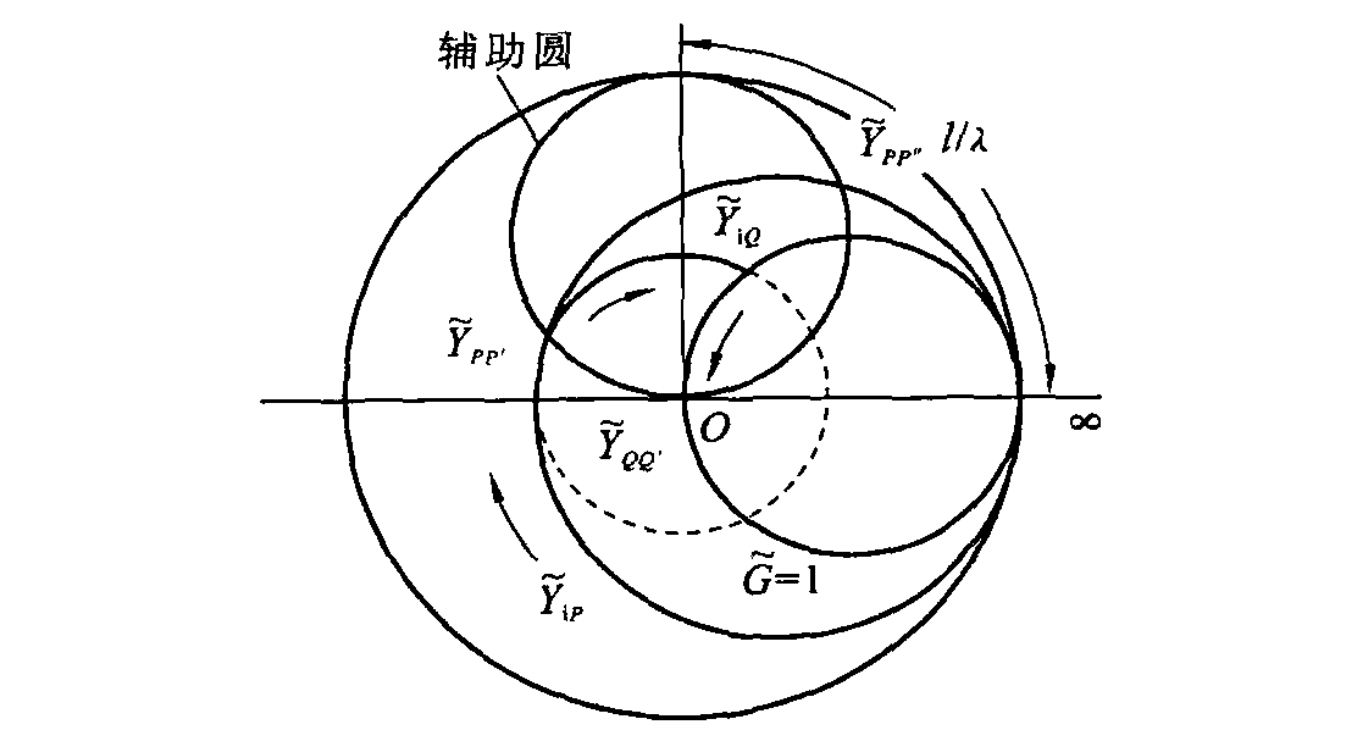
因此现在匹配条件变成,只要让
在大多数情况下,这两个圆有两个交点
以
以上的过程可以总结为,首先对距离负载
需要注意的是,在使用
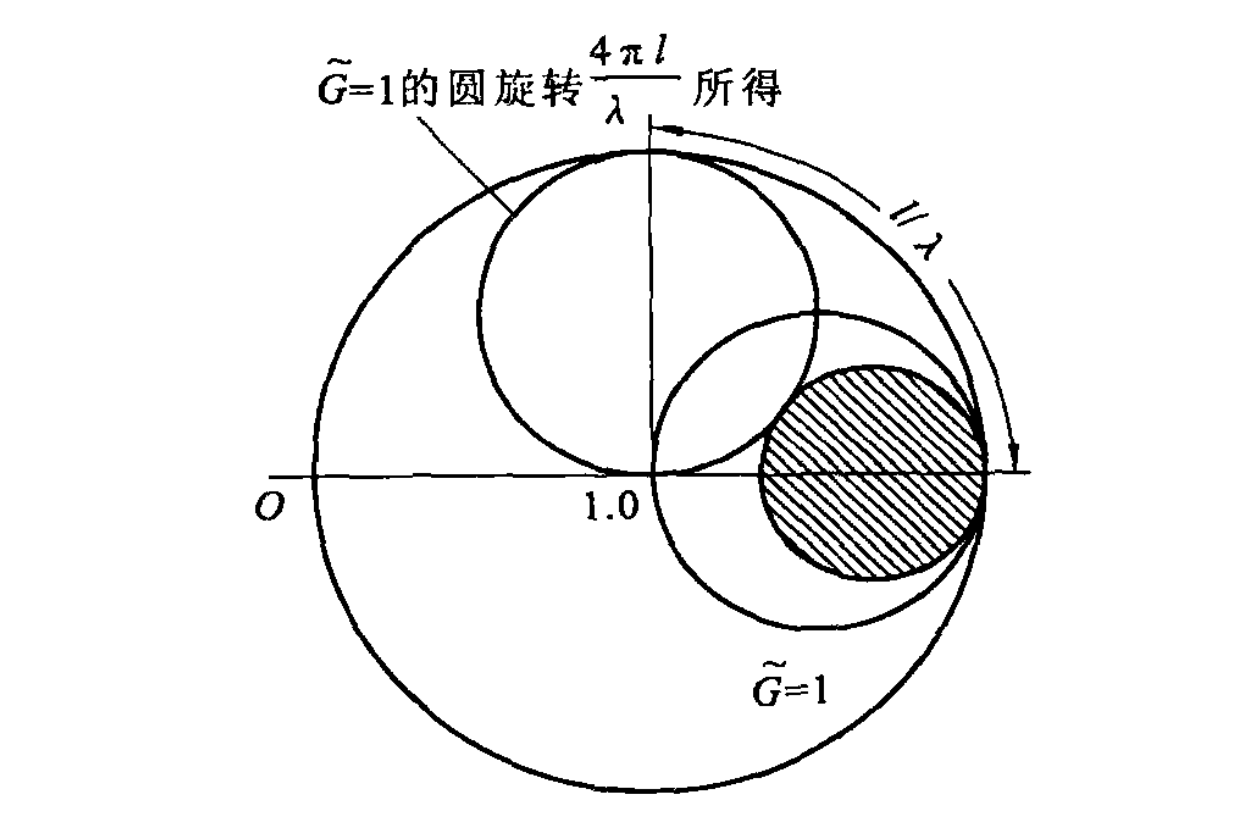
那么无论如何调整
对于辅助圆和电阻圆要相交,则要求构成的的直角三角形满足
解得
例题
归一化负载导纳为
解析法:
本题直接将
解出
其中
代入
因此再根据
然后推导死区问题。对于
此式不一定总是有解的。具体来说
要求
方法二,史密斯圆图法。
首先根据负载画出
对应到短路枝节,向源端,即顺时针旋转电长度,从 0.25 旋转到 0.444,旋转了
然后再将两个
对应枝节电纳分别
例 2
利用双株短路支线对传输线(主线)进行匹配,设第一支线(靠近负载)距终端负载为
解析法:归一化负载阻抗
归一化输入阻抗为
代入
解出
因此
然后再讨论
分别代入
图解法:首先求出
得到
在 Smith 圆图上分别找出这两个等电纳圆与
然后将两个
在 Smith 圆图上分别找出这两个等电纳圆与
例 3
利用双株短路支线对传输线(主线)进行匹配,设第一支线(靠近负载)距终端负载为
解析法:归一化负载阻抗
归一化输入阻抗为
代入
解出
因此
然后再讨论
分别代入
图解法:由于这题 P 支路并联,但 Q 支路串联,如果用逆向思维,在使用 Q 支路进行串联匹配的时候,对应在 Smith 圆图上使用的肯定是阻抗点而非一般习惯上的导纳点。
由于
首先求出
相减得到
在 Smith 圆图上分别找出这两个等电纳圆与
然后将两个导纳点
得到
在 Smith 圆图上分别找出这两个等电抗圆与