单支节匹配

「单支节匹配」是一种枝节匹配器，与其原理为在传输线距离负载 处并联一个长度为 的短路支线。结构如下

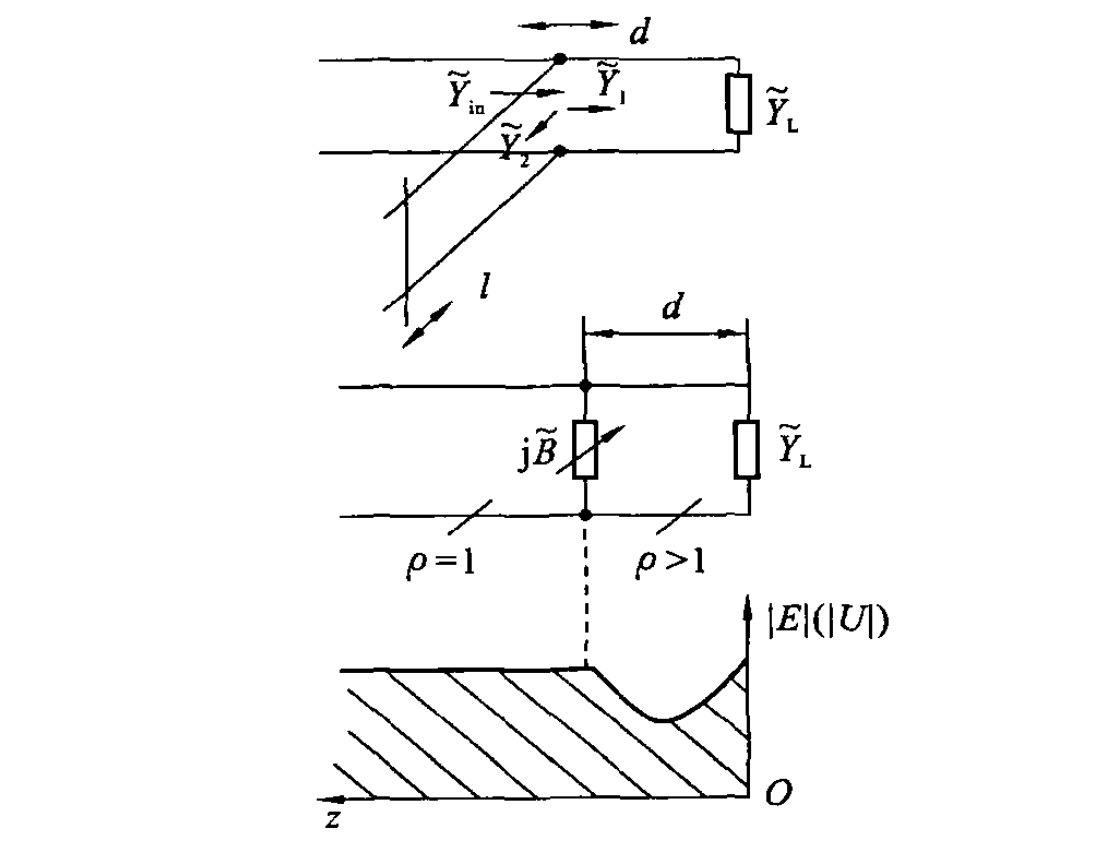
img-2024-05-06 18-41-57.png

这类问题需要求解出 和 的取值。

计算

解析法

记匹配前的输入导纳为 ，匹配后则为

为了使传输线匹配，必须使在直线并联出，向负载看去总的归一化输入导纳为 1，即

由于短路支路只能提供电抗，即

得到归一化输入导纳为

首先，根据输入导纳公式，归一化后有

此时是在匹配支路介入前的，要求在匹配点 应该至少满足 ，因此要求
化简完为

当 时为关于 的一元一次方程，解得

而 时为关于 的一元二次方程

解得

此时会解出两个 解。为了让 有意义，一般取 内的值，两个 将会对应两个值。

确定接入位置 后，接下来确定长度 。在微波传输线纯驻波状态中已知对于长度为 的短路线，阻抗变换公式为

其中 这里就是分支点看短路支路的输入阻抗，此时应与负载支路的电抗相抵消，因此有

解得

其中 为特性导纳， 为

图解法

用 Smith 圆图，依据归一化负载导纳 ，在圆图上坐落于 ，然后在等反射系数圆上旋转得到需要的 。因为已经确定到电阻部分为 1，因此交点为电导为 1 的等电导圆 。如下图，有 两个交点。

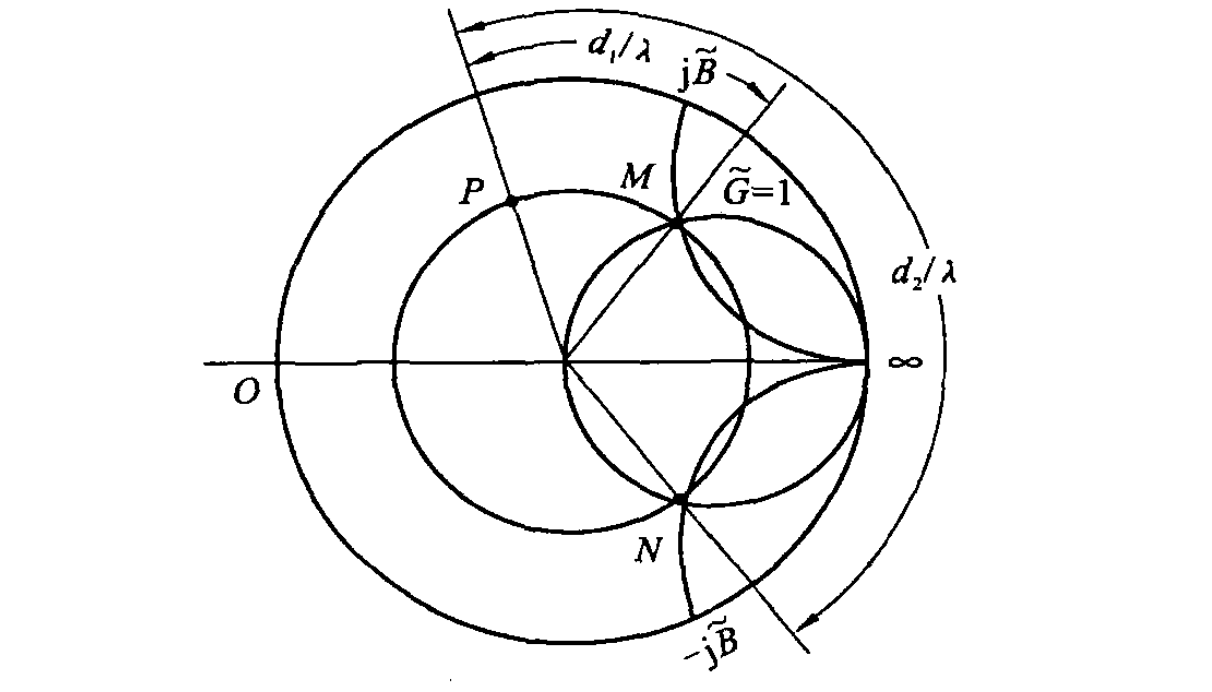
img-2024-05-06 18-49-14.png

根据转过的角度或者电长度可以得到距离 。 两个交点说明有两组解

确定好 两个点后，在圆图上读出对应的电纳，例如 处归一化电纳为 的话，表示接入处需要产生 的电纳才能抵消影响。

接下来需要分别求解 。大多数情况下，主线和支节线的特性阻抗一样，因此不用重新归一化，但如果二者不同，在接下来的求解之前，可能需要根据支节线的特性阻抗重新进行归一化

注意，现在画图的语境是导纳的，因此短路点不是最左侧的 ，而是旋转 180 度的 。

由于接入的是并联短路支节，因此此时从短路点开始。由于是在导纳的语境下，因此短路点为 而不是 。现在沿着 的圆向源端（顺时针）旋转，直到旋转到 的点。所转过的角度即为 。

例题

已知 ，传输线长度为 ，现要求进行单枝节匹配。

解：方法一，解析法，首先求负载的归一化输入导纳

由于要求归一化实部为 ，即

解得 或 ，解得 ，继而得到

方法二，圆图解法。归一化得到

从圆图上读出

例题

传输线的终端负载为 ，用并联单株短路线进行匹配，主线和支线的特性阻抗均为，试分别用解析法和圆图法，求支线的位置和长度。

解析法：

归一化输入导纳为

然后取实部得到

代入 得到

解得 。然后考察所需支节长度。

其中 为 ， 为从接入点看负载支路的电抗，其值为

代入数据得到 ，因此

图解法：

归一化负载阻抗为 ，在图上 ，点，然后沿着等反射系数圆转过 180 度找到归一化负载导纳为 在 Smith 圆图上画出 位于 其标度为 ，沿着等反射系数圆，旋转到等电阻圆 上，找出两个交点 ，其标度分别为 和

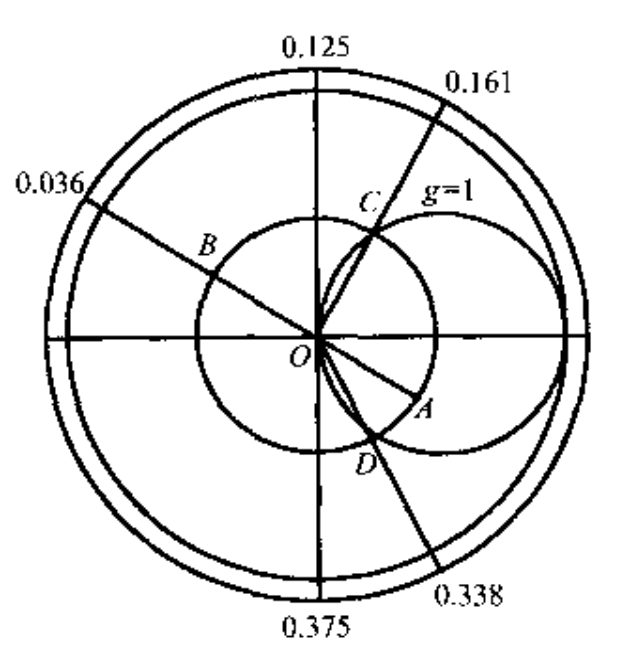
img-2024-05-07 16-12-31.png

因此

然后主线和支节线的特性阻抗一样，因此不用重新归一化。对于 点，可以读出电纳为 ，因此匹配需要为 。从短路点 沿着 向源端顺时针旋转到 点，即标度为 0.375，得到

同理，对于 点可以读出电纳为 ，因此匹配需要为 。从短路点 沿着 向源端顺时针旋转到 点，即标度为 0.125，得到

综上得到两组解

例题

传输线终端负载的导纳为 ，用并联单支线进行匹配，主线和支线的特性阻抗均为 ，试分别用解析法和圆图法，求支线的位置和长度。

归一化输入导纳为

然后取实部得到

代入 负载为 ，得到

解得 。然后考察所需支节长度。

其中 为 ， 为从接入点看负载支路的电抗，其值为

代入数据得到 ，因此

圆图法。负载为 ，归一化后为

在图上画出，为 ，然后旋转 180 得到导纳点，为 ，对应标度约为 。然后找与 的交点 ，其角度约为 ，对应标度应该分别为 和 ，因此

然后求出这两个点的电纳。在图中读出两个点的归一化电纳约为 。在圆图中，从短路点 向源端顺时针旋转，从 一直旋转到

在圆图中，从短路点 向源端顺时针旋转，从 一直旋转到

Interactive Graph
Table Of Contents
单支节匹配
计算
解析法
图解法
例题
例题
例题