Smith 圆图
(每年考试必考)
「Smith 圆图」(Smith Chart)是均匀传输线理论中一种可视化的描述某个阻抗的方法,任何一个阻抗都可以在 Smith 圆图中表示。
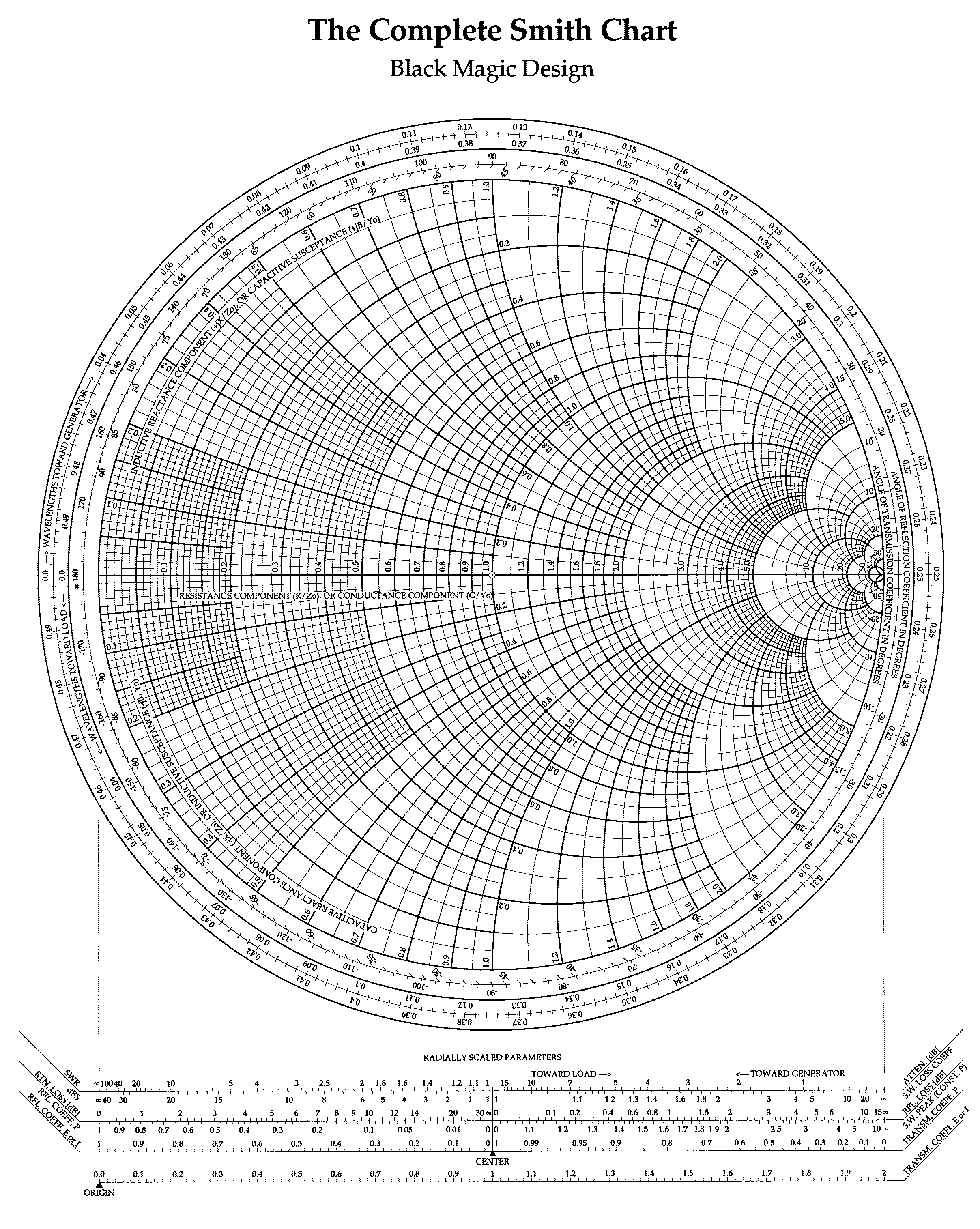
Smith 圆图可以描述某个阻抗相对于特性阻抗的关系,从而帮助匹配。
理论基础
1. 归一化思想
为了理解 Smith 圆图,首先要理解两个基本思想。
Smith 圆图希望在一张图里表示所有情况,涉及到了两个归一化。为了表示某个阻抗与特性阻抗的相对关系,将需要表示的阻抗除以特性阻抗,从而定义「归一化输入阻抗」为
2. 组成
为了理解 Smith 圆图,我们先来讨论它是怎么一步步画出来的。
2.1 反射系数
首先,建立一个
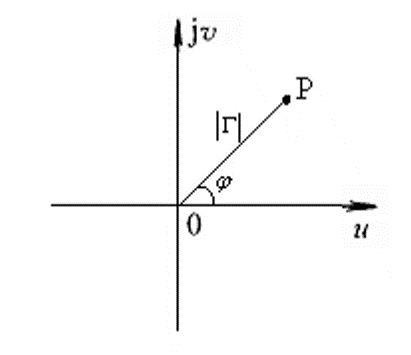
对于一个确定的系统,其反射系数的模是系统的不变量,但相位是频率的周期量。以
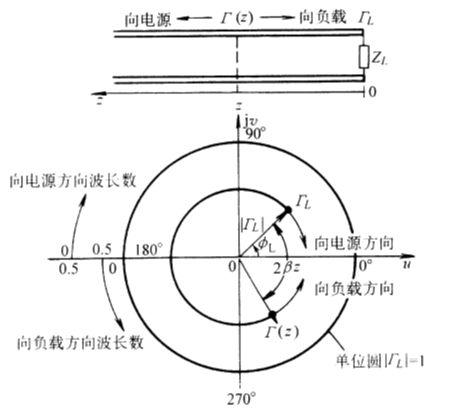
由于
2.2 等电阻圆
由于归一化后的输入阻抗可以表示为
令
进行分母有理化,得到
得到
整理得到
可见,当归一化电阻
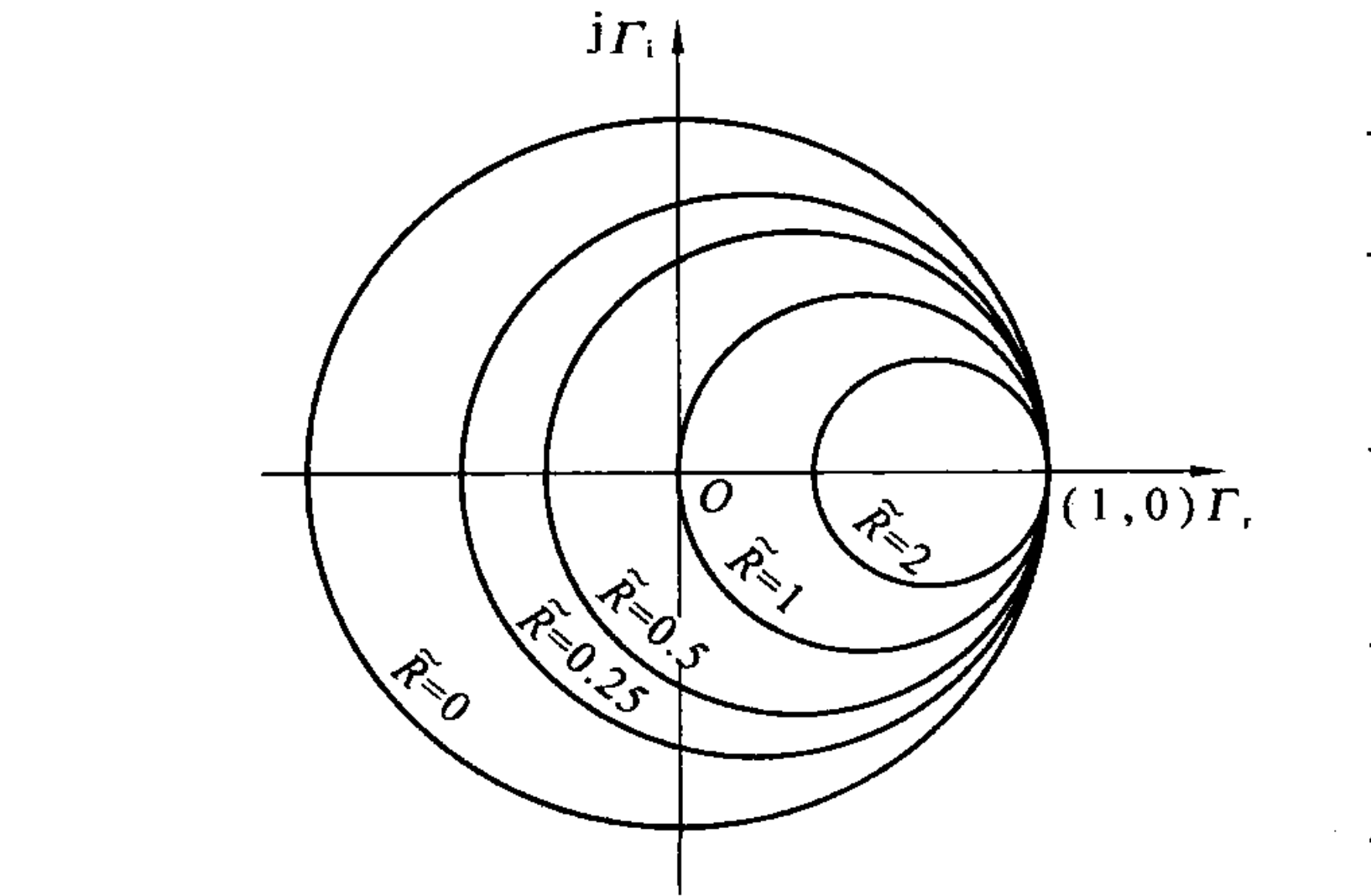
称得到的一系列圆为「等电阻圆族」。
可以得到两个重要结论
类似的,也有一系列等电导圆。如果从电导的角度来说,此时的短路点反而是最右侧,开路点是最左侧。
2.3 等电抗圆
同理,对虚部通过数学运算可以得到
整理得到
可见,当归一化电抗
不难发现,当电抗呈感性时,它分布在上半圆,而电抗呈容性时分布在下半圆。特别的,当
取一些
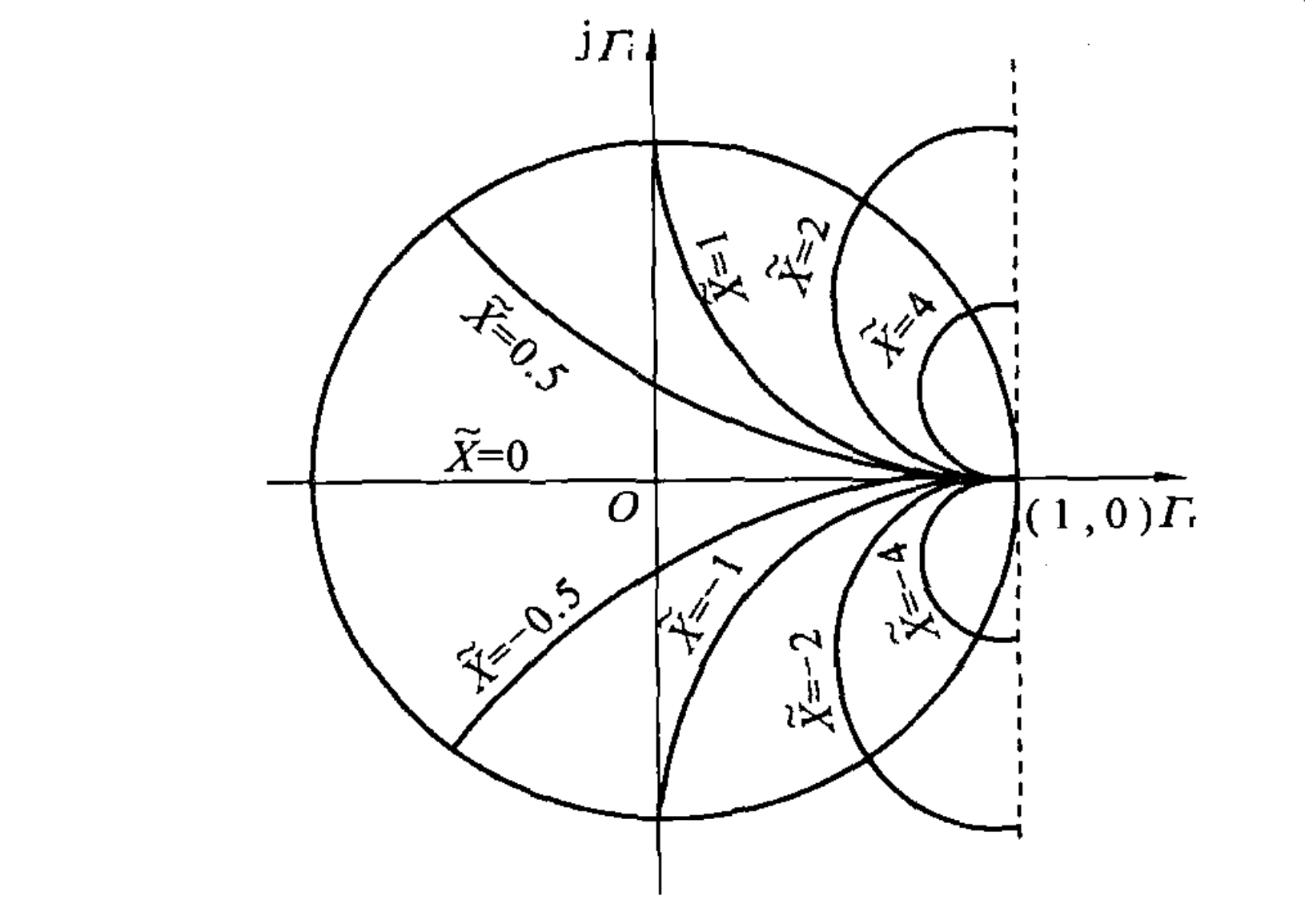
称得到的一系列圆为「等电抗圆族」。将许多等电阻和等电抗图叠加起来,就得到了 Smith 圆图

如上图,在横轴上的数字对应了一组组等电阻圆的归一化电阻值,而外侧等电抗圆的写着的数字对应了归一化电抗值。
圆图最外侧则写出了个个点的电角度和长度。由于在均匀传输线中,各种参数都呈现
内圈则表示的是角度。在已知反射系数求阻抗时,可以根据反射系数的模画出等反射系数圆,根据其相角找到对应的角度,即可在图中确定唯一的点,然后读电阻圆和电抗圆即可读出阻抗
由于等电抗圆中有一个特殊条件:当
- 横轴最左侧,对应了阻值为零,即短路
- 原图中心点,对应归一化电阻为 1,即与特性阻抗相等,实现匹配。这是我们希望追求的目标
- 横轴最右侧,对应了阻值为无穷大,即开路
2.4 归一化导纳
归一化导纳定义为
注意到
因此得到
从 Smith 圆图上来说,将归一化阻抗点旋转 180°,可得归一化导纳。在使用 Smith 圆图进行读数时,需要时时刻刻理清楚现在是在使用阻抗还是使用导纳。
3. 基本功能
因此,对于任何形式的负载,都可以在归一化之后在 Smith 圆图中找到自己的位置。此时 Smith 圆图就可以类似查表,帮助我们解决问题。
Smith 圆图能解决的问题,可归纳为四类基本问题
3.1 已知阻抗求导纳
已知阻抗
解:
首先进行归一化
反归一化
3.2 已知阻抗求反射系数,驻波比
已知
解:
在图上读出来即可
3.3 已知负载和电角度,求输入阻抗
已知
解:
首先归一化,
3.4 已知
已知
解:对于行驻波,
得到电压波节点处的阻抗为
在此题目中·,利用结论得到
在 Smith 圆图中,根据
为了求出负载阻抗,只需要逆时针旋转