Bayes 网络
「贝叶斯网络」(Bayesian Network),又被称为贝叶斯「信念网络」(Belief Network)、因果网络,起源于贝叶斯统计分析。贝叶斯网络将因果知识和概率知识相结合的信息表示框架,使得不确定性推理在逻辑上变得清晰,理解性更强。贝叶斯网络将概率论与数理统计和图论相结合,利用图结构描述随机变量之间的依赖关系。贝叶斯最早由 Judea Pearl 于 1986 年提出,并逐渐发展起来,主要用于表示不确定性知识和推理问题。
贝叶斯网络已经成为数据库中知识发现和决策支持系统的有效方法:从大量数据中构造贝叶斯网络模型,从而进行不确定性知识的发现。
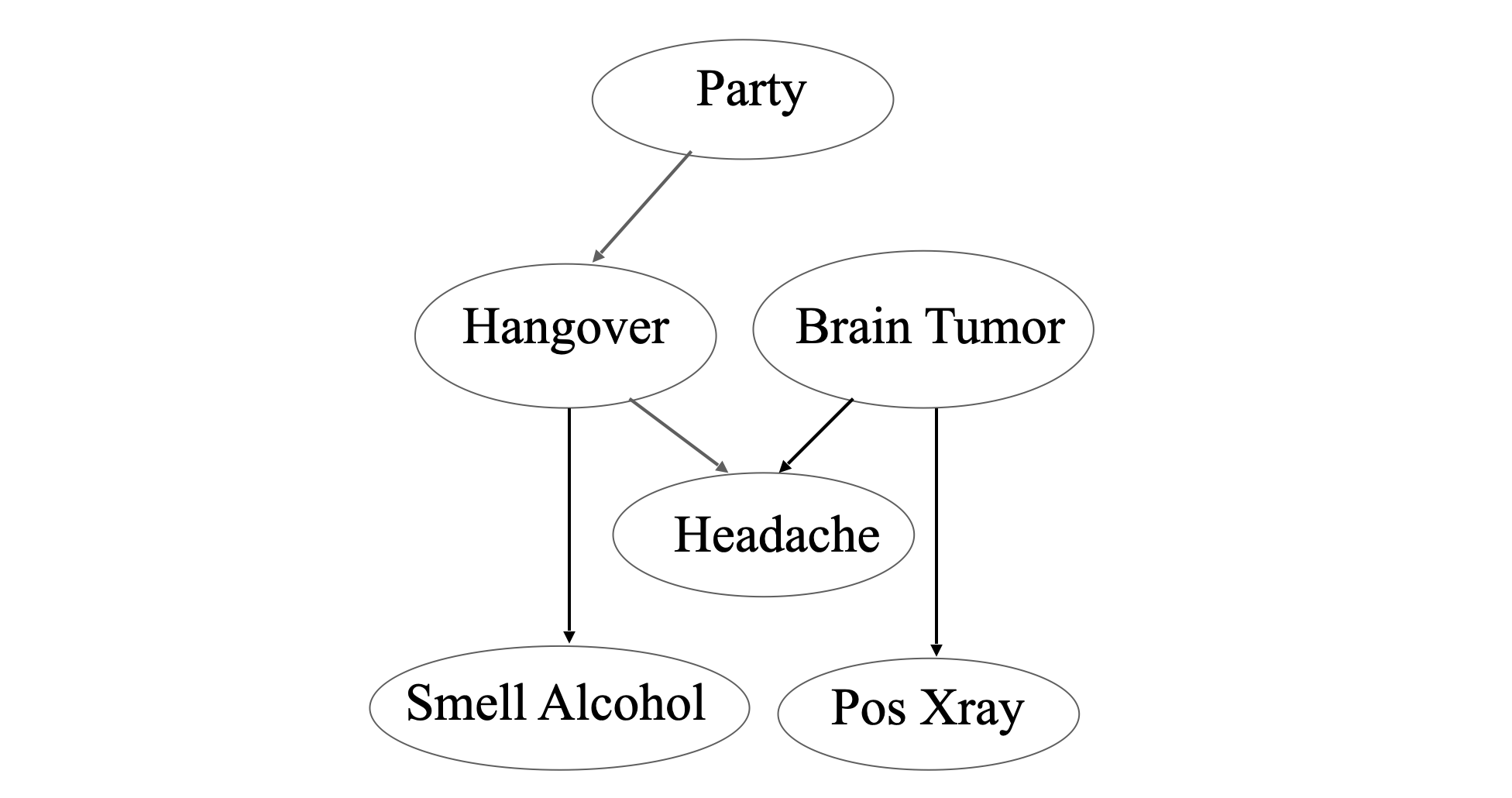
如图所示贝叶斯网络包含 6 个节点:
- 参加晚会 (Party, PT)
- 宿醉 (Hangover, HO)
- 患脑瘤 (Headache, HA)
- 头疼 (Brain tumor, BT)
- 有酒精味 (Smell alcohol, SA)
- X 射线检测呈阳性 (Pos Xray, PX)
想想这样一个场景,一个中学生回家后,其父母猜测她参加了晚会,并且喝了酒,第二天这个学生感到头疼,它的父母带她到医院做头部的 X 光检查。经过长期的观察,或者从别人那里了解,这个中学生的父母知道他们的女儿参加晚会的概率。经过长时间的数据积累,他们也知道他们的女儿参加晚会后宿醉的概率。因此,节点 party 和节点 hangover 之间有一条连线。同样,有明显的因果关系或相关关系的节点之间都有一条连线,并且连线从原因节点出发,指向结果节点。
- 如果父母已知他们的女儿参加了晚会,那么第二天一早,她呼出的气体中有酒精味的概率有多大?也就是说,当 party 发生时,smell alcohol 发生的概率有多大?
- 如果他们的女儿头疼,那么她换患脑瘤的概率有多大?这时,如果它们又知道昨晚她参加了晚会,那么综合这些情况,她换脑瘤的可能性有多大?
- 如果父母早晨闻到女儿呼出的气体有酒精味,那么她昨晚参加晚会的概率有多大?
贝叶斯网络借助于有向无环图(Directed Acyclic Graph,DAG)来刻画属性之间的依赖关系,并用「条件概率表」(Conditional Probability Table,CPT)来描述属性的联合分布。
贝叶斯网络
- 结构
- 参数
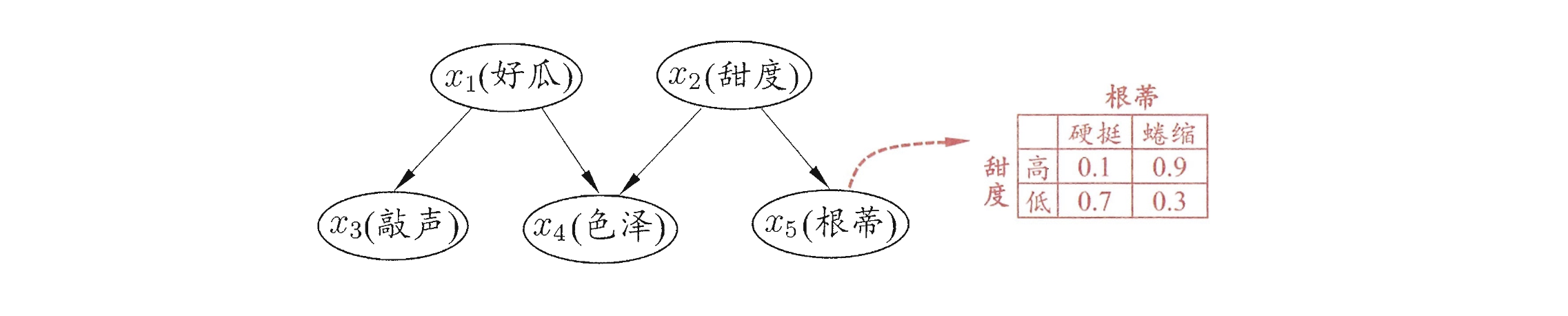
贝叶斯网络有效地表达了属性间的条件独立性。给定父节点集合,贝叶斯网络假设每个属性与它的非后裔属性独立,于是

- 「同父结构」:给定父节点
- 「顺序结构」:给定
- 「V 型结构」:给定子节点
道德图
评分函数
训练
贝叶斯网络的建立
- 首先,要把实际问题中的事件抽象为网络中的节点,每个结点必须由明确的意义,至少有是、非两个状态或多个状态,并且这些状态在概率意义上式完备的和互斥的。也就是说,所有状态在某一时刻只能发生一个,并且这些状态的概率之和为 1
- 其次,在两个或多个结点之间建立连线。基本原则:
- 有明确因果关系的节点之间应建立连线
- 没有明确因果关系的结点之间尽量不要建立连线,以防止网络过于复杂而不能把握问题的本质。
- 可采用相关性分析方法,如Pearson 相关系数来确定节点之间是否应该有连线
- 在两个节点之间建立连线时,要防止环的出现,因为贝叶斯网络必须是无环图。
贝叶斯网络的「训练」指学习得到节点的概率分布和结点间的条件概率分布的过程。可以通过专家经验填入,但是用的方法更多是通过历史数据训练得到。
例如给出训练数据
| Sample | PT | HO | BT | HA | SA | PX |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 0 | 0 | 0 | 0 | 0 |
| 4 | 1 | 1 | 1 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 1 |
| 6 | 1 | 1 | 0 | 1 | 1 | 0 |
| 7 | 1 | 0 | 1 | 0 | 1 | 0 |
| 8 | 0 | 0 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 0 | 1 | 0 |
| 10 | 1 | 1 | 1 | 1 | 1 | 1 |
可以用统计的方式得到任意节点的概率分布。假设结点
如果
其中,
同理,可以计算出多个结点间的联合条件分布。假设
其中
如果某个节点是结果节点或中间节点,那么得到这个节点的概率分布的方式有如下两种
- 直接从训练数据集中通过统计获得
- 先从表格数据中通过统计获得原因结果的概率分布,再从训练数据集中通过统计获得条件概率分布或联合条件概率分布。最后用全概率公式计算中间节点或结果节点的概率分布。
可以验证,这两种方式获得的概率分布是一致的。
贝叶斯网络是一种概率推理技术,结合概率推论和图结构来描述不同只是成分之间的条件而产生的不确定性。
贝叶斯网络的学习,是利用现有数据对先验知识进行修正的过程,每一次学习都对贝叶斯网络的先验概率进行调整,使得新的贝叶斯网络更能反映数据中蕴含的知识。贝叶斯网络能够持续学习,上次学习得到的后验贝叶斯网络编程下一次学习的先验贝叶斯网络,每一次学习前用户都可以对先验贝叶斯网络进行调整,使得新的贝叶斯网络更能体现数据中蕴含的知识。
应用
基于训练数据集构建了贝叶斯网络后,可进行预测和诊断。
例题
给出下图的 Bayes 网络
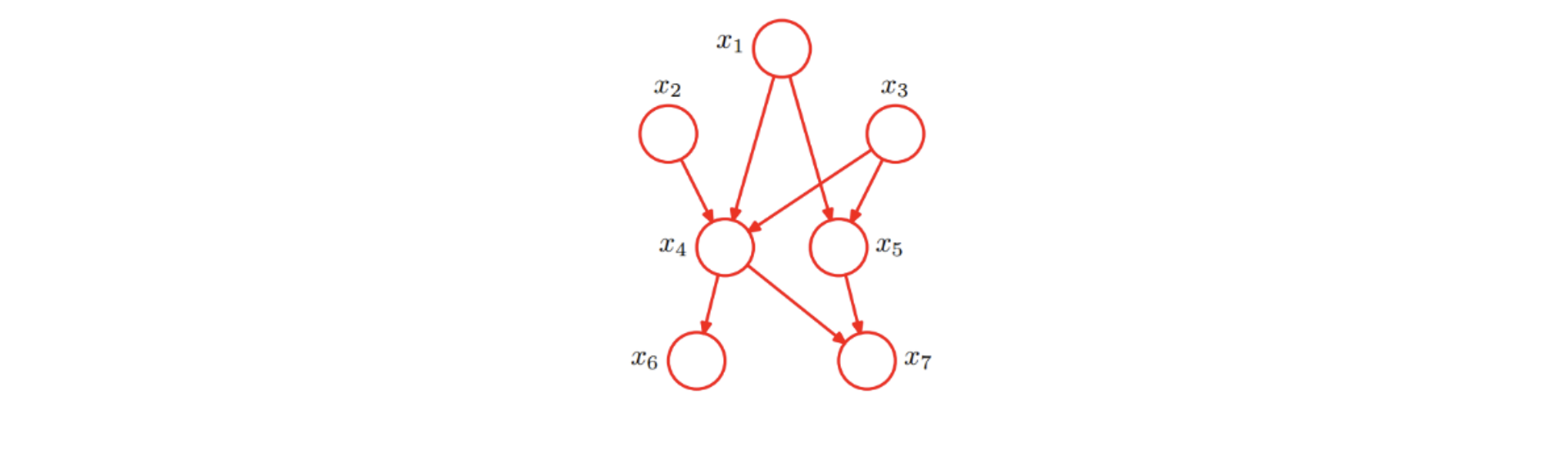
- 写出
解:
由 Bayes 网络可以直接写出
由图可知
例题
下图给出了表中的的数据集对应的贝叶斯信念网络(假设所有的属性都是二元的)
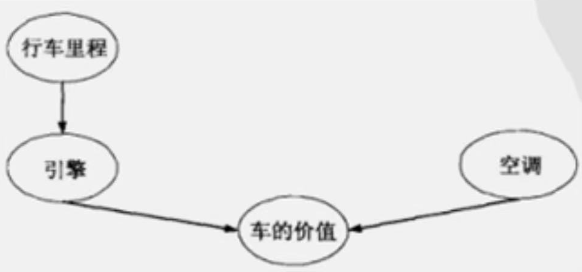
数据为
| 行车里程 | 引擎 | 空调 | 车的价值为高个数 | 车的价值为低个数 |
|---|---|---|---|---|
| 高 | 好 | 可用 | 3 | 4 |
| 高 | 好 | 不可用 | 1 | 2 |
| 高 | 差 | 可用 | 1 | 5 |
| 高 | 差 | 不可用 | 0 | 4 |
| 低 | 好 | 可用 | 9 | 0 |
| 低 | 好 | 不可用 | 5 | 1 |
| 低 | 差 | 可用 | 1 | 2 |
| 低 | 差 | 不可用 | 0 | 2 |
- 画出网络中每个结点对应的概率表
- 使用贝叶斯网络计算
引 擎 差 , 空 调 不 可 用
解:
第一题,对于行车里程节点,概率表为
| 行车里程高 | 行车里程低 |
|---|---|
对于空调
| 空调可用 | 空调不可用 |
|---|---|
对于引擎
| 引擎好 | 引擎差 | |
|---|---|---|
| 行车里程高 | ||
| 行车里程低 |
对于车的价值
| 引擎好,空调可用 | 引擎差,空调可用 | 引擎好,空调不可用 | 引擎差,空调不可用 | |
|---|---|---|---|---|
| 车的价值高 | ||||
| 车的价值低 |
第二题,计算
然后根据引擎节点的概率表
因此