Bayes 网络预测
「贝叶斯网络预测」是指从起因推测一个结果的推理,也称为由顶向下的推理。目的是由原因推出结果。已知一定的原因,利用贝叶斯网络的推理计算,求出由原因导致的结果发生的概率。
假设Bayes 网络已经训练完毕
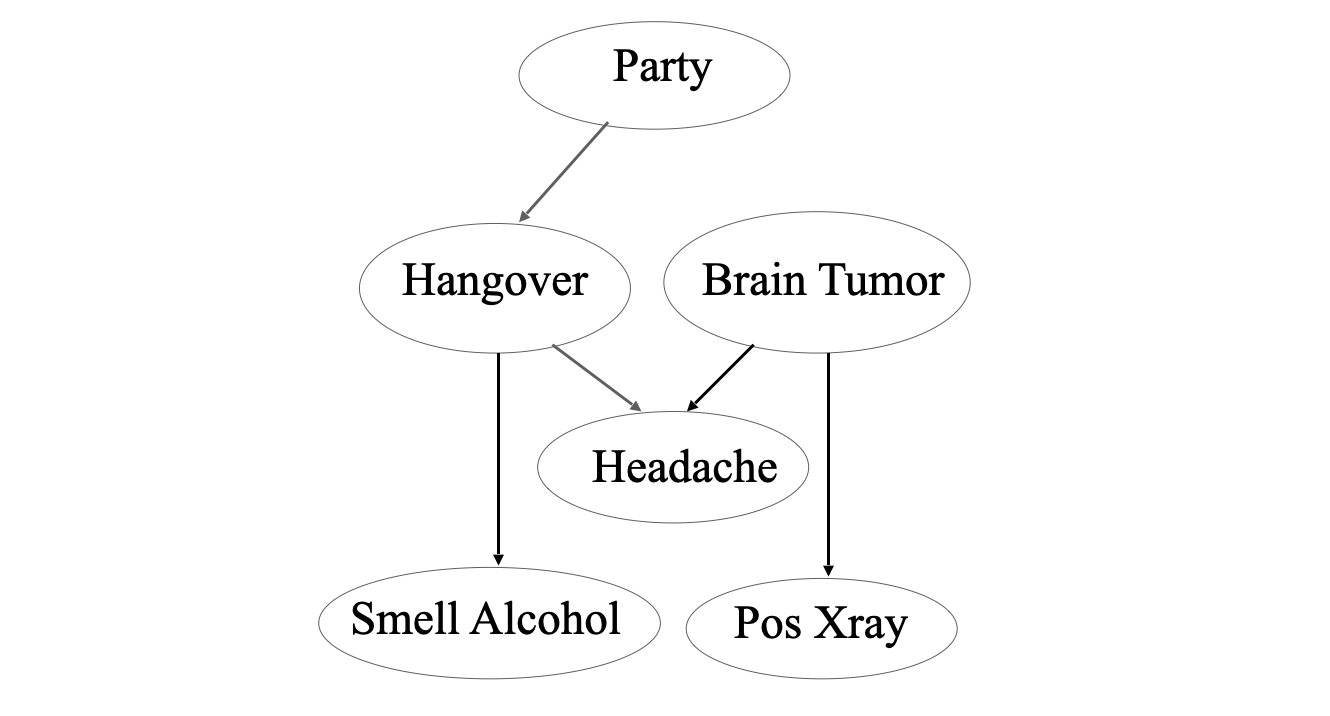
图中 Party 和 Brain Tumor 两个结点是原因节点,没有结点以它们为终点。它们的无条件概率如下表所示
| True | 0.200 | 0.001 |
| False | 0.800 | 0.999 |
该表给出了两个事件发生的概率:第二列是关于 Party 的概率:参加的概率是 0.2,不参加的概率是 0.8。第三列是关于患脑癌的概率:患脑癌的概率为 0.001,不患脑癌的概率为 0.999。
同理可以得到一系列条件概率
已知节点 PT 时 HO 的条件概率
| True | 0.7 | 0 |
| False | 0.3 | 1 |
已知节点 HO 时 SA 的条件概率
| True | 0.8 | 0.1 |
| False | 0.2 | 0.9 |
已知节点 BT 时 PX 的条件概率
| True | 0.98 | 0.01 |
| False | 0.02 | 0.99 |
得到已知 HO 时 HA 的概率为
| True | 0.99 | 0.7 | 0.9 | 0.02 |
| False | 0.01 | 0.3 | 0.1 | 0.98 |
贝叶斯网络的功能之一就是在已知某些条件节点的条件下,预测结果节点的概率。贝叶斯网络也可以在不知道任何节点信息的情况下计算某个结果节点的发生概率。图中,如果不知道任何节点发生与否的信息,仍然可以估算节点 HA 的概率。
约定,对于一个结点 Point,Point 发生的概率,
例如,有贝叶斯网络图可知,HA 与 HO 和 BT 有关,而 HO 与 PT 有关。因此首先由 HO 对应的概率,由全概率公式有
在没有任何节点信息的情况下,头疼的概率为 0.116,不头疼的概率为 0.884。用同样的方式,可以计算所有节点的概率这样可以进一步完善贝叶斯网络。事实上,完善节点概率也是预测贝叶斯网络的一种情况,即在不知道节点明确证据下的预测。
例 2
同样的,还可以计算已知参加晚会的情况下,第二天早晨呼吸有酒精味的概率
| True | 0.7 | 0.01 |
| False | 0.3 | 0.99 |
由贝叶斯网络图可以看出 SA 发生的概率只与 HO 有关,而 HO 与是否参加 Party 有关。现在已知参加了 Party,由前面的条件概率表可知,
例3
此外,还可以求出已知参加晚会的情况下,头疼发生的概率。
由贝叶斯网络图可知,HA 发生的概率与 HO 和 BT 有关。而 HO 与是否参加 Party 有关。现在已知参加了 Party,由前面的条件概率表可知
以及
也就是说,如果知道已经参加了晚会,而没有其他方面的任何证据,则这个人头痛的概率是
由此可以归纳出贝叶斯网络预测算法的步骤:
输入:给定贝叶斯网络
- 把证据向量输入到贝叶斯网络
- 对
- 如果父节点中有一个没有处理过,则不处理这个节点;否则,继续下面的步骤
- 根据节点
- 重复上述步骤,共
分类
假定有
最大化