负载阻抗 ，此时终端反射系数

驻波系数 ，此时传输线上任意点 处的反射系数为 可得

设 ，考虑到时间因子 ，则传输线上电压，电流瞬时表达式为

此时传输线上任意一点 处的输入阻抗为

传输线上任意一点 处的反射系数为

下图给出了终端短路时沿线电压、电流瞬时变化的幅度分布以及阻抗变化的情形。

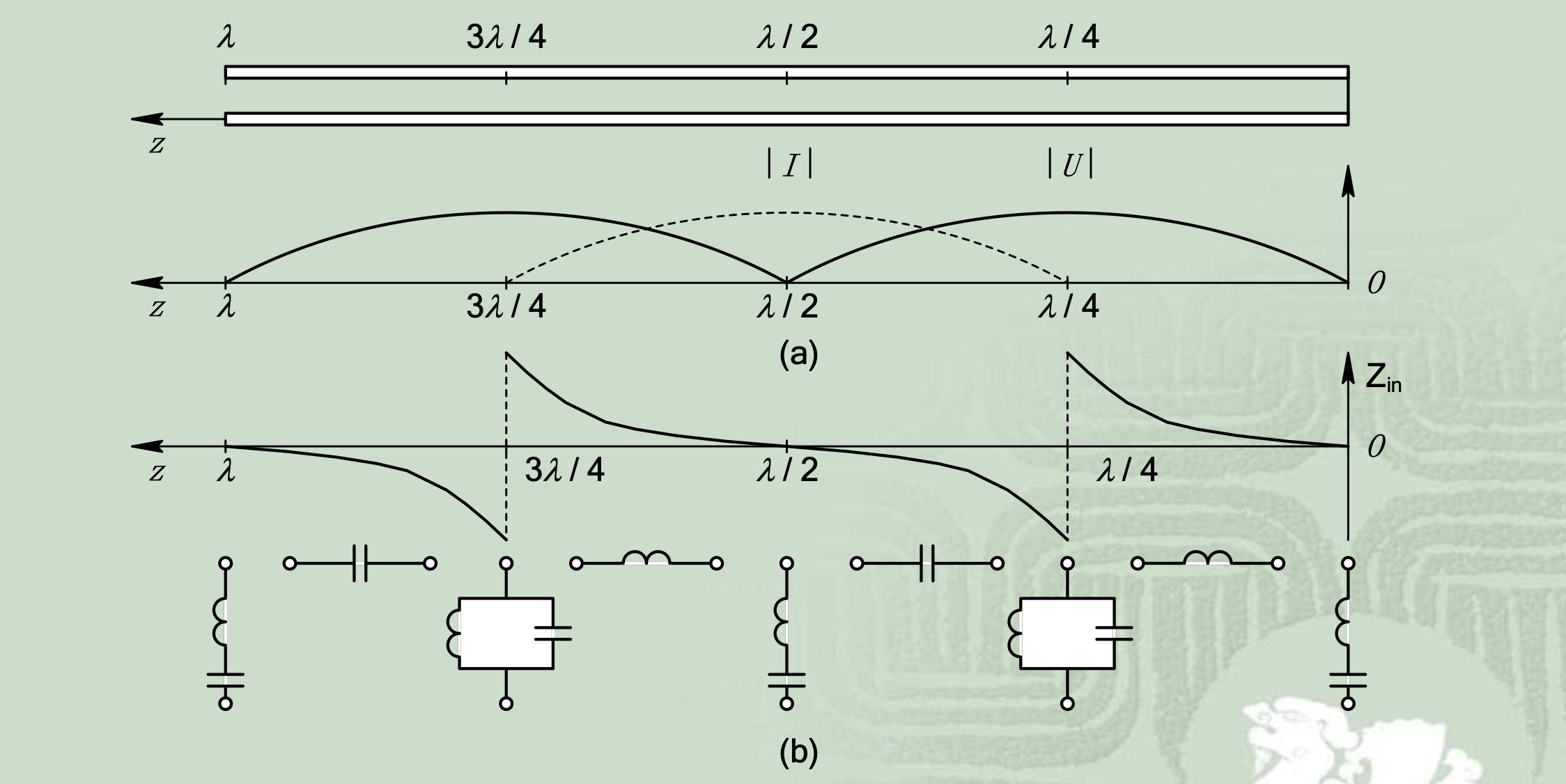
对无耗传输线终端短路情形，有以下结论

1. 沿线各点电压和电流振幅按余弦变化，电压和电流相位相差 ，功率为无功功率，即无能量传输，因此只能存储能量
2. 在 处电压为零，电流振幅最大且等于 ，称这些位置为「电压波节点」，在 处电压的振幅值最大，且等于 ，而电流为零，称这些位置为「电压波腹点」
3. 传输线上各点阻抗为纯电抗，在电压波节点处 ，相当于串联谐振，在电压波腹处 ，相当于并联谐振。在 ，在电压波腹处 ，相当于并联谐振，在 内， 相当于一个纯电感，在 内， 相当于一个纯电容，从终端起每隔 阻抗性质就变换一次，这种特性称为「 阻抗变换性」
4. 根据 ，任意的电抗性负载可用有限长度的短路线的输入阻抗来等效，因此可以用长度为 的短路线代替电抗性元件。

负载阻抗 ，终端电流 ，此时，线上任意位置的电压和电流复振幅表达式为

输入阻抗为

反射系数为

驻波系数为

电压和电流的瞬时值可以表示为

根据上述分析结果，开路线电压、电流复振幅、输入阻抗分布图如下：

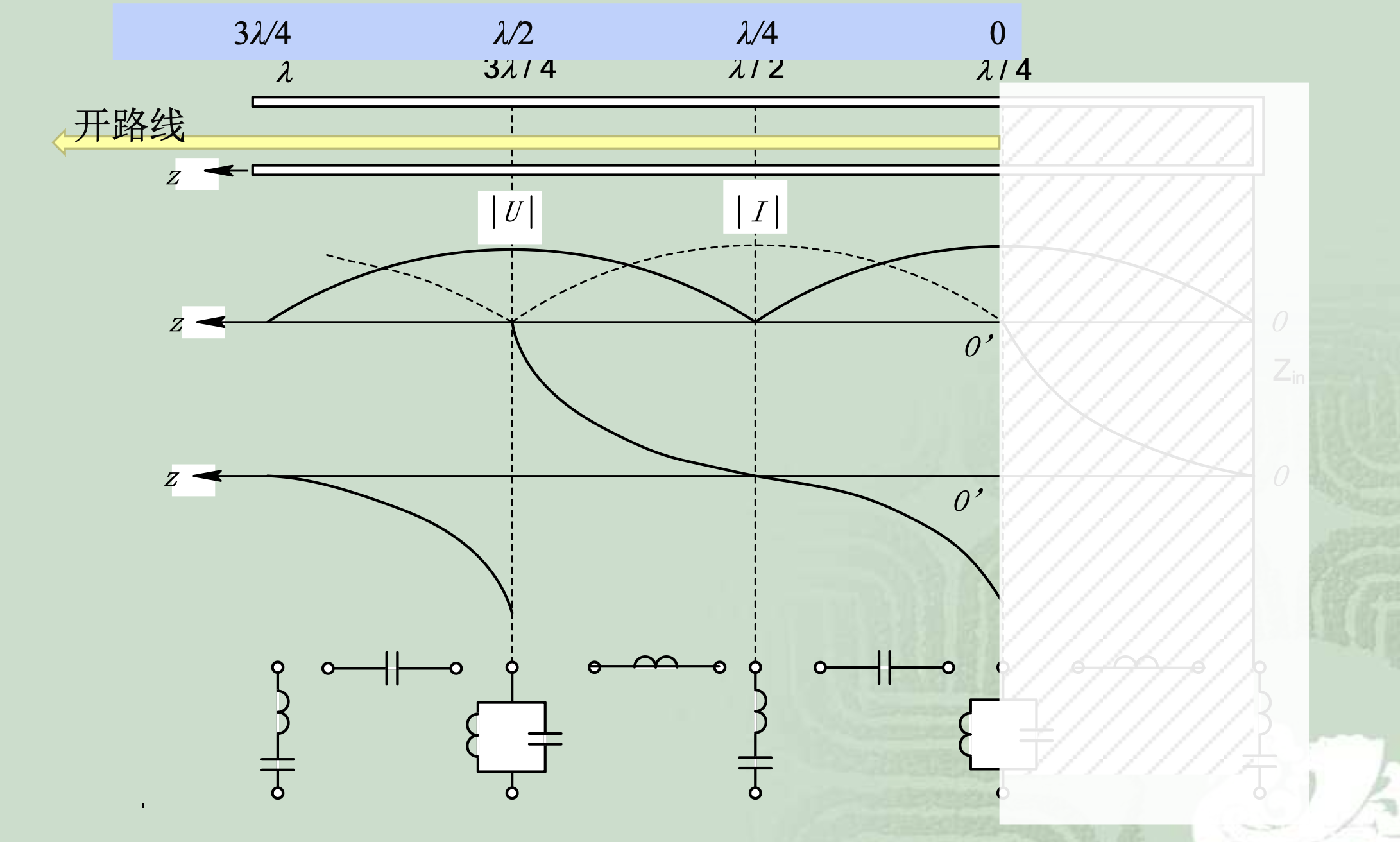
分析：终端开路时传输线上的电压和电流也呈纯驻波分布，因此也只能存储能量而不能传输能量。在 点处为「电压波腹点」。而在 点处为「电压波节点」。实际上终端开口的传输线并不是开路传输线，因为在开口处会有辐射，所以理想的终端开路线是在开口终端处接上 短路线来实现的。上图给出了终端开路时的驻波分布特性。 位置为终端开路处， 为 短路线

由于短路状态阻抗为

开路状态阻抗为

因此可以通过 变换来实现互相转换。

当均匀无耗传输线端接纯电抗负载 时，因负载不能消耗能量，仍将产生全反射，入射波和反射波振幅相等，但此时终端既不是波腹也不是波节，沿线电压、电流仍按纯驻波分布。由前面分析得小于 的短路线相当于一纯电感，因此当终端负载为 的纯电感时，可用长度小于 的短路线 来替代。由式 得

同理可得，当终端负载为 的纯电容时，可用长度小于 的开路线 来代替，或用长度为大于 小于 的短路线来代替，由 有

下图给出了终端接电抗时驻波分布及短路线的等效

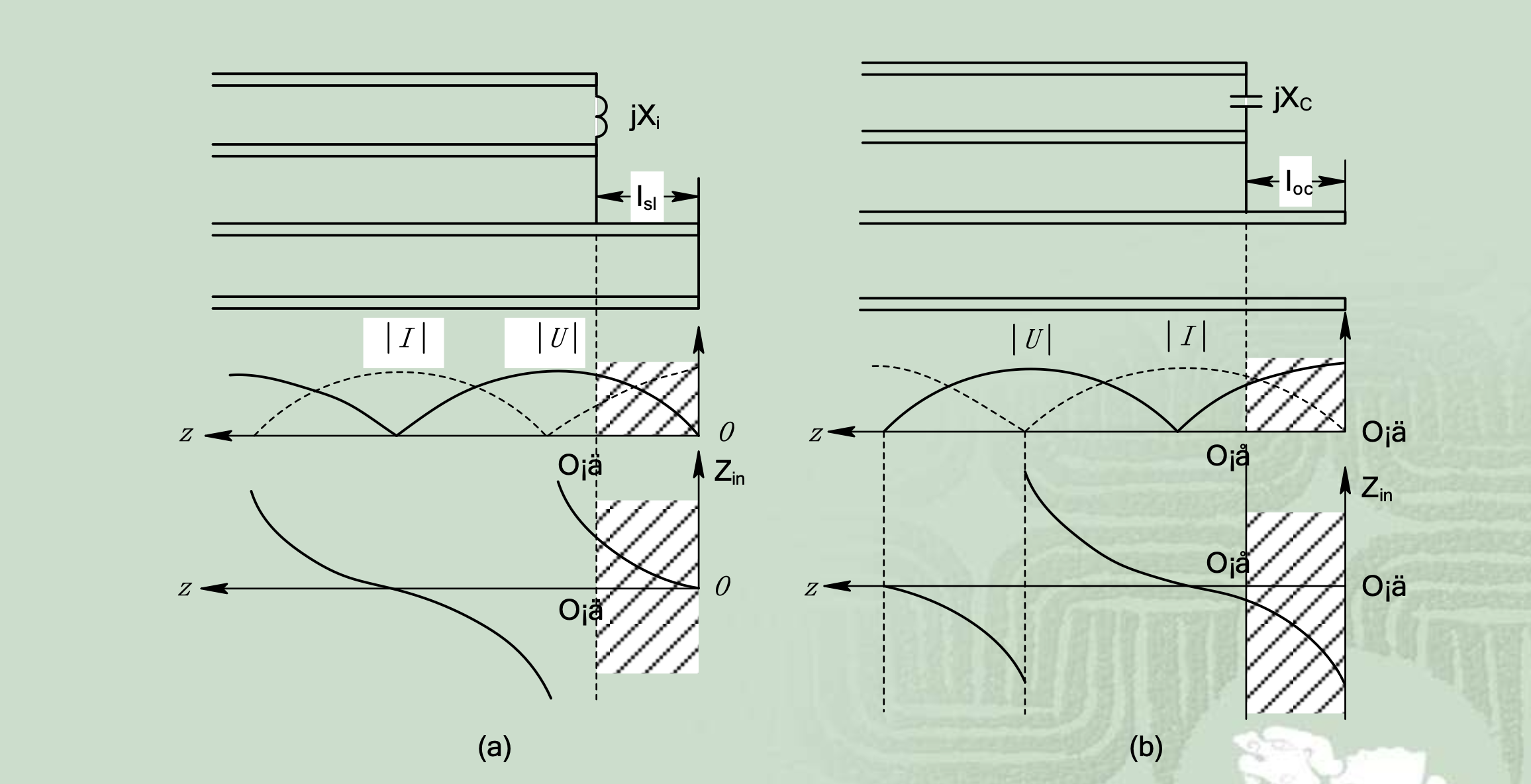
总之，纯驻波工作状态的无耗传输线，沿线各点电压、电流在时间和空间上均相差 ，故它们不能用于微波功率的传输，但因其输入阻抗的纯电抗特性，在微波技术中有着非常广泛的应用。

线圈因短路状态作为标准状态，其他状态视为短路状态移动

利用 的和角公式得到

其中

证明了任意电抗的特性阻抗，可以用短路状态进行一个平移来实现。

• ，电抗呈容性，
• ，电抗呈感性，