一、数字电路与数字信号
1. 数字技术的发展及其应用
电子技术是,20 世纪发展最迅速的技术。其中数字电子技术,广泛用于广播、电视、通信、医疗、控制、测量、交通、航空、军事、探测、文娱、家用电器等领域
1.1 电子技术发展简史
以电子器件的发展为基础。
- 1906 年,福雷斯特等发明了电子管
- 1947 年第一只晶体三极管问世,半导体技术诞生。
- 20 世纪 60 年代初,模拟和数字集成电路出现
- 之后出现现代个人计算机 CPU 和主板
1.2 电路设计方法
伴随着器件的发展,从传统走向现代。
- 传统设计方法:逻辑抽象 → 逻辑代数 → 逻辑化简 → 逻辑电路 → 电路调试
- 现代设计方法:
- EDA (Electronics Design Automation) 技术,设计软件化
- 硬件描述 → 行为仿真 → 综合 → 时序仿真 → 网表下载
- 将生成的网表数据下载到芯片,实现系统功能
2. 数字集成电路的分类及特点
电子电路按照功能,可以分为「模拟电路」和「数字电路」。而其中数字电路按照电路特点可以分为「组合逻辑电路」和「时序逻辑电路」。
数字电路的基本单元是「逻辑门电路」。而逻辑门的底层元件称为「开关器件」,如二极管、三极管等。
集成在半导体芯片上的逻辑门电路称为「数字集成电路」
3. 模拟信号与数字信号
3.1 模拟信号
模拟自然界中随时间连续变化物理量如温度、压力等的参考量称为「模拟量」。用于表示模拟量的信号叫做「模拟信号」,处理模拟信号的电子电路称为「模拟电路」。
在工程上,通常使用传感器将模拟量转化为成比例的电压或电流信号
3.2 数字信号
用数字表示某些时刻离散变化物理量的参考量称为「数字量」。用于表示数字量的信号叫做「数字信号」,处理数字信号的电子电路称为「数字电路」。
数字电路具有以下优点
- 抗干扰能力强
- 易加密
- 便于电脑处理
- 易传输
- 高保真
3.3 模拟信号转换为数字信号
模拟信号转换为数字信号一般需要四个步骤
- 采样:用采样电路,每隔一段时间采样一个信号
- 保持:用保持电路,使采样到的信号在一段时间内保持相对稳定
- 量化:得到幅值关于量化单位的整数倍,作为数字量
- 编码:用二进制代码表示量化结果
3.4 数字电路的分析与设计
已知逻辑电路,确定输出、输入之间的逻辑关系的过程叫做「数字电路分析」。这一过程是通过逻辑代数完成的。逻辑关系可以用真值表、功能表、逻辑表达式和波形图等方式来描述
已知功能要求,选择器件,设计出符合要求的逻辑电路过程叫做「数字电路设计」。传统的设计过程是通过逻辑代数逐步建模,而现代采用 EDA 硬件描述语言来进行,包括结构建模、数据流建模,行为建模
4. 数字信号的描述方法
用 0 和 1 两个符号描述的数值称为「二值数」,用 0 和 1 两个符号描述的逻辑状态称为「二值逻辑」。为了将电路状态和逻辑状态对应起来,我们在数字电路中用电平高低两个状态来对应 0 和 1 两个状态,因此存在两种对应关系
- 正逻辑:用低 L、高 H 电平分别表示 0 和 1
- 负逻辑:用低 L、高 H 电平分别表示 1 和 0
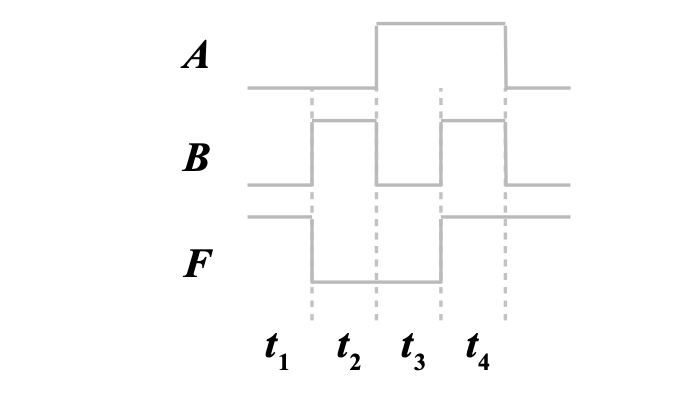
数字电路在工作时,通过电平的高低变化来传递数据。数字电路工作需要依照一定的时间间隔,一个时间间隔的逻辑状态,称为 1 位(bit),每秒钟传输数据的位数称为「比特率」。
定义脉冲宽度
5. 实际数字信号波形
在实际的电路中,波形并不是直上直下的,因此我们需要对非理想量做出相应的定义。定义脉冲的上升沿和下降沿的持续时间为脉冲的「上升时间」
定义输出信号相对于输入信号变化的延迟时间为「输出高变低电平延迟」
二、数制
1. 数制的定义
2. 十进制
3. 二进制
5. 十六进制和八进制
由于二进制书写起来较不方便,因此如果能以二的次幂进制来表示二进制码,会相对简单。由此发明十六进制数和八进制数
5.1 十六进制
位模为
我们常将 4 位二进制数转化为 1 为十六进制数来书写,如
十六进制数要转为二进制数,只需要按权展开,每位数对应四位二进制数,之后将其「拼装」起来即可
二进制数要转为十六进制数,只需要从小数点开始,划分为每四位一组,不足四位的以
5.2 八进制
位模为
八进制与二进制转换与十六进制的原理类似,在此不做赘述。
6. 互补与互反
设
若
对于二进制数而言,若
比如二进制数
三、二进制数的算术运算
1. 有符号数与无符号数
1.1 无符号数
显然,一串
1.2 有符号数
但是在实际工程中,必须处理负数,为了让二进制数也能表示负数,在之前的无符号数的基础上又发展出了「有符号数」,即将二进制数的最高位作为其符号位,
对于正数而言,
原码
有符号数中的正数的剩余
原码能表示的负数范围为
比如
但很快出现一个问题,原码表示的二进制有符号数之间的算数运算无法与十进制数相统一。还是以
反码
让负数的剩余
反码能表示的负数范围为
这样一来,就实现了有符号二进制数的运算与十进制统一。还是以
补码
让负数的剩余
补码能表示的负数范围为
2. 带符号二进制数的加法运算
2.1 减法运算
为简化运算,数字电路系统通常采用加法器进行减运算,在做减运算的同时本质上就是加上带符号二进制数的补码。即 "-" 运算符实质上是在求
因此
快速求补法:符号为
2.2 溢出
若用四位二进制带符号数运算
如何判断带符号数的溢出?首先分析两个符号相反的数相加的情况。由于符号相反,结果的绝对值必然小于两个加数,因此不可能产生溢出。对于其他情况,最高位,即符号位在运算时会可能会产生进位,称此进位数为「最高进位」,最高数值位,即次高位的进位称为「次高进位」,最后的结果称为「符号位」
可以得到下列三条法则
- 两个符号相反的数相加不会产生溢出
- 同符号数之和,最高进位与符号位相反时,产生溢出
- 最高进位和次高进位的进位相反时,产生溢出
四、二进制代码
1. 编码
数字系统中的信息可以分为两类,第一类为数值,第二类为信息符号。信息符号包括文字、控制符、事物标识等。在前面几章中重点介绍的是数值,接下来介绍用二进制代码来表示信息符号。
以一定规则编制各种信息符号的过程称为「编码」,编码所遵循的规则称为「码制」。对于
2. BCD 码
用 4 位二进制数代码对十进制的十个数字“符号”进行的码制称为「BCD 码」(Binary Code Decimal)。四位二进制代码能提供 16 种组合,给十个数字符号编码只需要选取其中的十个,不同的选择就产生了不同的 BCD 码。BCD 码可以根据其二进制数是否有权重分为「有权码」和「无权码」,常用的 BCD 码有:
- 有权码:8421 码,2421 码,5421 码
- 无权码:余 3 码,余 3 循环码
2.1 8421 码
8421 码是一种最典型的有权 BCD 码,该码由高到低四位数字分别按照 8、4、2、1 位权展开得到的多项式之和,即为该码所表示的多项式之和。如
故
8421 码最大的特点就是与二进制自然码规则类似,因此十分直观。 8421 码中不包含后 6 个 4 位自然码。
2.2 2421码
2421 码是另外一种有权码,该码由高到低四位数字分别按照 2、4、2、1 位权展开得到的多项式之和,即为该码所表示的多项式之和。为了使 2421 码唯一,规定
故
2421 码的特点是对 9 自补,即 0 和 9、 1 和 8、2 和 7、3 和 6、 4 和 5 的码各位互反。8421 码中不包中间 6 个 4 位自然码。
3. 余 3 码
余 3 码(Excess-3 code)是一种最常用的无权码,其码等于 8421 码的 4 位二进制数值加上二进制的
余 3 码的特点是对 9 自补,且进位规则与十进制类似,比如
余三码中不包含前后两端各三个 4 位自然码。下表给出了几种常见的 BCD 代码
| 十进制数 | 8421 码 | 2421 码 | 5421 码 | 余 3 码 | 余 3 循环码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 | 0010 |
| 1 | 0001 | 0001 | 0001 | 0100 | 0110 |
| 2 | 0010 | 0010 | 0010 | 0101 | 0111 |
| 3 | 0011 | 0011 | 0011 | 0110 | 0101 |
| 4 | 0100 | 0100 | 0100 | 0111 | 0100 |
| 5 | 0101 | 1011 | 1000 | 1000 | 1100 |
| 6 | 0110 | 1100 | 1001 | 1001 | 1101 |
| 7 | 0111 | 1101 | 1010 | 1010 | 1111 |
| 8 | 1000 | 1110 | 1011 | 1011 | 1110 |
| 9 | 1001 | 1111 | 1100 | 1100 | 1010 |
2. 格雷码
接下来介绍一种典型的二进制代码,「格雷码」(Gray Code)。与二进制码类似,格雷码也是用于表示十进制数的代码,但两组相邻码之间只有一位不同。这种编码规则可以防止代码变化过程中由于电子器件变化速度不一致而产生短暂错误码。一组典型的格雷码可以表示为
| 十进制数 | 二进制码 | Gray码 |
|---|---|---|
| 0 | 0000 | 0000 |
| 1 | 0001 | 0001 |
| 2 | 0010 | 0011 |
| 3 | 0011 | 0010 |
| 4 | 0100 | 0110 |
| 5 | 0101 | 0111 |
| 6 | 0110 | 0101 |
| 7 | 0111 | 0100 |
| 8 | 1000 | 1100 |
| 9 | 1001 | 1101 |
| 10 | 1010 | 1111 |
| 11 | 1011 | 1110 |
| 12 | 1100 | 1010 |
| 13 | 1101 | 1011 |
| 14 | 1110 | 1001 |
| 15 | 1111 | 1000 |
2.1 格雷码-二进制码转换
格雷码到二进制码
格雷码的最高位与二进制码最高位相等,其余各位等于二进制码的对应位与其高一位做「异或」,即“不同取 1,相同取 0”。异或的具体定义在之后会介绍。用公式表示为
例如
二进制码到格雷码
二进制码的最高位与格雷码最高位相等,其余各位等于格雷码的对应位与二进制码的对应高一位做「异或」,用公式表示为
例如
注:异或运算参见下一部分《二值逻辑变量与基本逻辑运算》
3. ASCII 码
除了对十进制数和二进制数编码,还可以对任意字母和符号编制代码,称这样的代码为「字符代码」,其中最经典的就是美国信息交换标准代码( American Standard Code for Information Interchange),即「ASCII 码」。ASCII 码共有 128 个代码,可表示英文字母、阿拉伯数字、标点符、
运算符、控制符等,普遍用于键盘指令和文本数据。
五、二值逻辑变量与基本运算
1. 基本逻辑
1.1 与
AND
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
其 ANSI/IEEE 通用符号为
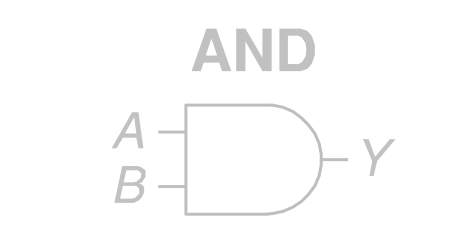
ISO / IEC 国标符号为
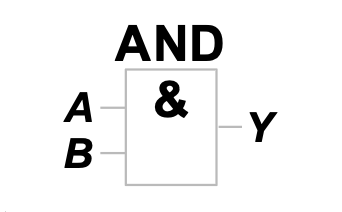
1.2 或
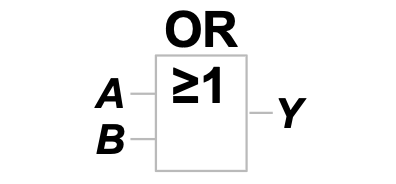
OR
Y=A+B
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
其 ANSI/IEEE 通用符号为
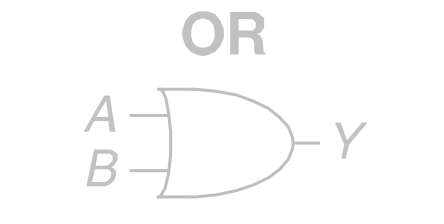
ISO / IEC 国标符号为
1.3 非
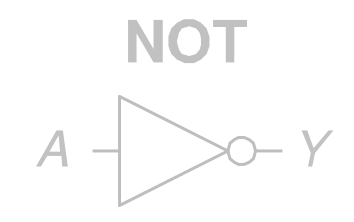
NOT
Y=\overline{A}
其真值表为
| A | Y |
|---|---|
| 0 | 1 |
| 1 | 0 |
其 ANSI/IEEE 通用符号为
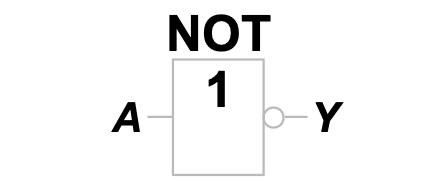
ISO / IEC 国标符号为
2. 其他逻辑运算
2.1 与非
NAND
是与运算和非运算的复合
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
其 ANSI/IEEE 通用符号为
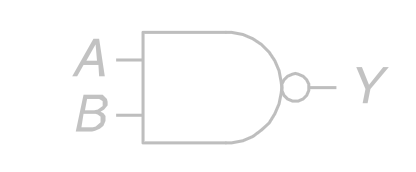
ISO / IEC 国标符号为
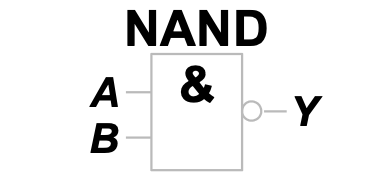
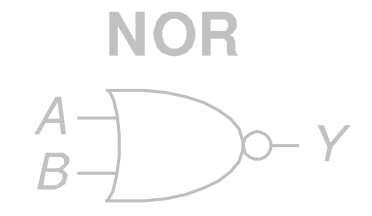
2.2 或非
NOR
是或运算与非运算的复合
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
其 ANSI/IEEE 通用符号为
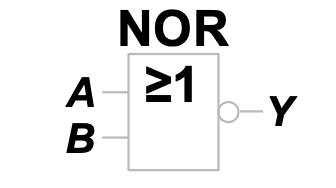
ISO / IEC 国标符号为
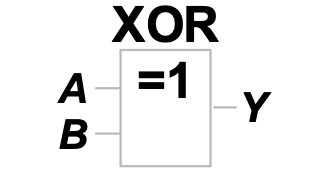
2.3 异或
XOR
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
其 ANSI/IEEE 通用符号为
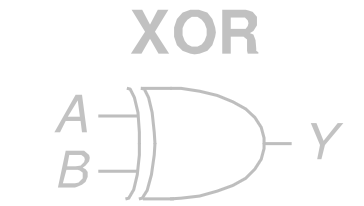
ISO / IEC 国标符号为
2.4 同或
XNOR
其真值表为
| A | B | Y |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
其 ANSI/IEEE 通用符号为
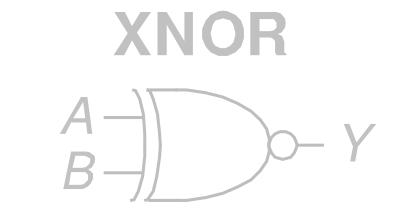
ISO / IEC 国标符号为
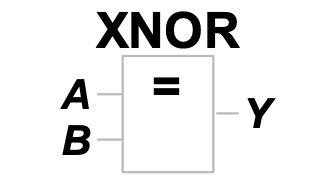
可用真值表、逻辑函数表达式、逻辑图、波形图和卡诺图描述输入和输出的逻辑关系。
六、逻辑函数及其表示方法
1. 真值表
输入变量所有取值组合与函数值间的对应关系列成表格。例如同或逻辑可以表示为
| A | B | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. 逻辑表达式
例如同或逻辑可以表示为
3. 逻辑图
例如同或逻辑可以表示为
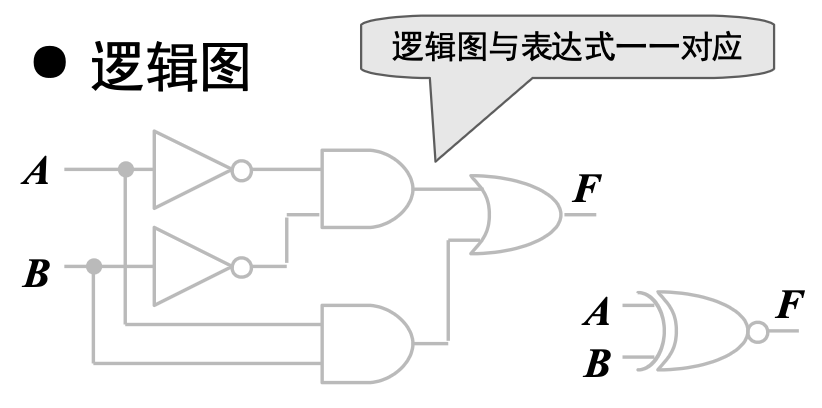
4. 波形图