一、前言
在模拟电路中,存在许多电容,包括耦合电容(看得见的电容)和三极管的结电容(看不见的电容)。之前对于电容的分析通常非常简单粗暴,在交流分析中视为短路,直流分析中视为开路,从不考虑频率。
但在某些电路中,会有放大指定频率的需求。比如某音响放大电路,需要放大频率为
二、基础概念
1. 贝和分贝
「贝尔」(Bell)是量度两个相同单位之数量比例的计量单位,记为
其中
在实际应用中,1 贝尔相当于两信号的能量相差十倍,相差过大使用不便,因此通常用「分贝」来替代「贝」,记为
比如
2. 通带
在频幅响应曲线上,相较于最大频幅相差
根据定义,在频率上限和下限,功率为最大功率的一半,那么根据
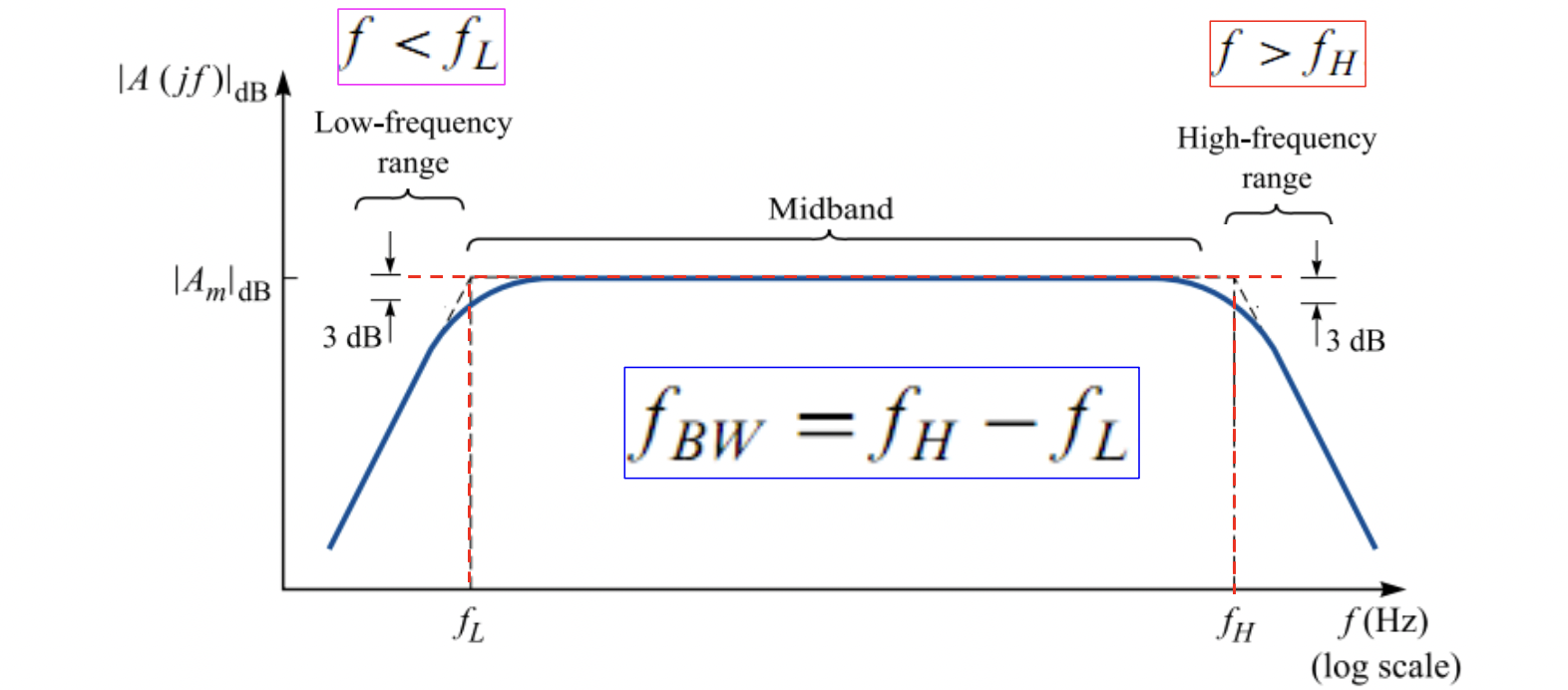
频率上限和下限就是信号幅度较大的频率范围。我们称频率上限和下限之间的频率范围为「通带」,频率上限和下限之差为,简称「带宽」(Bandwidth),公式为
由于
三、等效电路
对于一般的三极管放大电路,根据之前的知识,在不考虑任何电容的情况下,其电压增益为
现在考虑真实的电路。一般的三极管放大电路如下图,包括了输入/输出端的耦合电容(
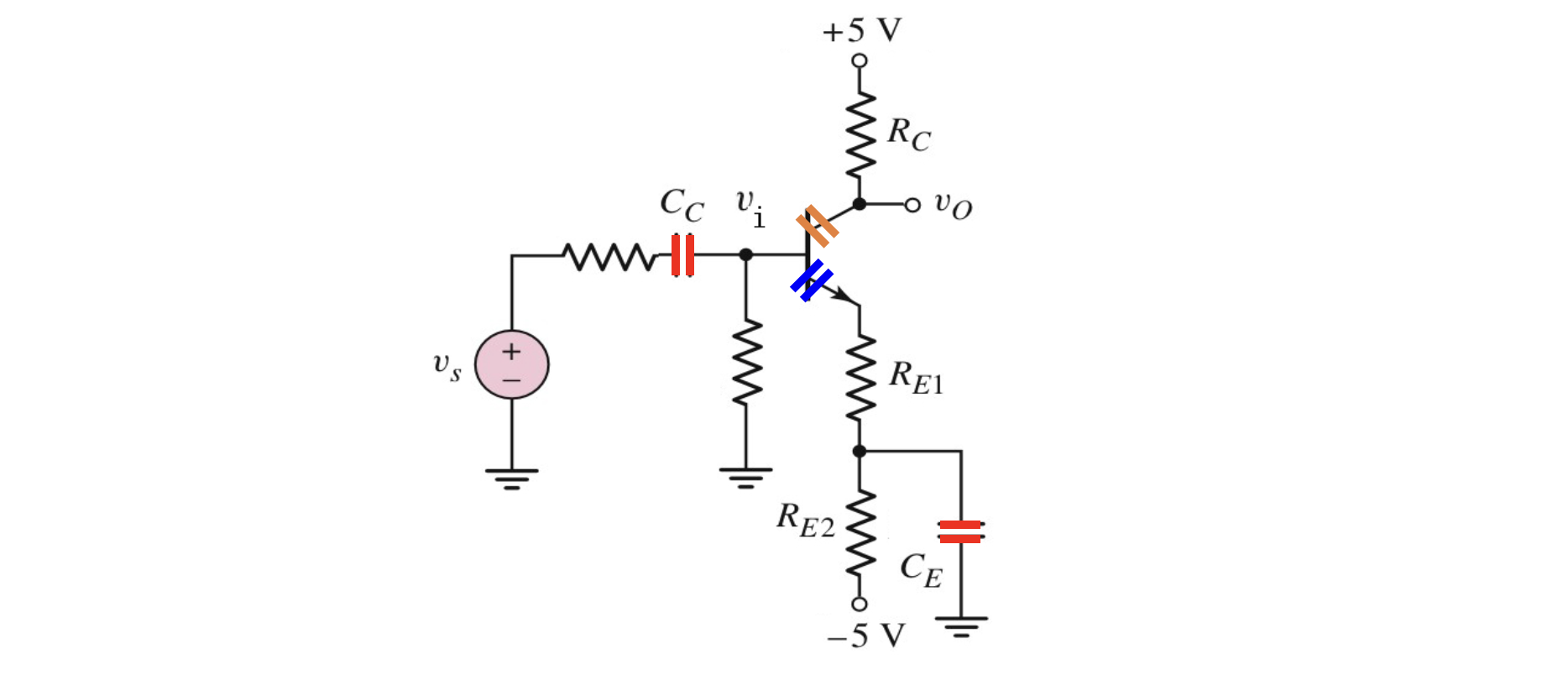
根据容抗公式
- 对于通带,频率不大不小时,按照原来的思路,我们认为
- 对于低频范围
- 对于低频范围
高频的分析难度更大,因为要考虑不再开路的结电容,这部分知识是之前没有涉及的
四、系统传输函数
根据《电路理论》的相关知识,为了更好的研究频率变化对各元件的影响,引入复频率
当频率
电压传输函数(Voltage transfer function)
电流传输函数(Current transfer function)
互阻传输函数(Transresistance function)
互导传输函数(Transconductance function)
显然,这些函数值均为复数。
1. 复频域分析
以下分析的理解涉及到了目前阶段无法详细推导的内容,因此不做要求
根据《信号与系统》方面的知识,传输函数可以表示为
其中
RC 串联电路
先从最简单的 RC 串联电路开始,如下图
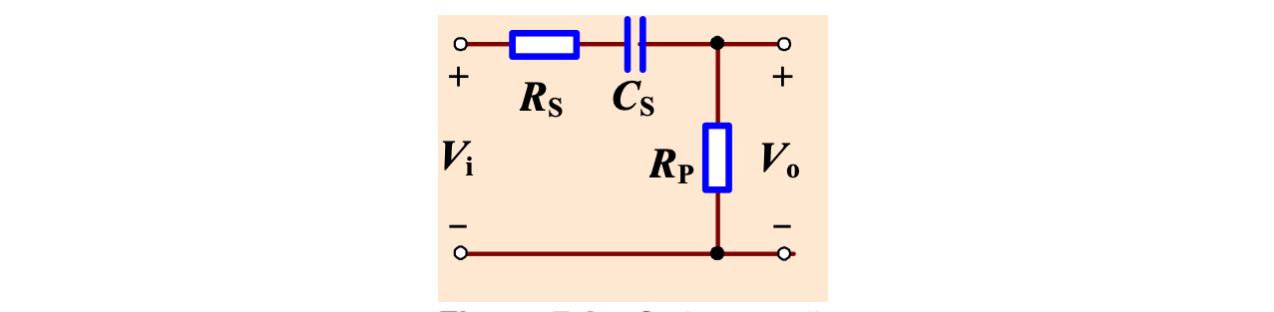
其传输函数可以表示为
令
其中
RC 并联电路
接下来分析 RC 并联电路
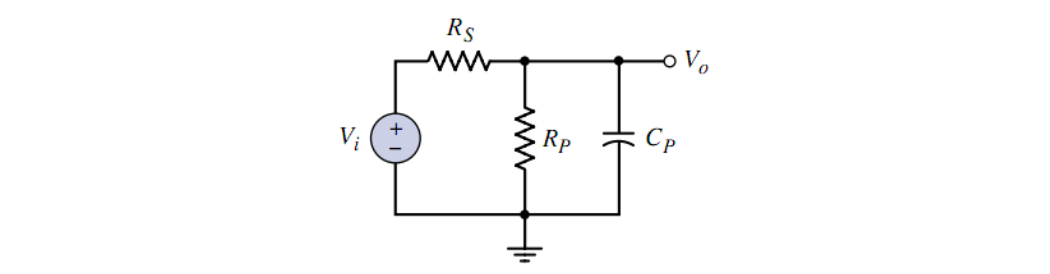
由 KCL 方程有
则经过变换,传输函数为
记
上式化为
综上我们得到了含有单个电容的传输函数表达式
称此函数为「一阶函数」(First-order Funcions)
2. 波得图
将复频率
函数的模为
用分贝表示为
同时,函数的幅角为
现在我们得到了对于一阶 RC 串联电路,随着频率改变,输出信号和输入信号的关系,在幅度变化的同时也产生了移相。
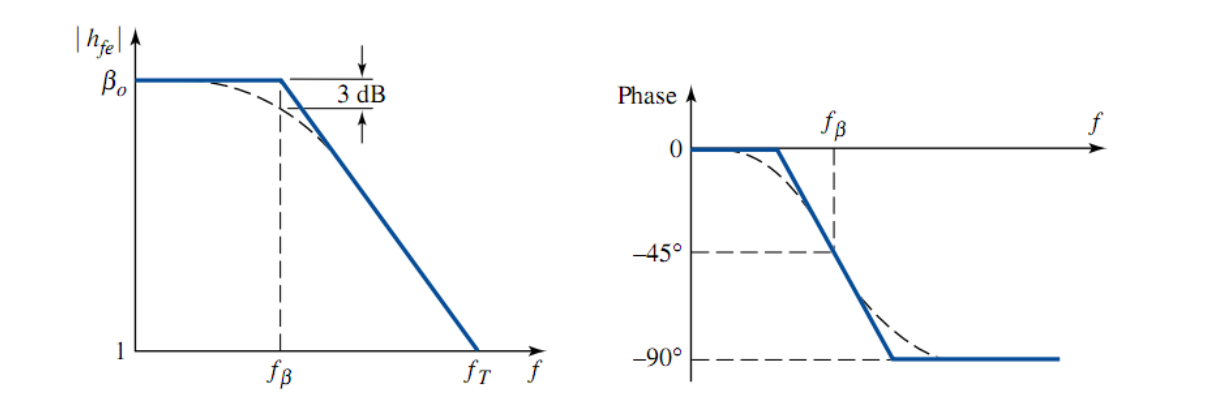
为了直观的表示频率对放大倍数和相位的影响,我们以频率
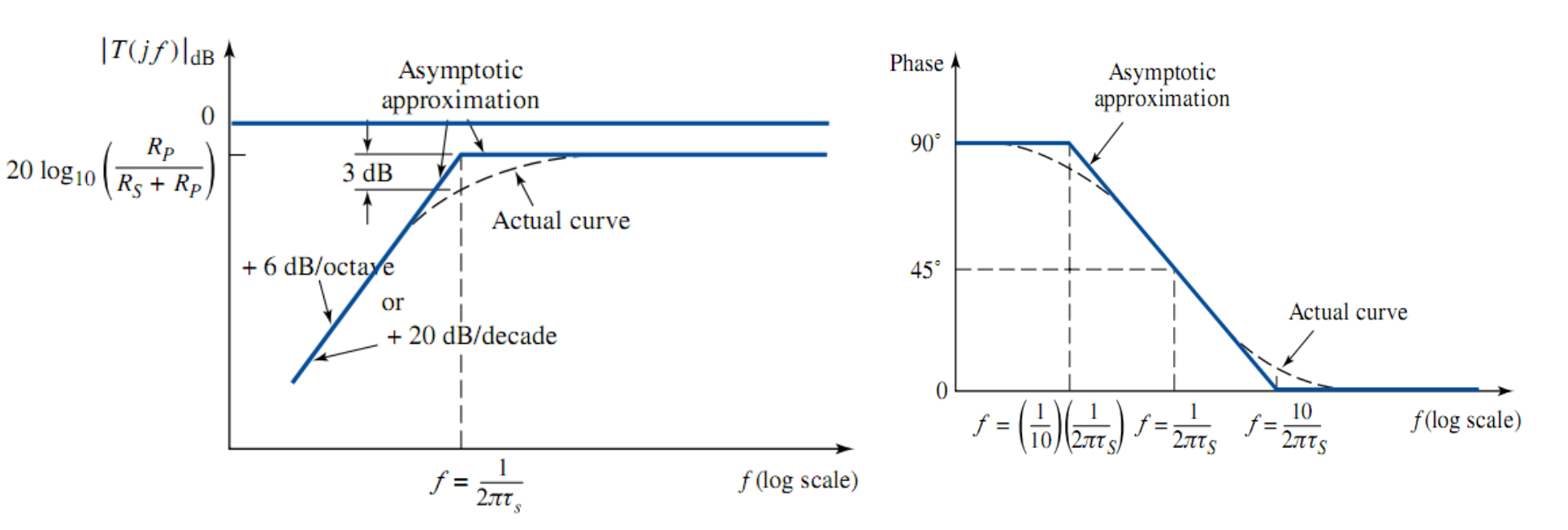
称这种图为「波德图」(Bode plot)。实际上的波德图函数是比较复杂的曲线,因此通常用两条直线来近似,一条为水平直线,其纵坐标为
这种近似产生的误差最大点恰好就在 3dB 点,也叫拐点(corner frequency),
短路和开路的时间常数
回顾
在之前的学习中,要求电路的时间常数,就将所有独立源置零,即电压源短路;电流源开路。然后去求电容两端看进去的等效电阻。
对于串联和并联同时存在的二阶电路
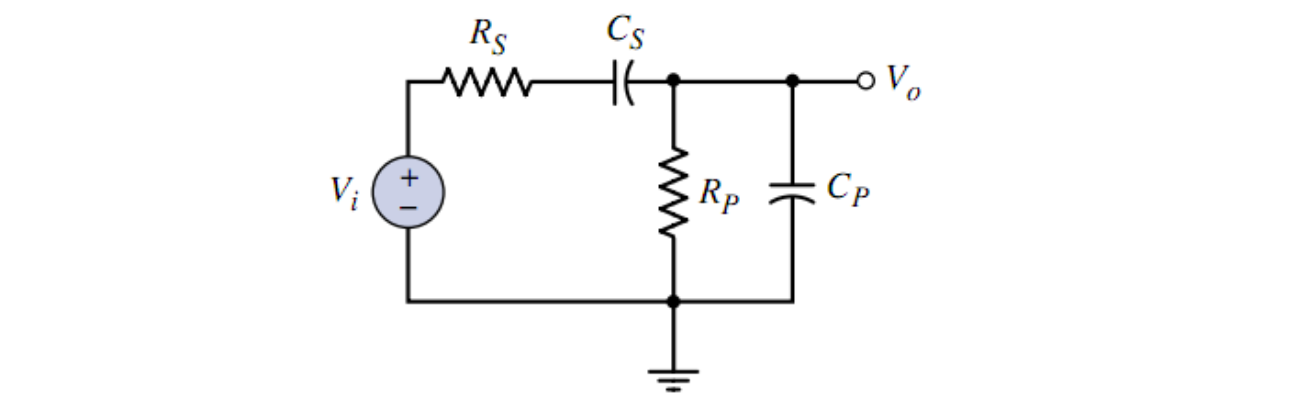
其传输函数为
对于低频工况,
对于高频工况,
因此就得到了幅频响应图的上下限
五、带电容的晶体管放大器
1. 耦合电容效应
耦合电容效应(Coupling Capacitor Effect),用于阻挡直流信号和低频信号
1.1 共发射极电路的输入耦合电容
对于共发射极电路的输入耦合电容,在低频时无法视为短路。那么要如何计算开路时间常数?首先画出小信号模型的等效
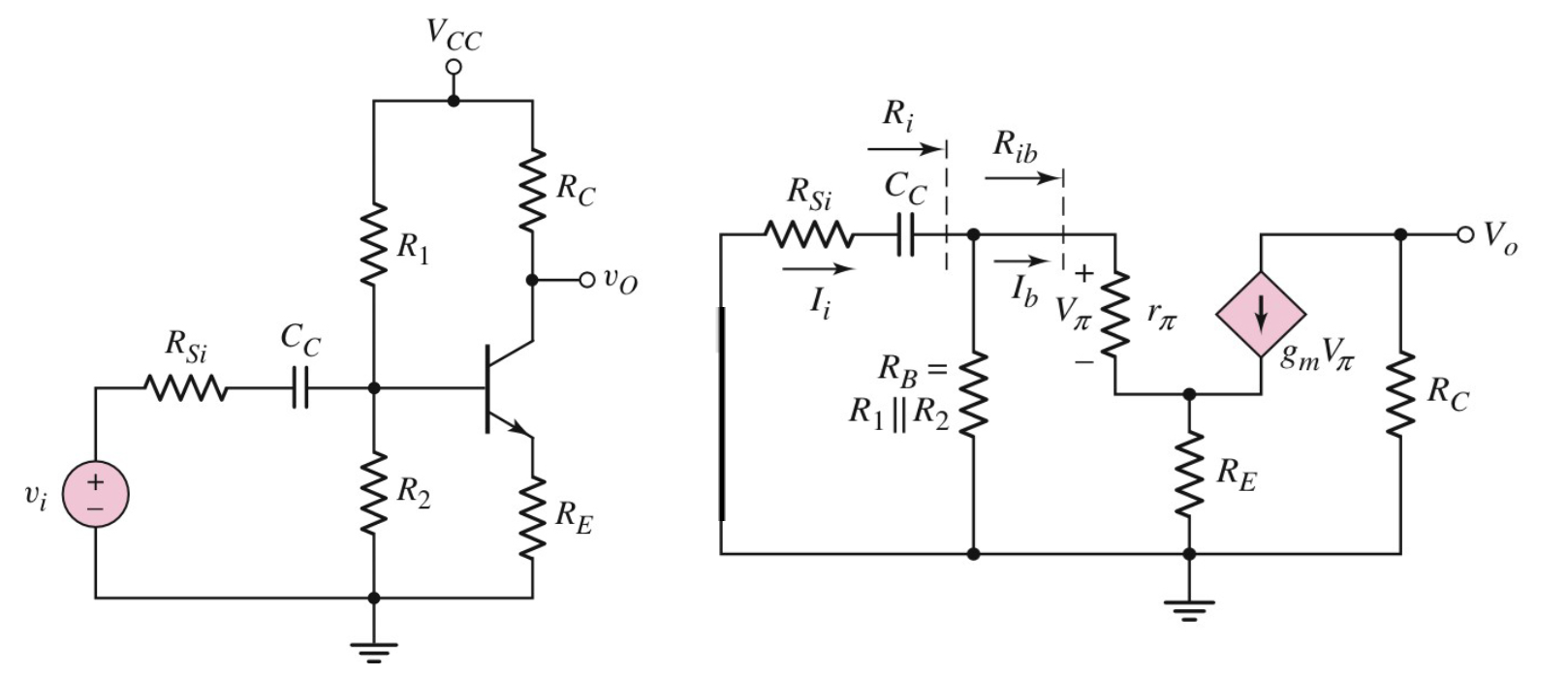
从输入耦合电容
1.2 共发射极电路输出耦合电容
对于输出端的电容,同样可以画出小信号模型的等效
得到时间常数为
1.3 射极跟随器的输出耦合电容
此电路同时具有输入输出电容,如果两个影响的都是低频,考虑其中一个电容的影响时,将另一个视为短路,一个个分析。比如现在我们就将输入耦合电容视为无穷大,单独考虑输出耦合电容的时间常数,画出对应的等效小信号模型
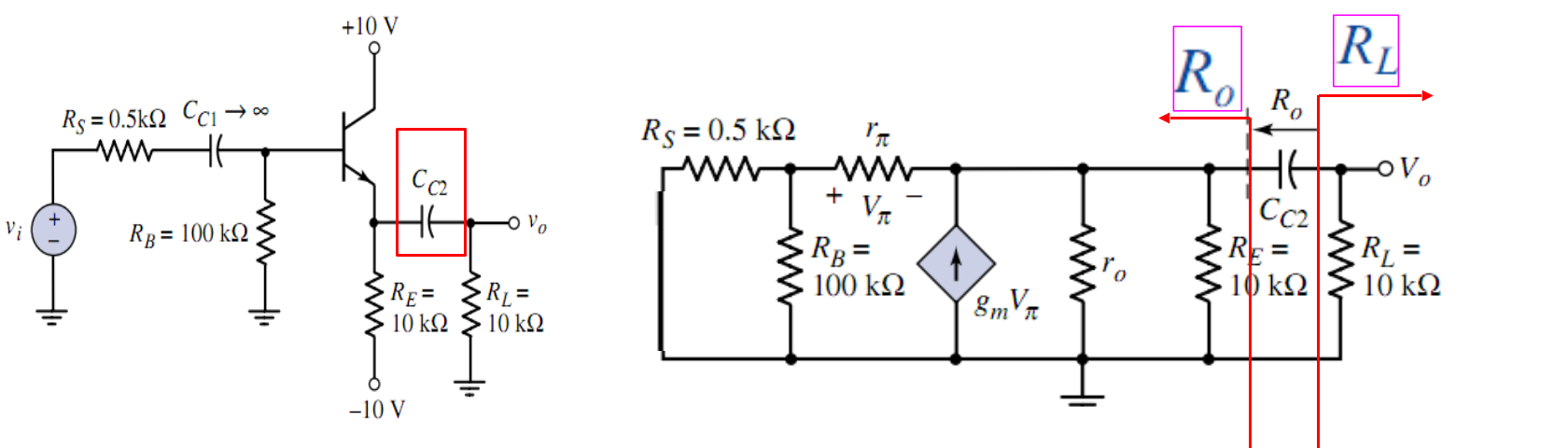
通过电流关系的映射(Mapping)可以得到电容左边的等效电阻为
求出来不同的频率下限,肯定要选更大的,即「考虑最坏情况」
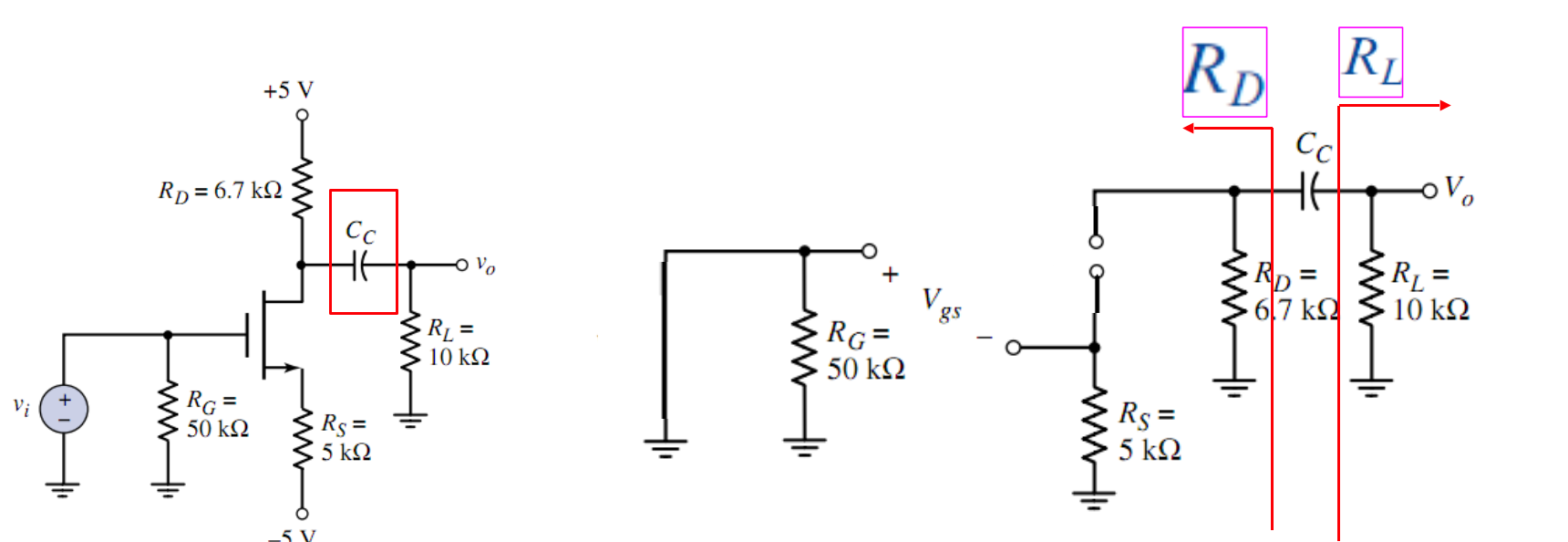
2. 负载电容效应
对于 P 沟道增强型 MOS 管放大器而言,若其负载端有并联电容,此电容一般大小不大,称为「负载电容」,则需要考虑其短路时间常数。首先画出对应小信号模型
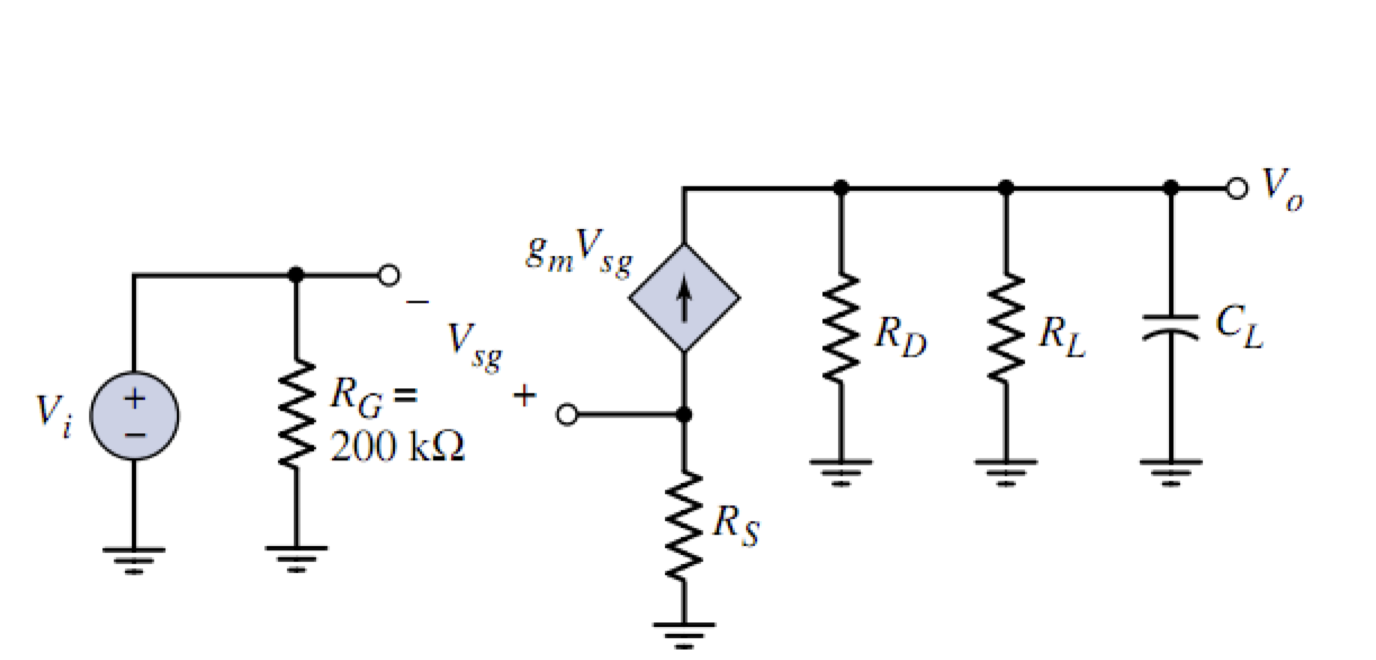
负载电容一般很小,时间常数为
3. 负载电容与输入耦合电容
同时具有这两种电容的时候,由于电容量差很大,分开考虑各算各的,否则将会把问题变为二阶问题。如下图是一个有输入耦合电容和负载电容的共发射极放大电路
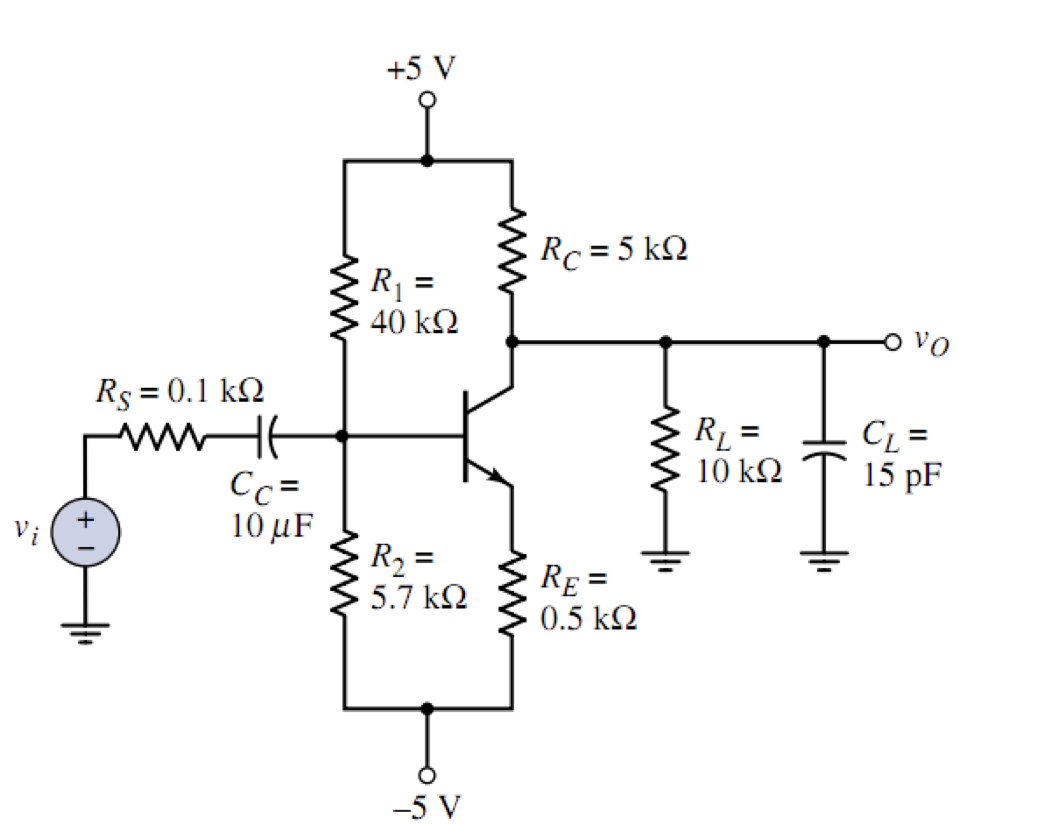
要求两个电容各自的时间常数,则首先画出小信号模型
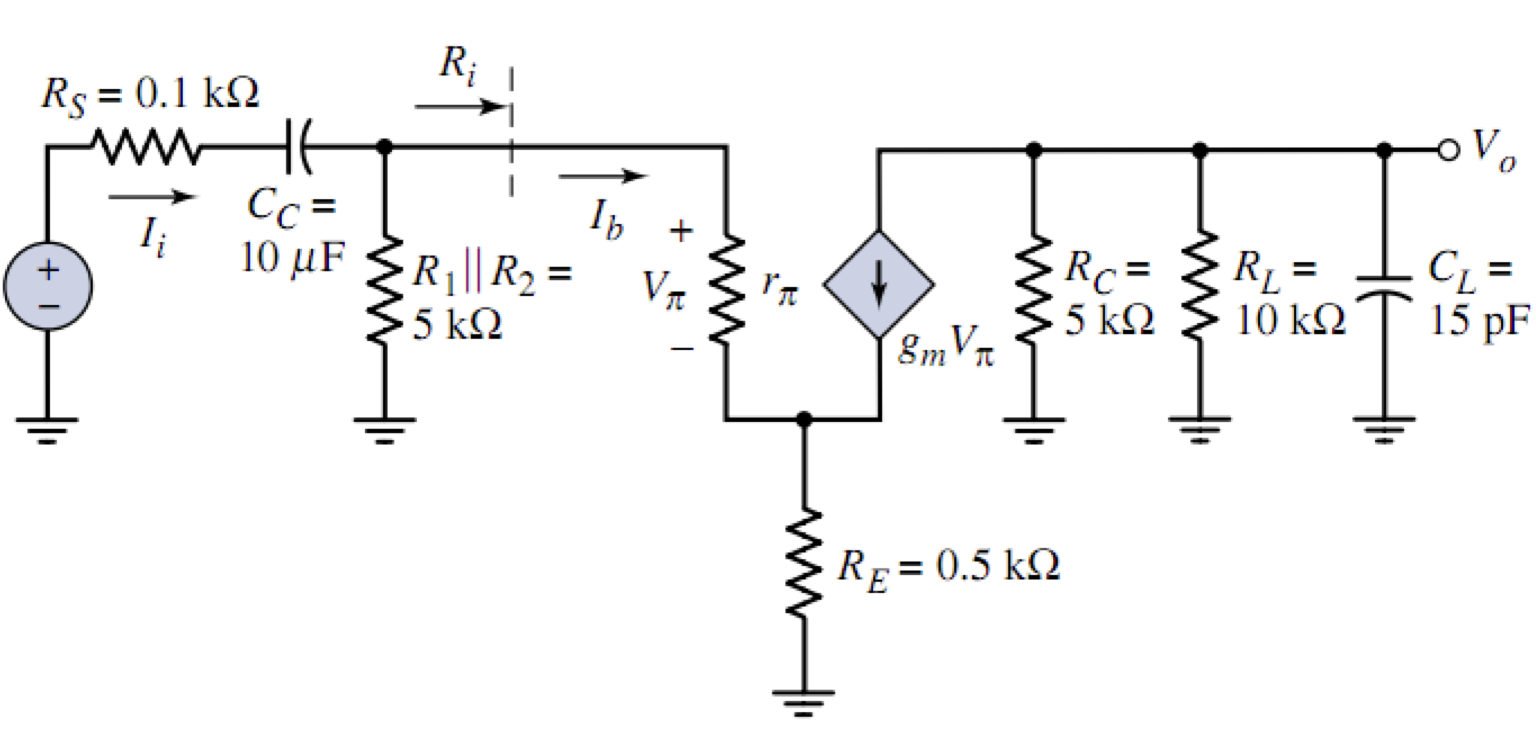
首先将
因此其时间常数可以表示为
4. 旁路电容
在发射极,往往会与发射极电阻并联一个电容,此电容称为「旁路电容」(Bypass Capacitor),用于旁路掉高频电流
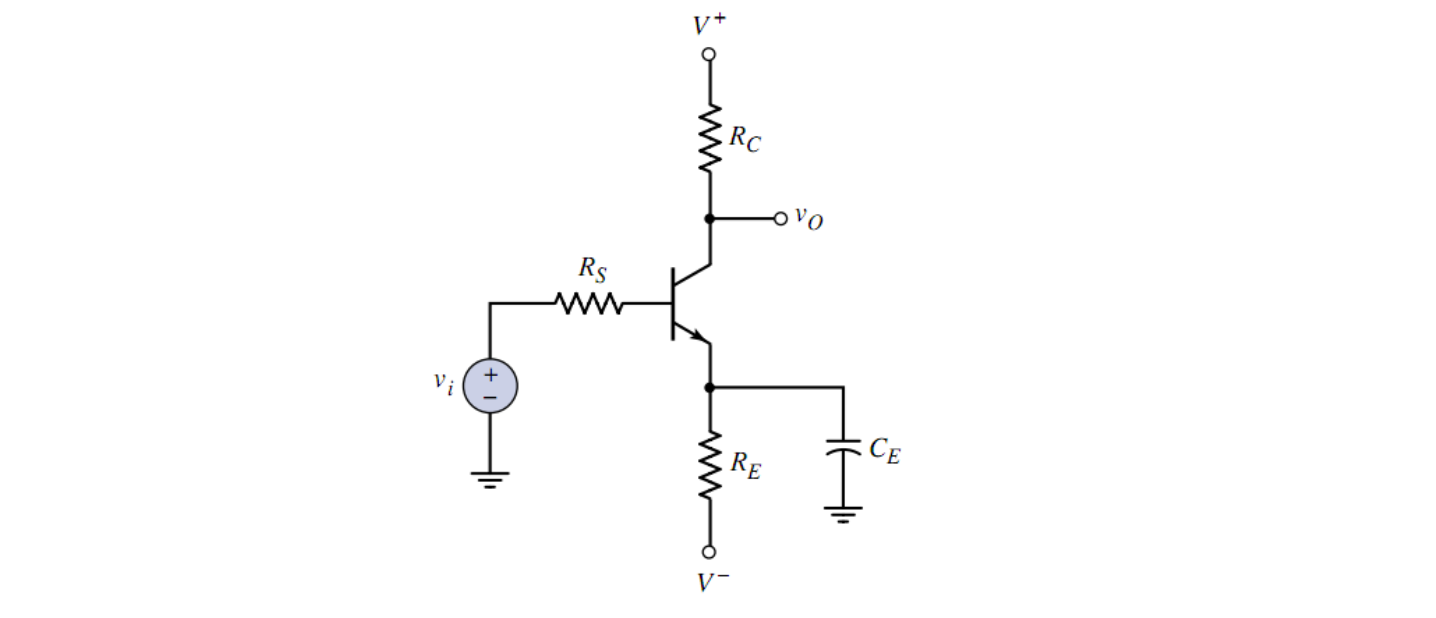
画出小信号模型
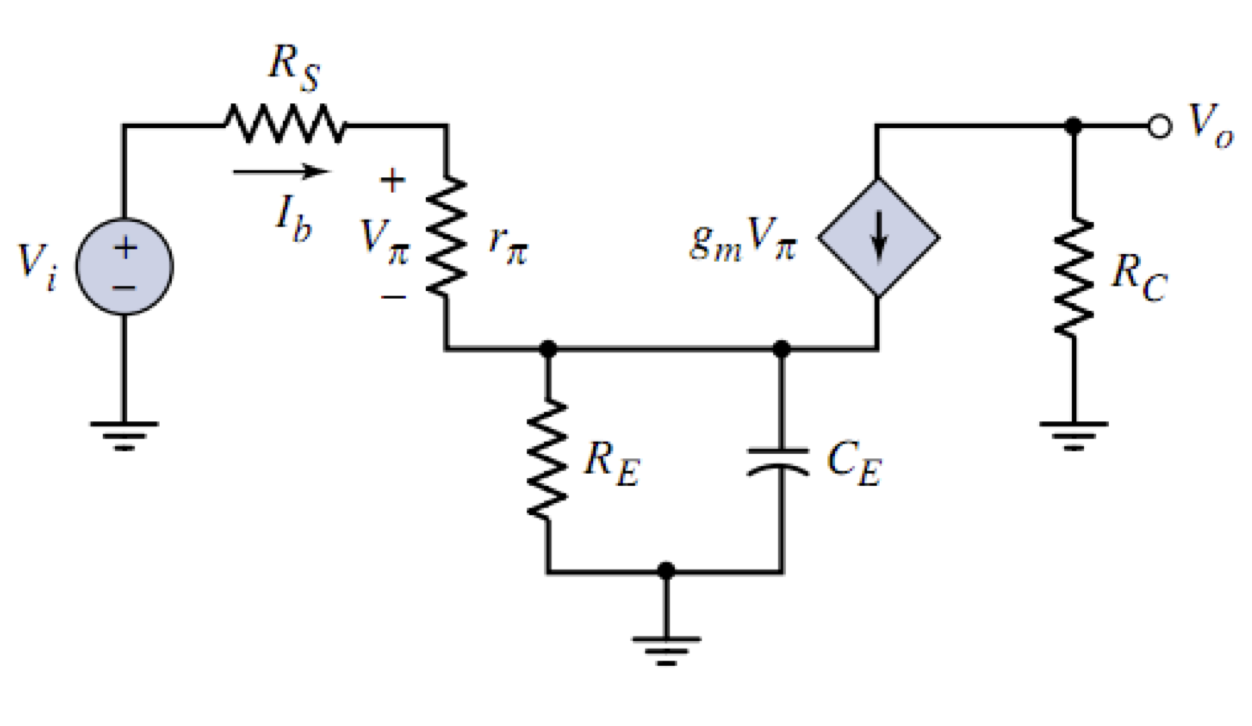
这个电容既在输入回路也在输出回路,意味着可能算出两个
接下来求电压增益。首先,基极电流可以表示为
然后建立输出电压和输出电压的关系
得到
令
则电压增益化为
注意到这里的
因为ce极电流近似相等,因此输出回路的时间常数只需要
而且注意到
因此只需要考虑
Problem-Solving Technique: Bode Plot of Gain Magnitude
Determine whether capacitor is producing a low-pass or high-pass circuit.
Sketch general shape of Bode plot
Corner frequency is f = 1/(2πτ) where τ = ReqC
Req is resistance seen by capacitor
Maximum gain magnitude is midband gain.
Coupling and bypass capacitors act as shorts
Load capacitors act as opens
综合分析
输入耦合电容,输出耦合电容和旁路电容,三个电容谁对频率响应的影响最大?
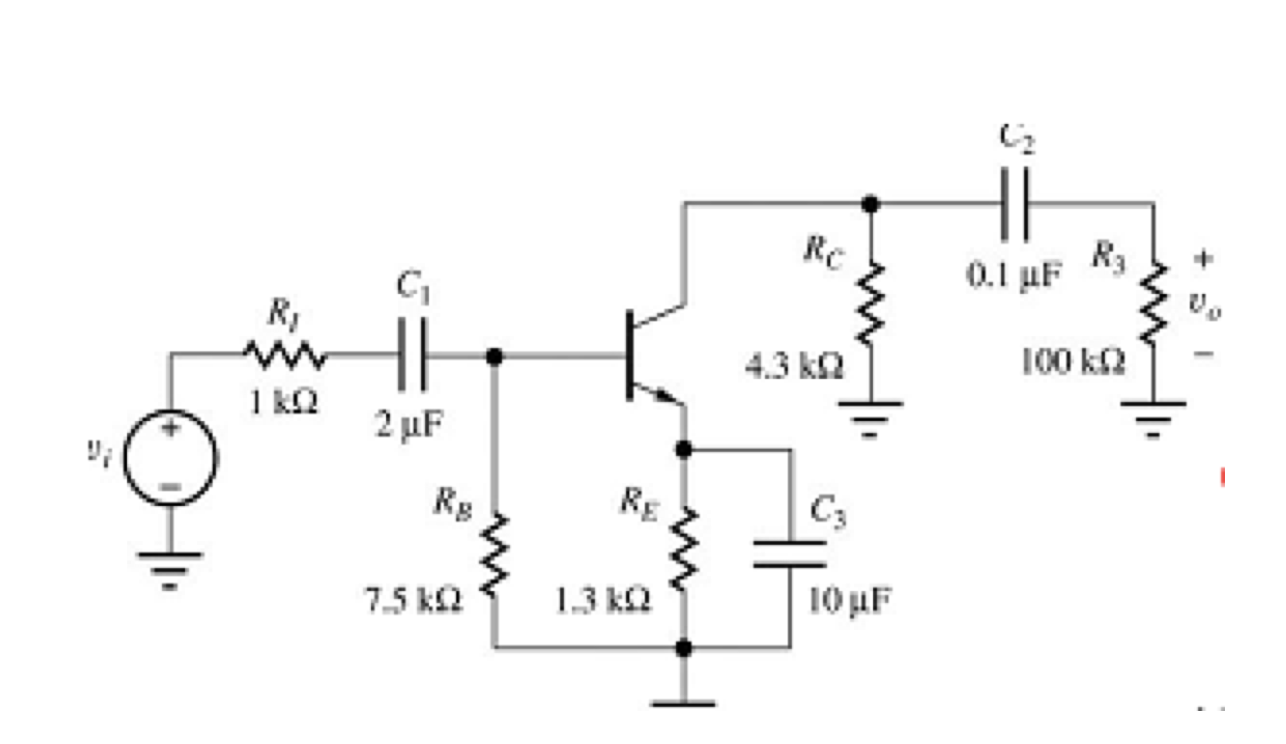
三个电容没法一起算,总不能算个三阶电路吧。分开考虑,算其中一个的时候,把另外两个短路。
考虑交流通路
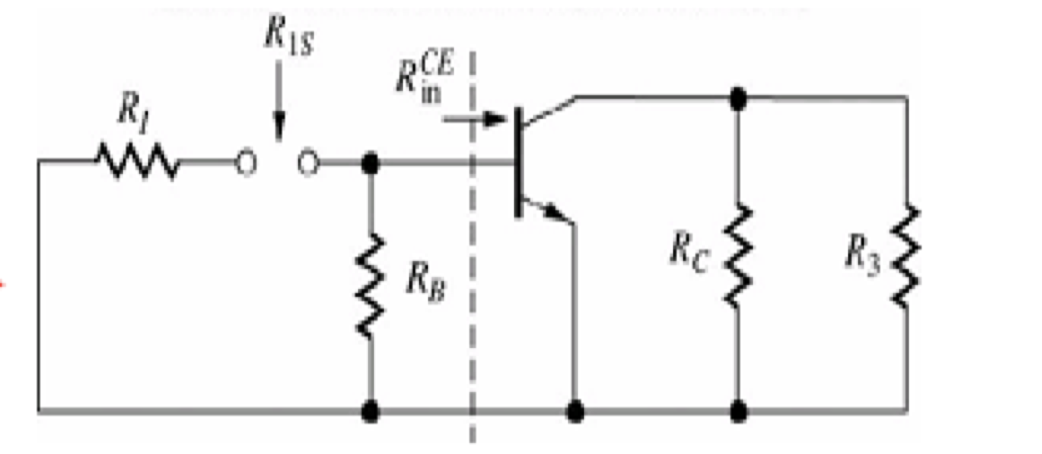
先算
再算
最后算
处理步骤
- 确定电容造成的是高通电路还是低通电路
- 确定
- 找到最大增益
高频段
到高频段,要考虑PN结的结电容,因此不能直接复用小信号模型
六、BJT 的频率响应
1. Hybrid-π 模型的展开
之前提到,BJT 可以用 Hybrid-π 模型来近似,如下图
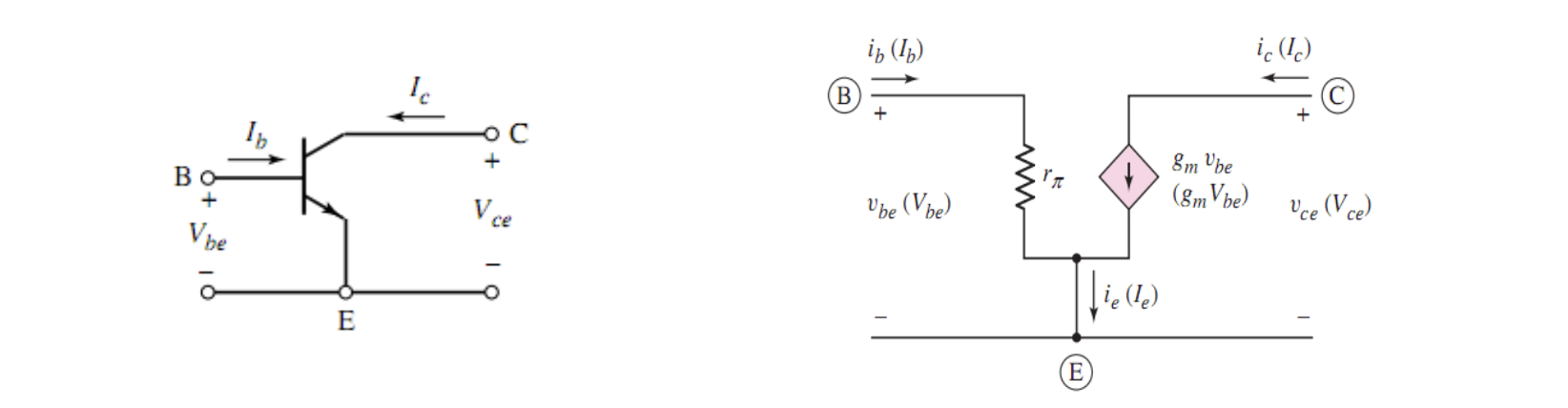
此时我们没有考虑 PN 结中的结电容。但当我们在分析频率响应时,就需要展开 Hybrid-π 模型中被我们忽视的三个结电容
B-E 结电容
B-E 结可以表示为下图
基极可以被分为「外基极」(External base terminal),用 B 来表示,和「内基极」(Internal base terminal),用 B' 来表示。两个基极之间存在一个电阻
同样的,发射极也可以被分成「外发射极」(External emitter terminal),用 E 来表示,和「内发射极」(Internal emitter terminal),用 E' 来表示。两个发射极之间存在一个电阻
在内基极和内发射极之间是一个正偏的 PN 结,可以用一对并联的电阻和电容来替代,分别是「正偏结扩散电阻」(Forward-biased junction diffusion resistance)和「正偏结电容」(Forward-biased junction capacitance)
最后得到的 B-E 结近似可以表示为
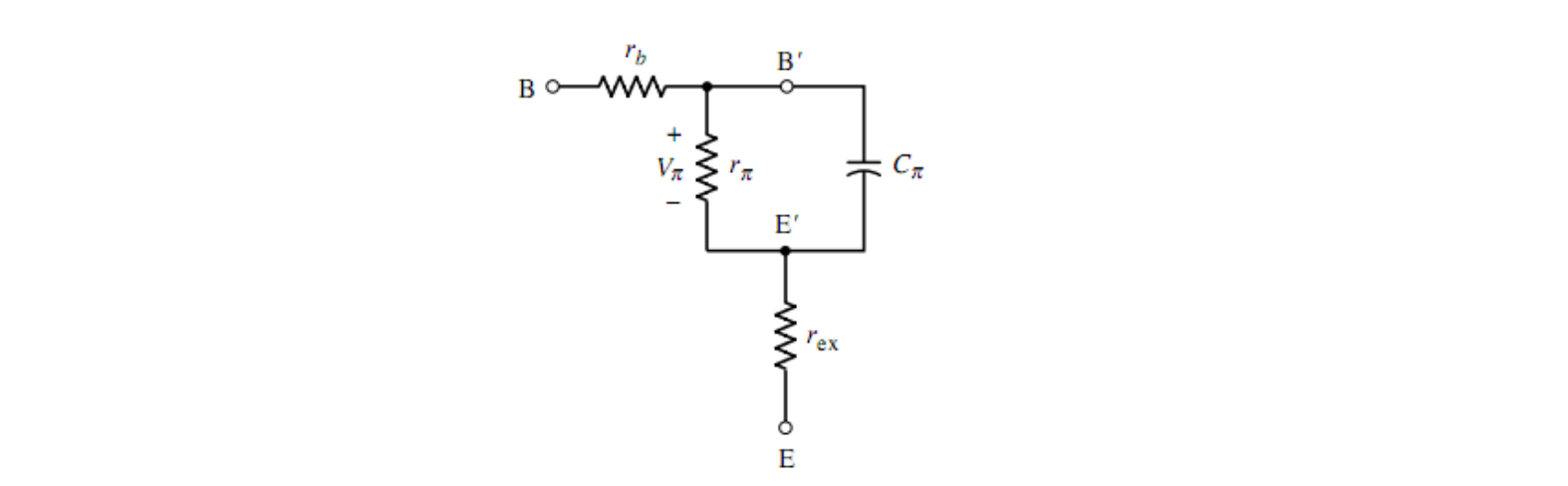
C-E 结
集电极可以被分为「外集电极」(External collector terminal),用 B 来表示,和「内集电极」(Internal collector terminal),用 B' 来表示。两个集电极之间存在一个电阻
在内集电极和内发射极之间,等效为一个非理想电流源,即一个理想电流源与电阻的并联。电流源内阻
最后得到的 C-E 结近似可以表示为
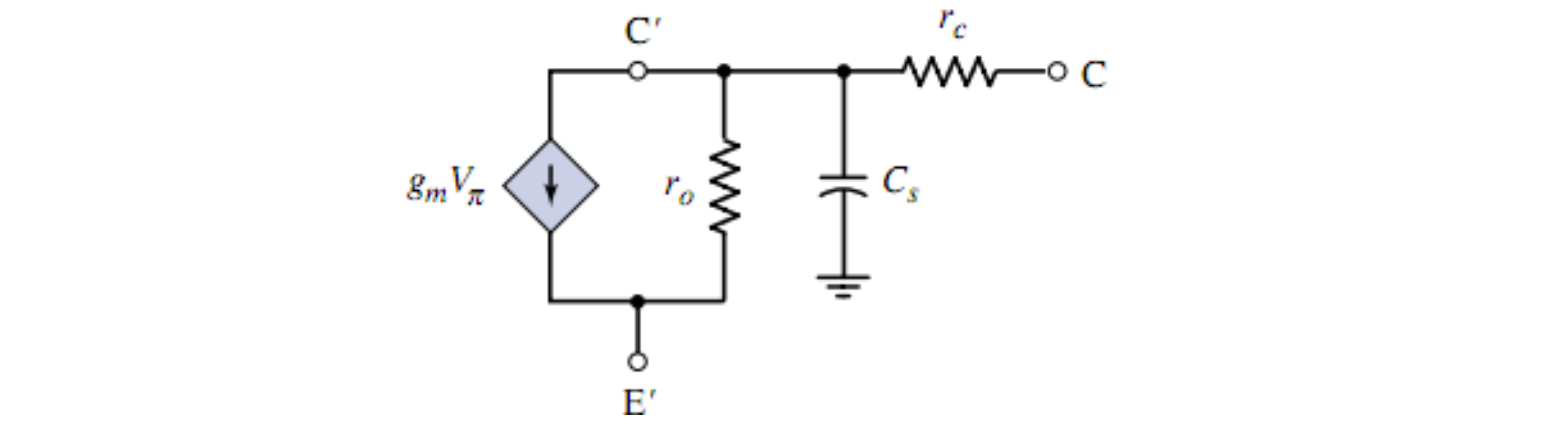
B-C 结
因为要考虑电容电流,所以不能用
在内集电极和内基极之间同样可以用一对并联的电容和电阻替代,电阻被称为「反偏扩散电阻」(Reverse- biased diffusion resistance),通常在
由于反偏扩散电阻非常大,因此反偏节点容通常可以忽略
考虑电容效应的 Hybrid-π 模型
接下来进行进一步简化,把大电阻开路,小电阻短路最后得到的等效电路如图
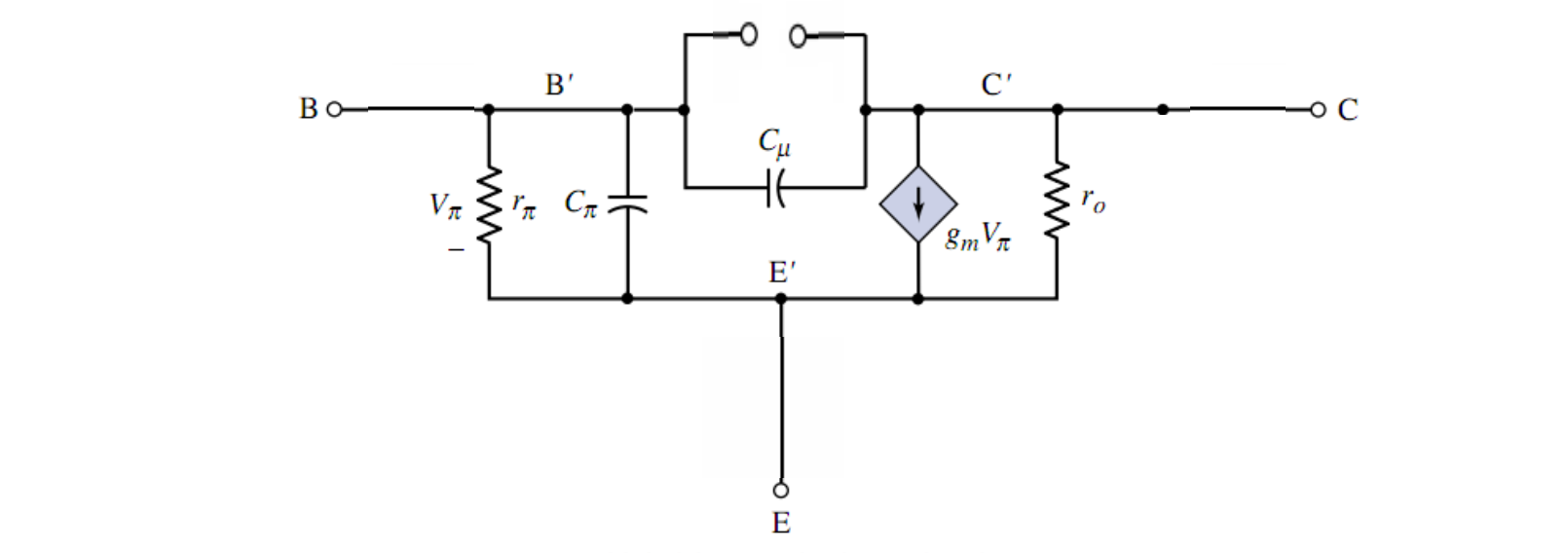
对于高频情况下,传统我们认为的
连接高频模型中的 CE 端,考察短路情况下,
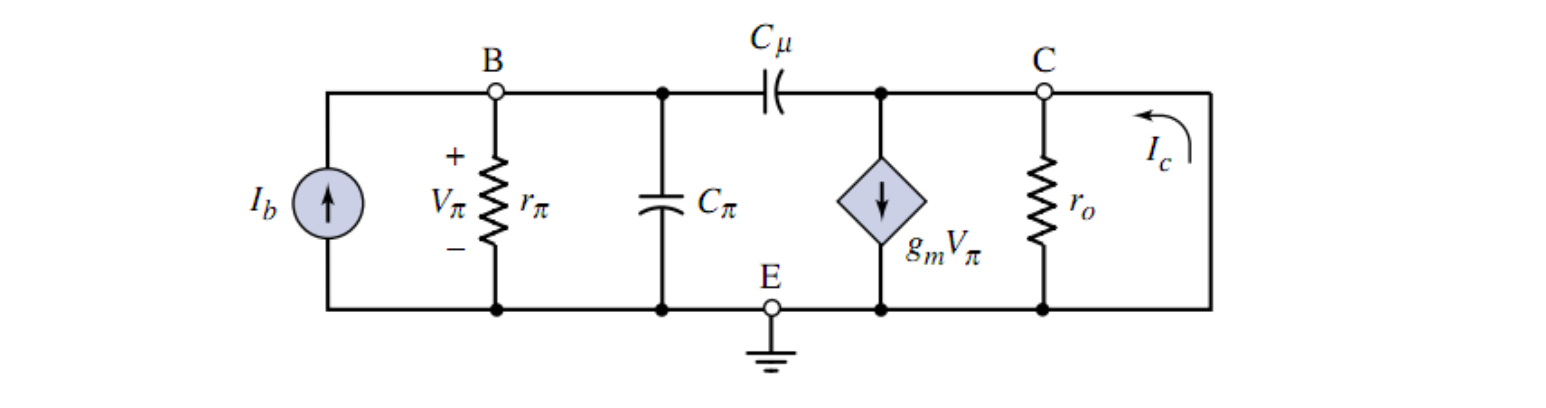
根据 KCL
根据 KVL
可以化为
由于
其实可以等效为一个低通网络,如下图
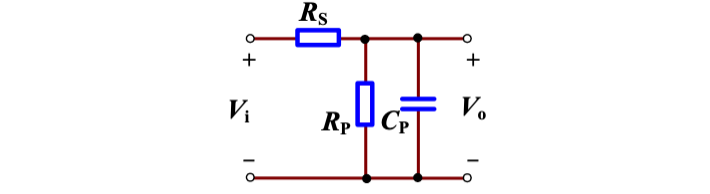
其截止频率为
波德图可以表示为
2. 密勒效应
大电容照常短路,求小电容的影响
画出小信号模型和三极管模型
电容把输入和输出连在了一起,造成了反馈。如何进行分割?
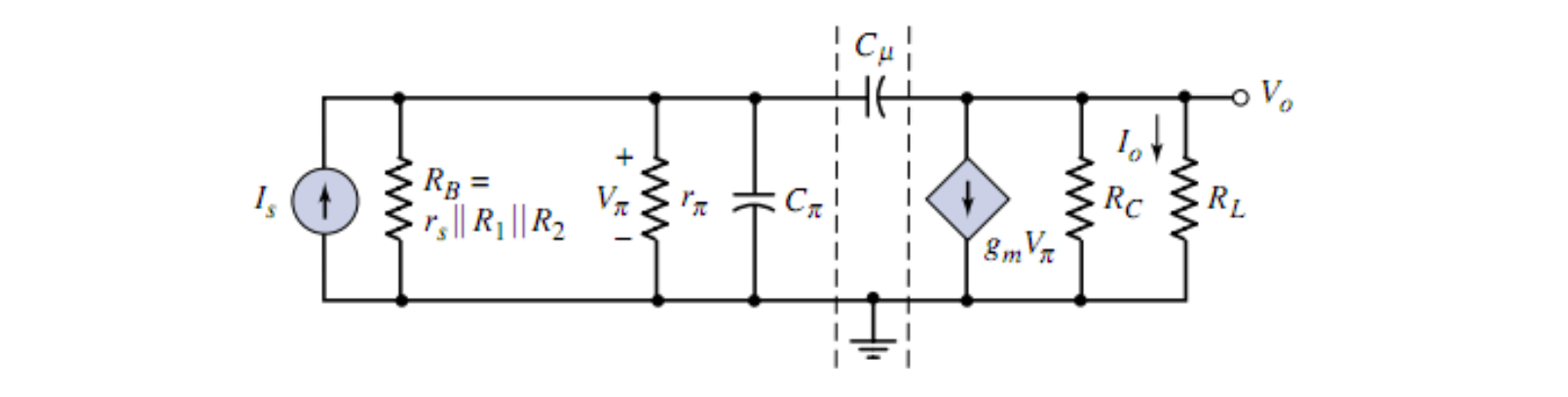
电容对输出没有影响,因此「可以折」。通过电容
得到
由于
进一步可以得到
其中
通过密勒折合,把一个小电容折合成了一个很大的电容,导致带宽变窄,称为「密勒效应」(Miller Effect)。折合后的米勒电容如下图
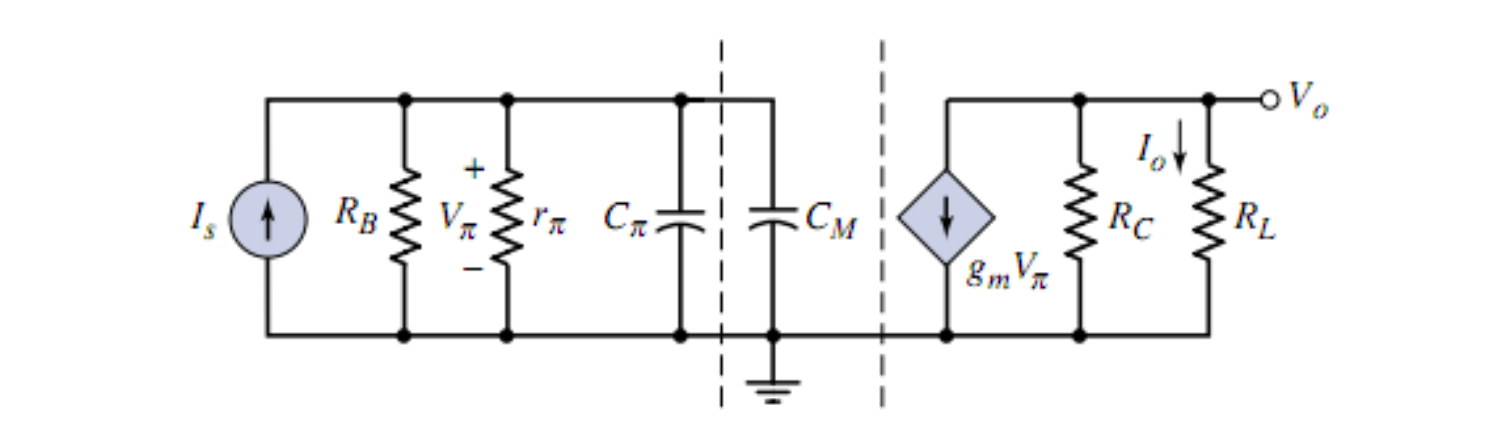
由此,通过密勒效应,将电容「折」到输入端,输出端做一个整理
其中
得到频率上限
发现增益和频率上限的乘积,或者说增益和带宽的乘积是一个常数。密勒效应的结论告诉我们,任何共源极或共发射极放大电路注定不会有很宽的带宽,而共基极或共栅极放大电路带宽很宽,显然,电压跟随器带宽最宽。
3. 结论
BJT 放大电路中,过高和过低的频率都不能很好地通过,对于低频段,耦合电容和旁路导致增益下降,而对于高频段,BJT 内部的结电容导致增益下降,只有在在中间频段,不考虑任何电容。将耦合电容和旁路电容视为短路,将结电容视为开路
对于多级,前级的输出是后级的输入,因此有
多级放大电路的增益比任何一个单极放大电路都要大,带宽都要窄
增益和带宽的积维持不变
考试要求
不考计算,只要求定性,唯一需要一些的就是滤波器部分