一、逻辑代数基本定理与恒等式

1. 逻辑代数和逻辑关系

1.1 逻辑代数

逻辑代数，又称布尔代数，是分析和设计现代数字逻辑电路的数学工具。逻辑代数的定律、定理和规则，用于对表达式进行处理，以完成对逻辑电路的化简、变换、分析和设计

1.2 逻辑关系

逻辑关系是事件产生的条件和结果之间的因果关系。在数字电路中，将事情的条件作为输入信号，结果作为输出信号。条件和结果中两种对立状态分别用逻辑 1 和 0 表示

2. 基本定律和恒等式

2.1 基本定律

0-1 律

$，$

重叠律

互补律

结合律

交换律

分配律

注意，或运算分配律与普通代数运算不同！

摩根律

吸收律

2.2 恒等式

证明：

$左式$

2.3 等式证明的方法

代数法

通过逻辑代数运算得到等式相等

穷举法

将等式两边分别用，表示，穷举输入变量所有取值的组合，分别代入和算出相应的结果。若都相等，则，否则

3. 逻辑代数的基本规则

3.1 代入规则

定义

任何含有某变量的等式，若等式中所有出现改变量的位置均代之以一个逻辑函数式，则此等式依然成立。

应用

由此规则，可以扩大基本共识的应用范围，比如摩根律可以拓展到 n 个变量

3.2 反演规则

定义

对于任意一个逻辑函数式，做如下处理，得到的新函数式称为原函数的反函数式

与运算换成或运算，或运算换成与运算
常量 0 换成 1，1 换成 0
原变量换成反变量，反变量换成原变量
保持原函数的运算次序不变

注意

为了保持原函数运算次序不变，必要时可以加入括号
对于不属于单个变量上的非号，可以将非号去掉，而其下的函数式保持不变

例如

则其反函数可以表示为

3.3 对偶规则

定义

任意逻辑函数式，作如下处理，得到的新函数式称为原函数式的对偶式

与运算换成或运算，或运算换成与运算
常量 0 换成 1，1 换成 0
保持原函数的运算次序不变

注意

为了保持原函数运算次序不变，必要时可以加入括号

定理

若，则

4. 逻辑函数的形式

任何逻辑函数都存在五种等价的形式

1. 与-或式

定义最简与或表达式：与项数最少，且各与项中变量数最少的与或表达式

2. 与非-与非式

由摩根律

3. 或-与式

4. 或非-或非式

5. 与或非式

任何表达式都可变换为上述五种形式的表达式

最简与或表达式:与项数最少，且各与项中变量数最少的与 - 或表达式

二、逻辑函数表达式的形式

1. 最小项表达式

1.1 最小项的定义

个变量的最小项是个因子的乘积，各变量都必须以其原或反变量的形式在乘积项中出现且仅出现一次

个变量的最小项应该有个。如对于三变量而言，有最小项：

$，，，，，，，，$

1.2 最小项的性质

任意一个最小项，只有一组变量取值使得它的值为 1
不同的最小项，使得它的值为 1 的那一组变量取值也不同
全部最小项之和为 1

1.3 最小项的编号

用 1 表示最小项中的原变量，用 0 表示反变量，由此得到一个二进制数。用来表示最小项。则与此二进制数对应的十进制数即下标的值

1.4 最小项表达式

由若干最小项构成的与或表达式称为「最小项表达式」。

任何逻辑函数都可变换成唯一的最小项表达式。

代数转换法

将逻辑函数转换成一般与或式，再反复使用，将所有非最小项的与项变成最小项。

如对于

再拓展成最小项

真值表转换法

最小项表达式是若干最小项构成的，若某组变量值使表达式，则中一定有该组变量值所对应的结果为的最小项。因此只需要将逻辑函数转换成一般与或表达式，再列真值表，写出标准与或表达式。

2. 最大项表达式

2.1 最大项的定义

个变量的最大项是个因子的或项，各变量都必须以其原或反变量的形式在或项中出现且仅出现一次

个变量的最小项应该有个。如对于三变量而言，有最大项：

$、、、$

2.2 最大项的性质

任意一个最大项，只有一组变量取值使得它的值为 0
不同的最大项，使得它的值为 0 的那一组变量取值也不同
全部最大项之积为 0

2.3 最大项的编号

用 1 表示最大项中的原变量，用 0 表示反变量，由此得到一个二进制数。用来表示最大项。则与此二进制数对应的十进制数即下标的值‘

2.4 最大项表达式

由若干最大项构成的乘积表达式称为「最大项表达式」。

任何逻辑函数都可变换成唯一的最大项表达式。

2.5 最小项和最大项的互补关系

三、逻辑函数的代数化简法

代数法化简可以降低电路成本，以较少的门实现电路，或减少使用的门电路的种类

四、逻辑函数的卡诺图化简法

1. 用卡诺图表示逻辑函数

1.1 卡诺图

如果两个最小项只有一个变量互为反变量，那么称这两个最小项「在逻辑上相邻」。

将变量的全部最小项用方格表示，并使具有逻辑相邻的最小项在几何位置上也相邻地排列起来，这样得到的图形叫做变量的「卡诺图」

个变量有个最小项，个变量的卡诺图由个方格组成，每一个方格代表坐标值对应了一个最小项。

1.2 卡诺图的特点

相邻方格对应的最小项只有一个因子的差别，故其坐标按循环码排列，如

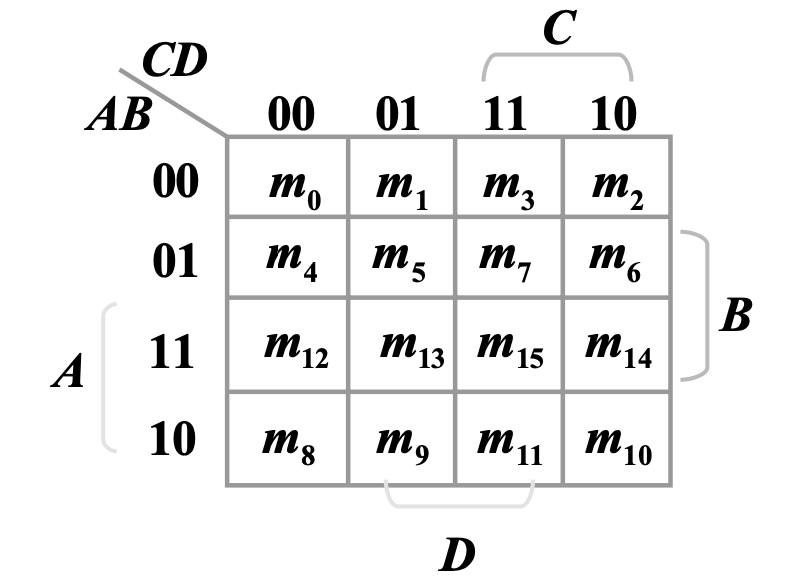
在卡诺图上，相邻方格的最小项，在逻辑上也是相邻的。卡诺图的几何相邻包括：

相接——即紧挨着的
相对——任一行或一列的两头
相重——对折起来后位置相重

个变量的最小项，有个相邻的最小项可合并

1.3 逻辑函数的卡诺图

当逻辑函数为最小项表达式时，将表达式中出现的最小项对应的方格，在卡诺图中标为 1 ，其余方格标 0 (也可不标)，便得到逻辑函数的卡诺图。

由最小项表达式的性质，任何逻辑函数都等于其卡诺图中标 1 方格所对应的最小项之和

卡诺图本质上是真值表的一种平面几何图形表示方法

若一组变量值使逻辑函数为 1 ，则该组值便是其卡诺图中标 1 方格的坐标

画卡诺图的步骤

求逻辑函数的与或式
根据变量数确定卡诺图形式
根据各与项，在卡诺图上标 1

2. 卡诺图化简逻辑函数

2.1 卡诺图化简的依据

卡诺图中相邻方格对应的最小项在逻辑上相邻，而逻辑相邻的最小项可合并。因此可以在卡诺图上画圈来合并最小项

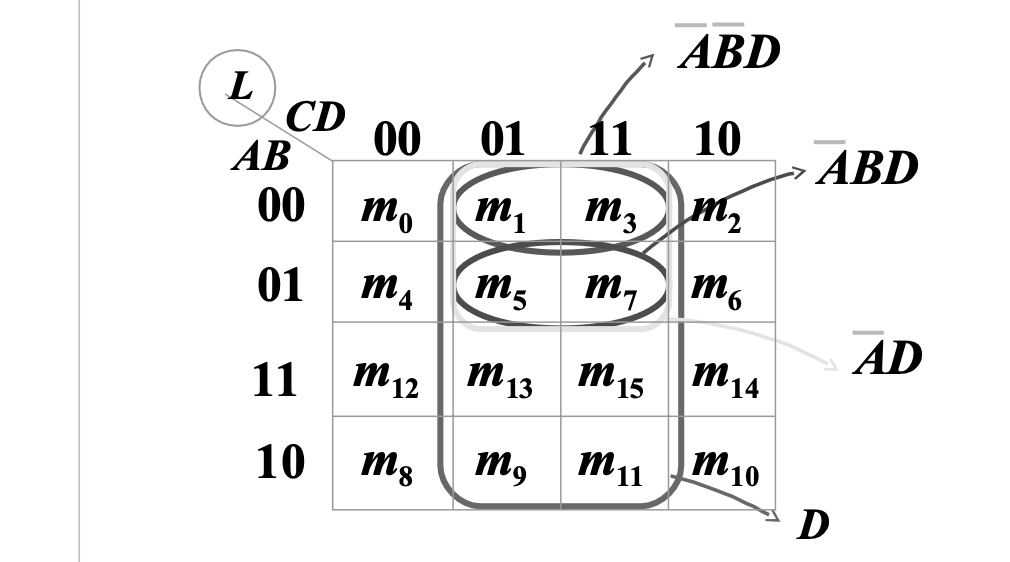
如上图

任何逻辑函数都等于其卡诺图中为 1 的方格所对应的最小项之和，因此若将卡诺图中 1 方格所对应的最小项合并，则达到化简的目的

2.2 卡诺图化简的步骤

将逻辑函数转换为与或表达式
根据逻辑函数与与或表达式填卡诺图，得到逻辑函数的卡诺图
合并最小项
- 相邻的个 1 格圈为一个卡诺圈，各圈对应一个乘积项
- 1 格可重复被圈，但新增圈中必须有未曾被圈过的 1 格
- 卡诺圈中的格数尽量多，卡诺圈的数量尽量少
将各卡诺圈对应的乘积项相或，得到最简与或表达式

3. 卡诺图设计电路

可以先列出真值表，再画出对应卡诺图，从而得到一个最简与或式。

五、Verilog HDL

1. Verilog HDL 基础

硬件描述语言（Hardware Description Language）

类似于高级程序语言，文本形式描述数字电路结构和行为的语言
可描述逻辑电路图，逻辑表达式，信号及逻辑电路功能行为

逻辑仿真

用计算机仿真软件对数字逻辑电路的结构和行为进行预测
仿真器对 HDL 描述进行解释，以文本或波形描述电路输出

逻辑综合

根据 HDL 描述导出电路基本元件表及其连接关系(门级网表)的过程
类似高级程序语言的编译过程
根据网表数据库，可制作出集成电路或印刷电路板 PCB

时序仿真（后仿真）

2. Verilog 的基本语法规则

2.1 基本符号

间隔符

用于分隔文本，如：空格符（\b）、TAB 键（\t）、页符

注释符

用于改善可读性，不影响编译。

多行注释符：/---/
单行注释符：以 // 开始到行尾结束为注释文字

标识符

用字符串表示对象（如模块、输入/输出端口、变量），以英文字母或下划线开始，如 clk , counter8 , _net , bus_A

关键词

用来定义语言结构的特殊词汇。关键词都是小写，关键词不能作为标识符使用，如 module , endmodule , input , output , wire , reg , and 等

逻辑值集合

Verilog 语言规定了四种基本的逻辑值

0：表示逻辑 0，逻辑假
0：表示逻辑 1，逻辑真
x 或 X：不确定的值（未知状态）
z 或 Z：高阻态

常量

可分为整数型常量和实数型常量

整数型常量

可采用十进制数的表示的方法，来表示有符号常量。例如：30，-2

也可采用带基数的形式的表示方法表示常量，格式为

$位宽基数符号数值$

例如： $，，$

实数型常量

十进制计数法，如： $，，$
科学计数法，如： $，$

其中下划线没有实际含义

符号常量

Verilog 参数定义语句可定义标识符表示常量，称为符号常量，格式为

parameter 参数名 1 = 常量表达式 1, 参数名 2 = 常量表达式 2,

字符串是双撇号内的字符序列

3. 变量的数据类型

3.1 线网型变量

用于表示连线，一般指电路中的物理连接。例如，线网型变量的值的值由与门的驱动信号和所决定。 $，$ 的值发生变化，线网的值会立刻跟着变化

常用的线网类型由关键词 wire 定义，格式如下

wire [n-1:0] 变量名 1, 变量名 2,

其中表示线网型变量的位宽度为

3.2 寄存型变量

用于行为描述时，暂存临时状态或中间结果。

寄存型变量只能在 initial 或 always 语句块内被赋值。行为级描述是电路功能行为的抽象描述，并不描述电路的具体结构。

寄存器类型的变量可以分为四种

reg：1 位寄存型变量
integer：32 位带符号的整数寄存型变量
real：64 位带符号的实数型寄存器变量
time：64 位无符号的时间寄存器类型

例如

reg clock // 定义一个 1 位的寄存型变量
rege[3:0] counter; // 定义一个 4 位寄存器类型变量

4. 运算符及其优先级

4.1 运算符

位拼接运算符

将两个或多个信号的某些位拼接起来成为一个新的操作数

设 $A = 1'b1 , B = 2'b10 , C = 2'b00 $

位运算与缩位运算

$：$ 与进行位运算，得到

而缩位运算是各个位之间做缩位运算

符号	意义
{} {{}}	拼接，复制
unary+, unary-	单目正负
+ - * / **	算术
%	模
> >= < <=	关系
!	逻辑非
&&	逻辑与
\|\|	逻辑或
==	逻辑相等
!=	逻辑不等
===	全等
!==	不全等
~	位非
&	位与
\|	位或
^	位异或
^～or～^	位同或
&	单目位缩与
-&	单目位缩与非
\|	单目位缩或
~\|	单目位缩或非
^	单目缩位异或
～^or^~	单目缩位同或
<<	逻辑左移
>>	逻辑右移
<<<	算术左移
>>>	算术右移
?:	条件

5. 基本门级元件

门级建模：将逻辑电路图用 HDL 规定的文本语言表示出来

使用语法

and A1(out,in1,in2,...); // 多输入门
not N1(out1, out2, ..., in) // 多输出门
bufif1 B1(ctrl,in, out); // 三态门

5.1 多输入门

只允许有一个输出，但可以有多个输入.

语句	门
and	与门
or	或门
xor	异或门
nand	与非门
nor	或非门
xnor	异或非门

5.2 多输出门

语句	门
buf	缓冲器
not	反相器

5.3 三态门

语句	门
bufif1	高电平有效控制三态缓冲器
bufif0	低电平有效控制三态缓冲器
notif1	高电平有效控制三态反相器
notif0	高电平有效控制三态反相器

6. Verilog 程序的基本结构

module ABC(port1 ， port2, ...); // 各模块通过端口相互连接
  inout/input/output ... ; // 端口类型说明
  reg/wire/ ... ; // 变量类型说明
  parameter ... ;// 参数定义，逗号分割多个参数
  and/or/ ... ; // 结构描述方式 , 逻辑门或底层模块
  assign...;  //数据流描述方式, 连续赋值语句
  always/initial  //行为描述方式, 过程块结构
  begin // 多条语句组成的行为描述块
    if ... else ... ;// 条件描述语句
    case // 分支描述语句
      ... 
    endcase // 无实际语义的语句无分号
  end
endmodule

例如对于图示门电路

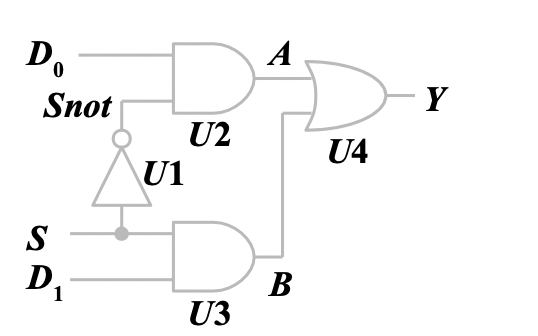
建立其 Verilog 模型

module mux2to1(output Y, input[1:0], input S);
  wire Snot, A, B;// 定义内部节点信号数据类型
  not U1(Snot, S);
  and U2(A,D[0], Snot);
  and U3(B,D[1],S);
  or U4(Y,A,B);
endmodule