一、组合逻辑电路分析

1. 定义

根据是否具有记忆功能，可以将数字逻辑电路分为组合逻辑电路和时序逻辑电路。

组合逻辑电路不具有记忆功能，任意时刻输出仅取决于此时的输入，与电路状态无关。

特点

信号单向传输，输出、输入之间无反馈延迟通路
无记忆功能，不含状态记忆元件

其电路结构可以抽象为

2. 分析方法

给定一个组合逻辑电路的电路图，分析其功能的过程称为组合逻辑电路的分析。一般的步骤为

写出输出端的函数表达式
对输出函数进行化简与变换
列出输出函数真值表
评述逻辑功能

例题

逻辑电路如图，分析其功能

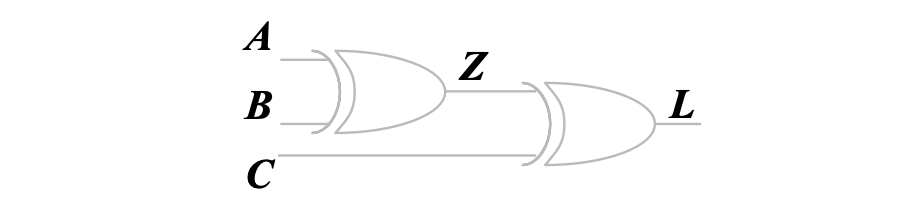
写出输出函数表达式并化简

列真值表

A	B	C	L
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

评述逻辑功能

由真值表可以看出，输入变量的取值中有奇数个 1 时， L 为 1 ，否则 L 为 0 ，电路具有为奇校验功能

二、组合逻辑电路设计

1. 定义

给定需要实现的逻辑功能，画出对应的组合逻辑电路的过程称为组合逻辑电路的设计。

2. 一般步骤

逻辑抽象：根据实际问题的因果关系确定输入、输出变量，并定义逻辑状态的含义
根据逻辑描述列出真值表
由真值表写出逻辑表达式
根据所采用的逻辑器件的类型，简化和变换逻辑表达式
画逻辑电路图

例题：

用与非门设计三变量多数表决器，其中 A 具有否决权

逻辑抽象

三个输入变量，分别为 A，B，C

一个输出变量 L，用于表示表决结果

记 0 为反对，1 为赞成

列出真值表

根据多数表决器的逻辑含义，真值表可以表示为

A	B	C	L
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	1

画出卡诺图

A\BC	00	01	11	10
0	0	0	0	0
1	0	1	1	1

画出两个圈，得到逻辑关系为

变换逻辑类型

要求使用与非门，因此用与非式来表示

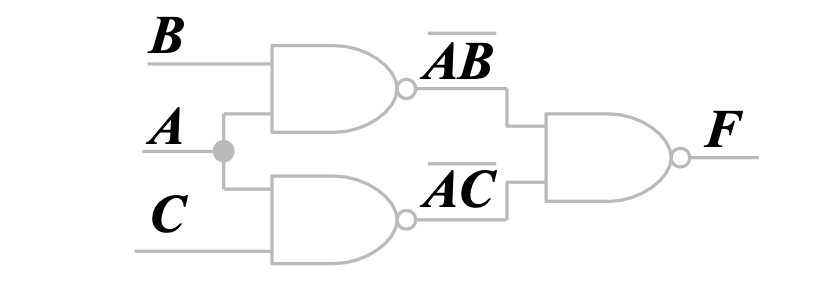
3. 优化

3.1 单输出电路优化

逻辑电路的与门，一般是由与非门和非门组成，因此与非门比与门的延迟小，成本低。在设计电路时，尽量使用与非门替代与门

3.2 多输出电路优化

需考虑共享相同乘积项，以减少逻辑门数目

3.3 多级逻辑电路

由于接口电路带负载能力有限，有时会对逻辑门输入端数量有要求。

如：限定逻辑门的扇入数为 3 实现

提取公因子为

电路图可以优化为

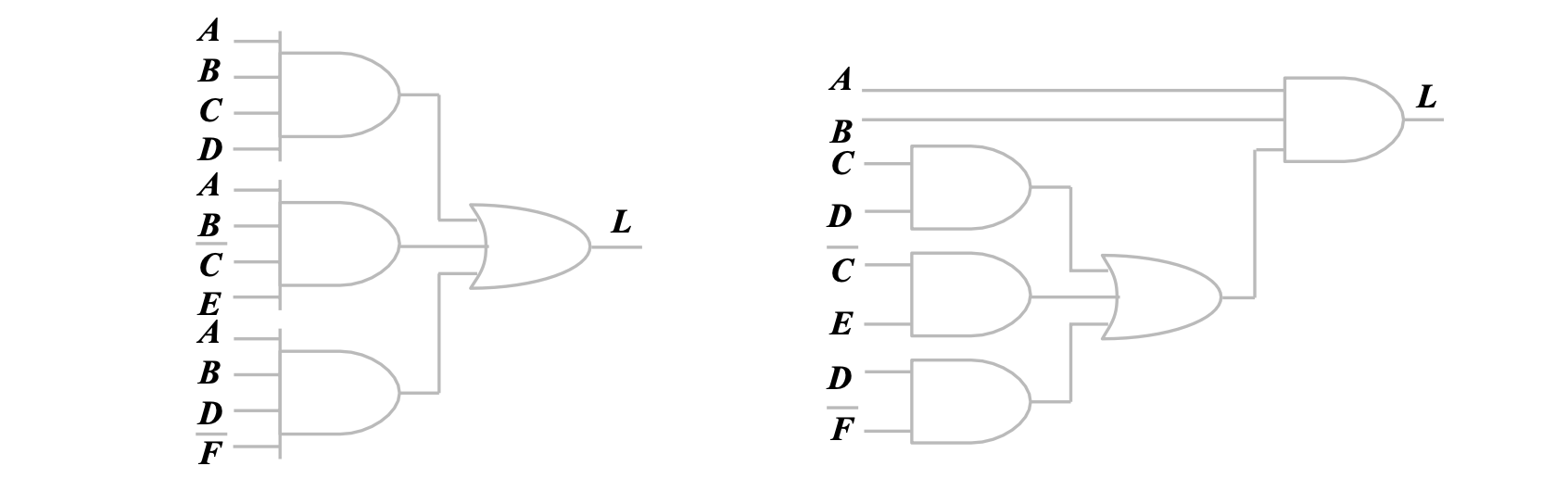
三、竞争与冒险

1. 产生竞争与冒险的原因

实际电路中，信号经过任何逻辑门都需要一定时间。不同路径上的逻辑门数量一般都不同，如果时序控制不妥，会导致错误输出，此现象叫电路的竞争冒险

例如逻辑电路，当和时都有

若使，同时，从理论上来说，在此变化瞬间，

但实际上，若前级电路时延有差异，使得滞后，则在瞬间会输出一个错误的，此时称电路出现了竞争冒险。

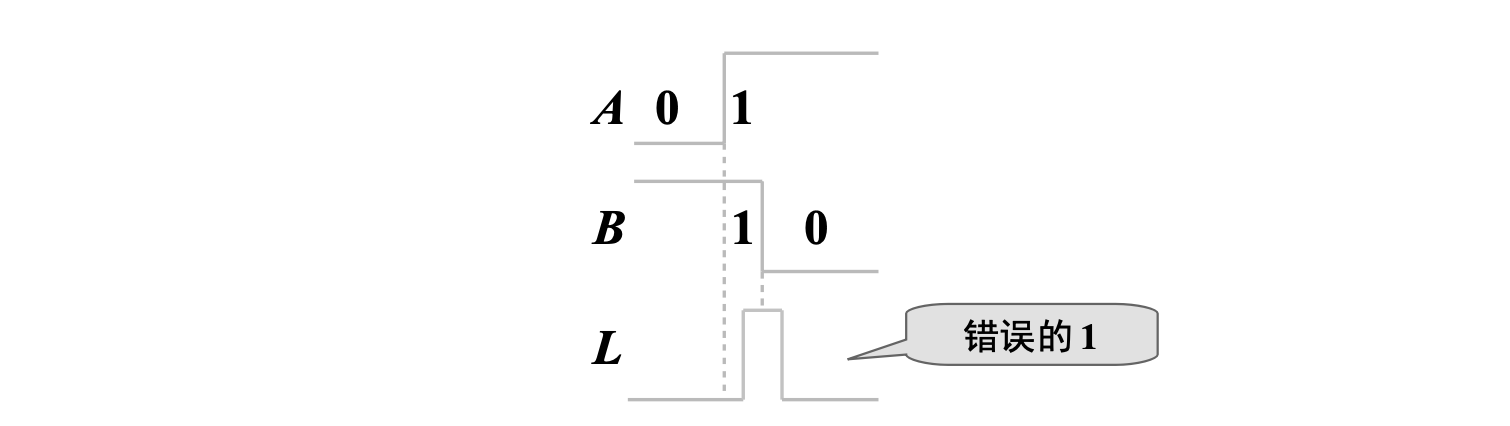
2. 竞争与冒险的定义

当逻辑门的两个输入端的信号，理论上同时向相反方向变化，而实际变化的时间却存在差异，导致产生错误脉冲的现象称为「竞争」

源自同一个信号的互反变量，引起逻辑门输入端两个信号取值变化方向相反，导致由于竞争而产生错误脉冲的现象称为「冒险」

由以上定义可知，冒险是竞争的上级概念。

3. 竞争与冒险的判断

3.1 代数法

检查是否存在具有竞争冒险条件的变量，即都存在
将其他变量的所有取值代入表达式，观察是否出现或

若出现，则可能产生错误 1，若出现，则可能产生错误 0

例

发现两变量存在原变量和反变量，可能存在竞争与冒险。先分析，代入的所有取值

，此时
，此时
，此时
，此时

因此 A 会产生竞争与冒险的错误 0

再分析，代入的所有取值

，此时
，此时
，此时
，此时

故不会产生竞争与冒险

3.2 卡诺图法

作卡诺图
画表达式中各与项的卡诺圈
观察，若发现两个卡诺圈相切，则该电路可能存在竞争与冒险

例

判断以下逻辑电路是否存在竞争与冒险

画出的卡诺图，并作出卡诺圈

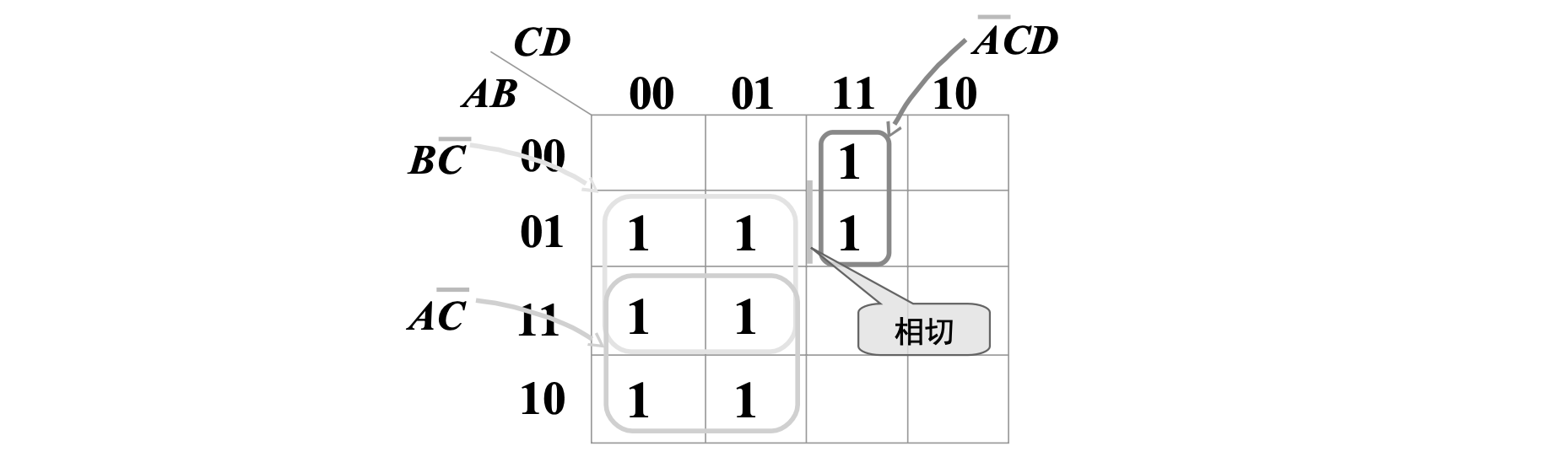
存在两个圈相切，相切在 $，，$ ，此时，的变化会产生错误

4 消除竞争与冒险的方法

4.1 增加冗余乘积项

若A在卡诺图中存在某两个卡诺圈相切，则用一个多余的卡诺圈将相切处相邻最小项圈起来，多余的卡诺圈对应与项就是要加入的冗余项。

例如对于

画出卡诺图，找出相切卡诺圈

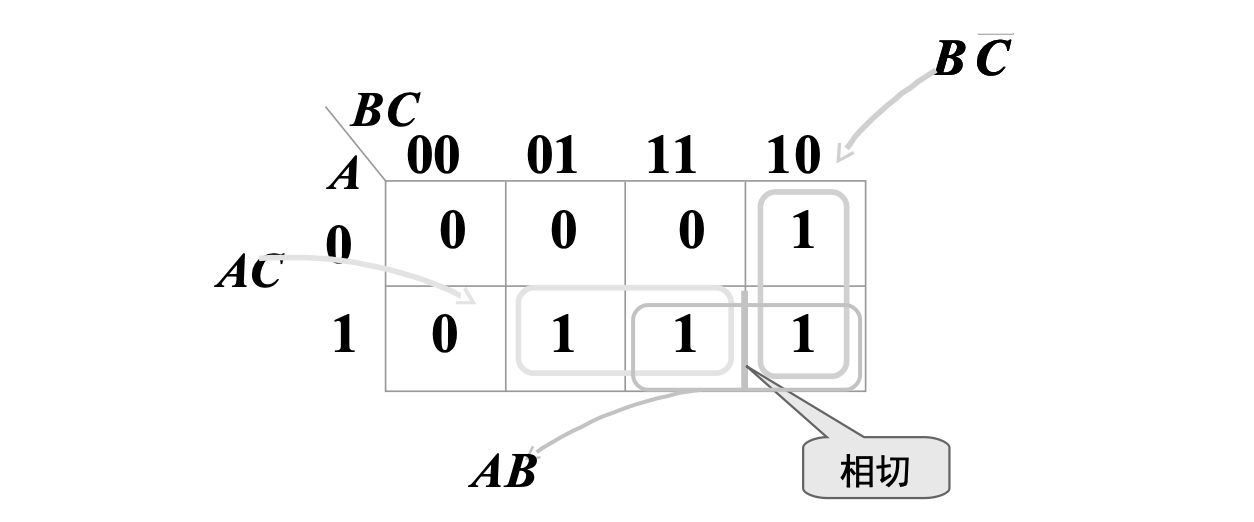
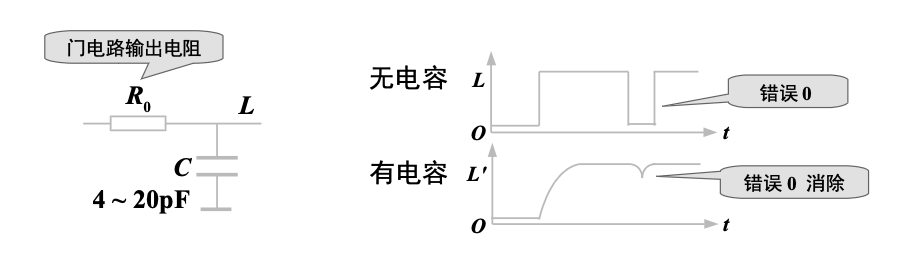
4.2 输出端并联电容器

若逻辑电路在较慢速度下工作，为了消去竞争冒险，可在输出端并联一电容器，使输出波形上升沿和下降沿变化较缓，对很窄的负跳变脉冲起平波作用

四、常用组合逻辑电路

常用组合逻辑电路被制成了中规模集成电路（MSI），广泛用于数字系统的设计中

1. 编码器

1.1 定义

编码与编码器

赋予二进制代码特定含义的过程称为编码。具有编码功能的逻辑电路称为编码器。编码器的逻辑功能就是将每一个需要编码的输入信号转变为不同的二进制的代码输出。

例如二进制编码器，有个带有编号的输入端，用个输出端对其进行编码

编码器的分类

普通编码器：只允许输入一个有效信号，否则输出混乱
有限编码器：允许同时输入多个有效信号，只对优先级高的进行编码

1.2 设计

以 4-2 线普通二进制编码器设计为例，有四个输入端，两个输出端，要求输入信号高电平有效

则其真值表可以表示为


1	0	0	0	1	1
0	1	0	0	1	0
0	0	1	0	0	1
0	0	0	1	0	0

则输出函数表达式可以表示为

根据输出函数画出逻辑电路

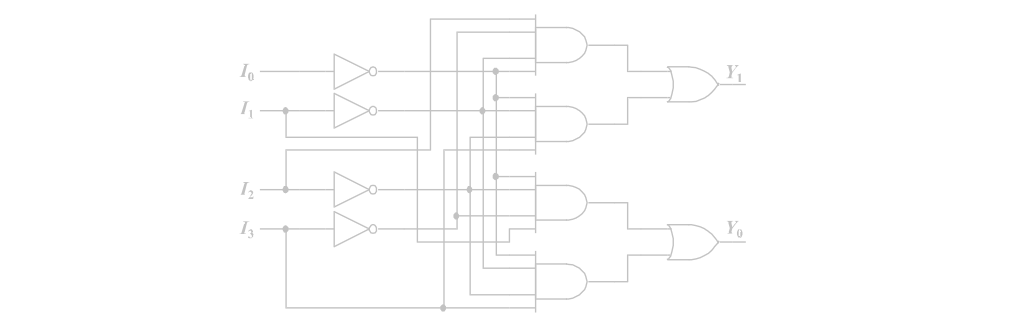
当输入端多个信号同时有效时，会产生输出混乱

1.3 典型编码器

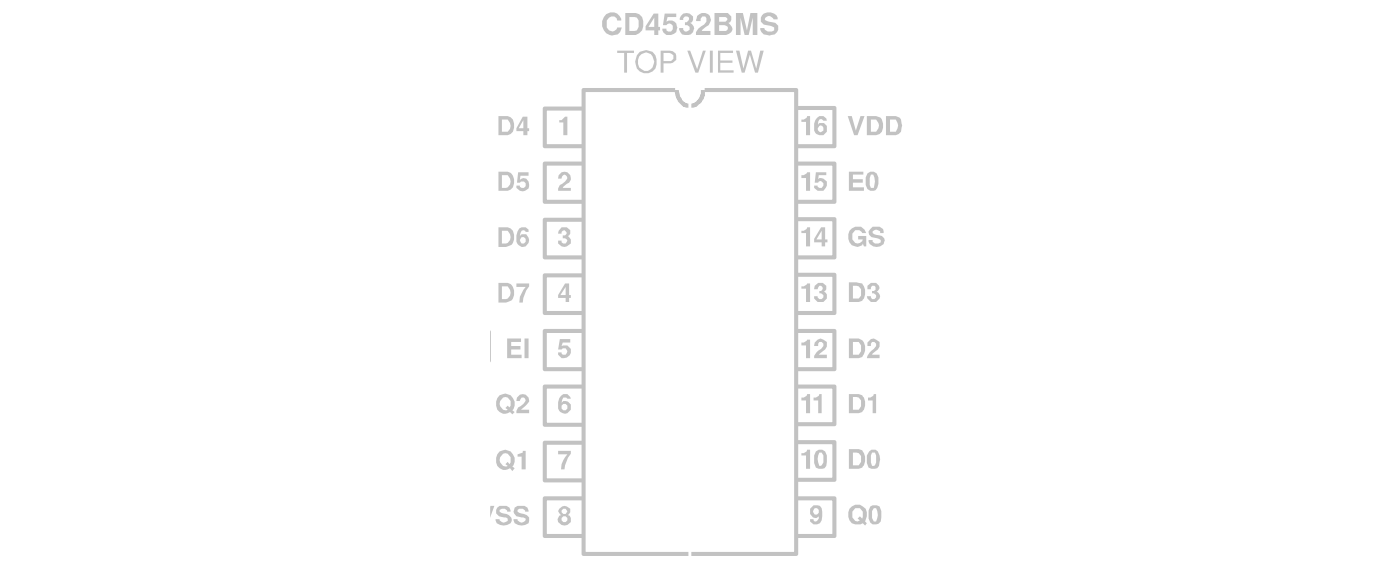
优先编码器 CD4532

8-3 优先二进制编码器，输入高电平有效

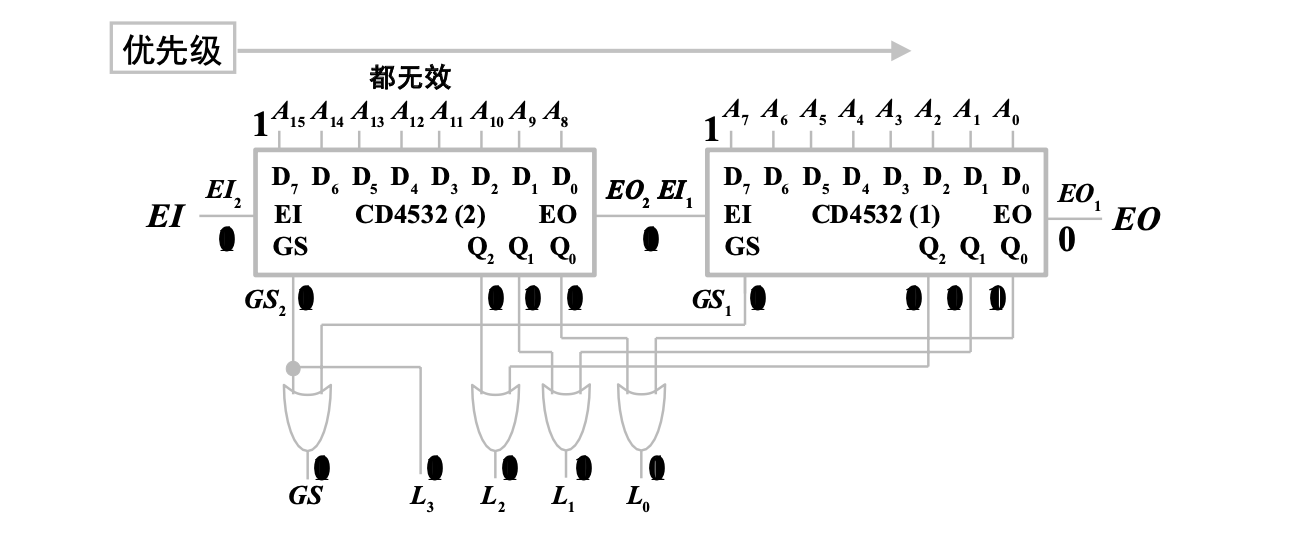
十六个引脚，八个信号输入端，一个输入使能端，三个编码输出端，一个输出使能端，一个引脚标志编码器工作状态，两个供电端口

两片 CD4532 构成 16-4 线优先编码器

思路：一片 CD4532 处理高八位，另外一片处理低八位

若高位片工作，则最高输出为为 1，剩下三位用高位片输出；若高位片不工作，最高输出为 0，剩下三位用低位片输出。

由此可以得到

2. 译码器

2.1 定义

译码与译码器

将二进制码翻译成代表某一特定含义的信号的过程称为「译码」，具有译码功能的逻辑电路称为译码器

例如二进制译码器，有个输入端输入位代码，用个输出端表示二进制数

译码器的分类

唯一地址译码器：将输入代码转换为与之对应的唯一有效信号
代码变换器：将一种代码转换为另一种代码

常见的译码器有：二进制译码器、BCD 译码器和显示译码器。

2.2 设计

以 2-4 线二进制译码器设计为例，有两个输入端，四个输出端，要求输入信号低电平有效

则其真值表可以表示为


0	0	0	1	1	1
0	1	1	0	1	1
1	0	1	1	0	1
1	1	1	1	1	0

则输出函数表达式可以表示为

根据输出函数画出逻辑电路

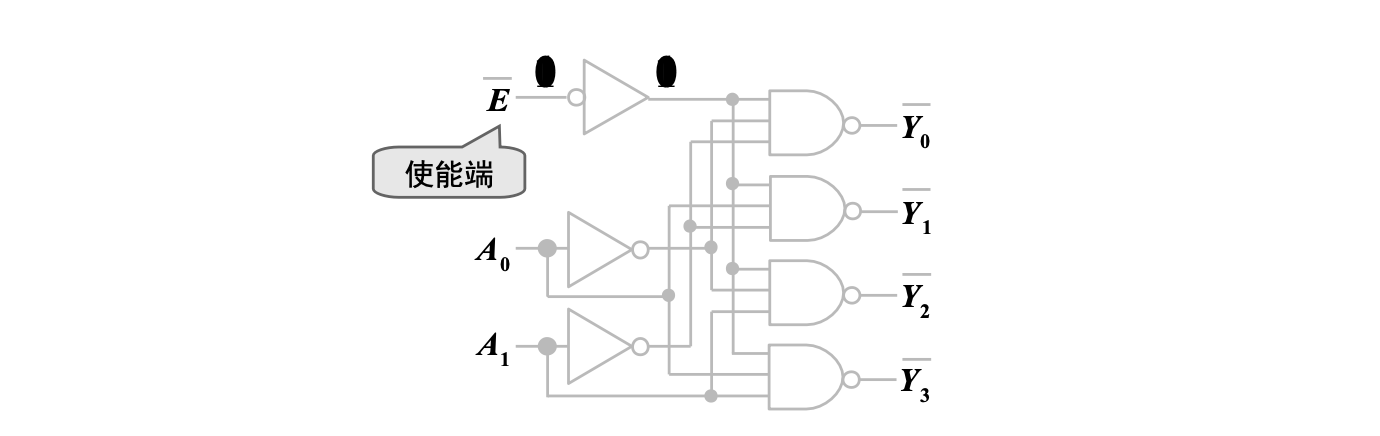
2.3 典型译码器

74HC139 译码器

2-4 线二进制译码器，两个输入端，四个输出端，一个低电平有效输入使能端

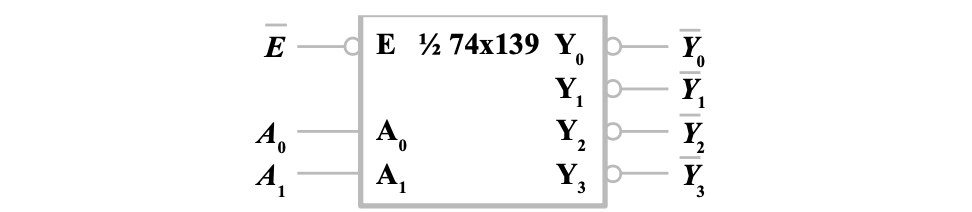
74HC138 译码器

3-8线二进制译码器，三个输入端，八个输出端，三个使能端，当时使能有效

其逻辑符号为

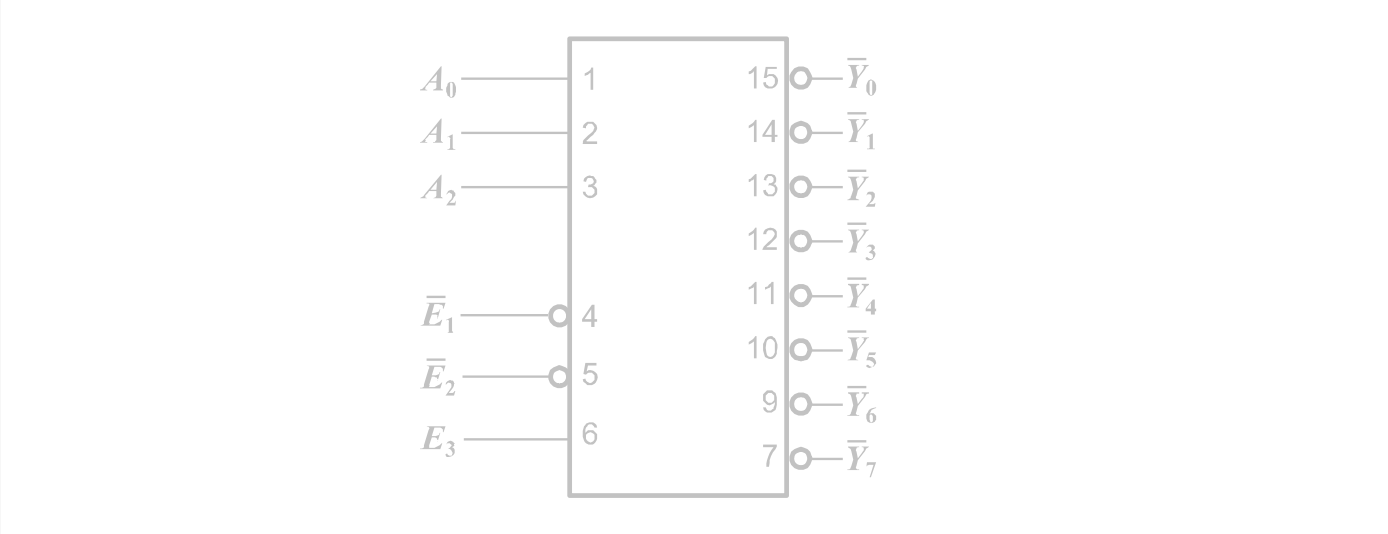
其引脚图为

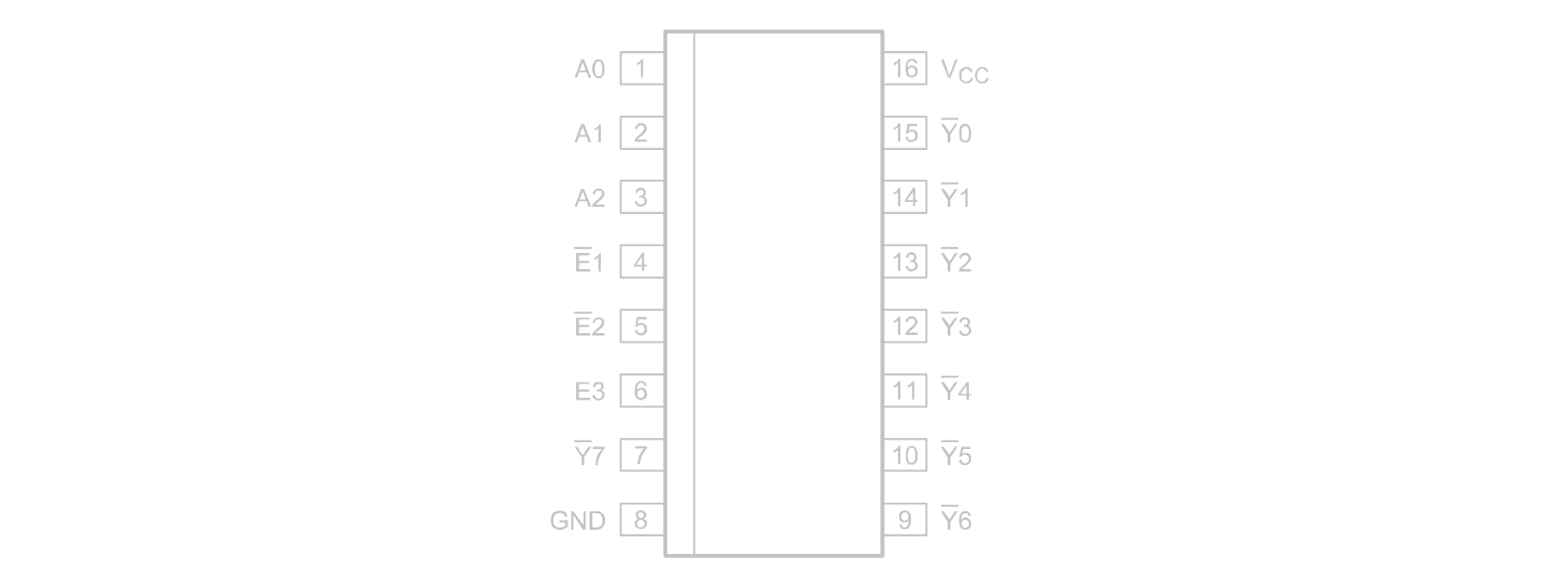
位扩展

可以用两片 3-8 译码器扩展为 4-16 译码器

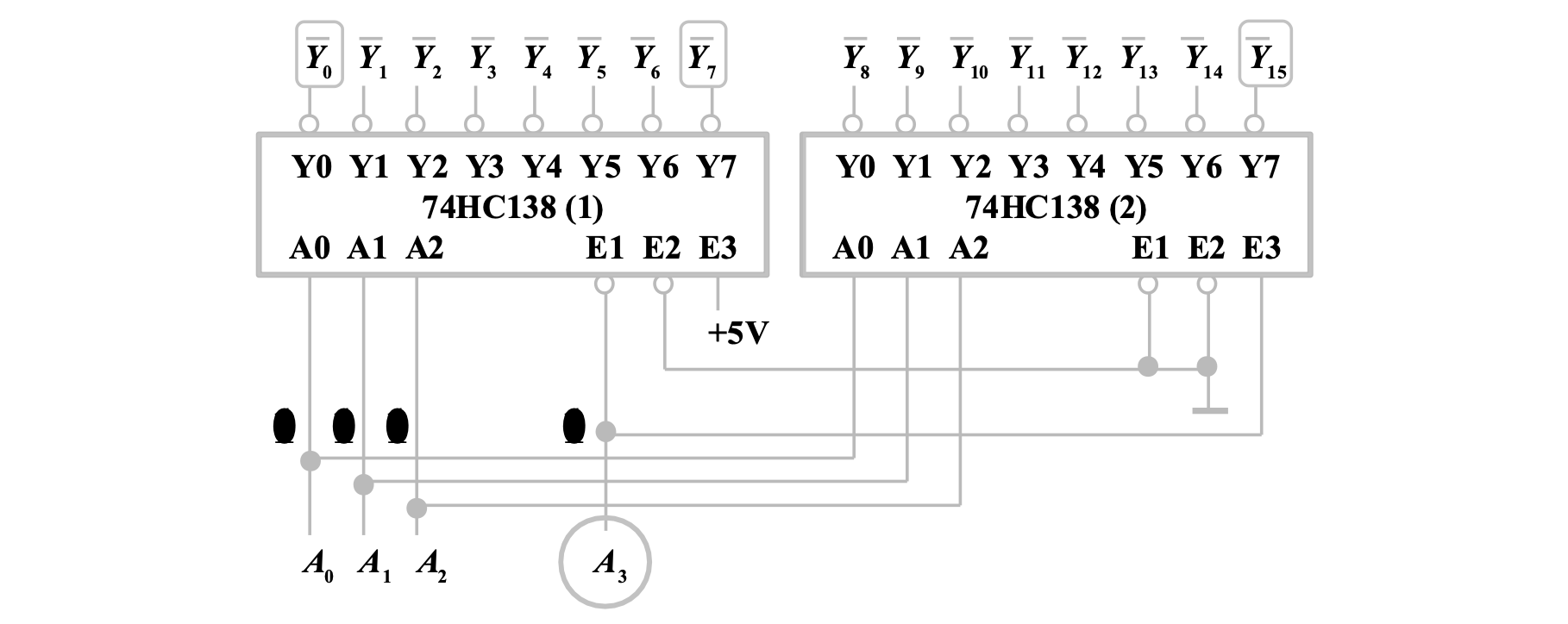
组合逻辑功能

74138 的输出是 3 变量最小项之补，而任何组合逻辑函数均可变换为若干最小项之或，利用 74138 输出可方便实现组合逻辑功能

例如要实现函数

因此只需要在四个输出端接一个与非门即可

数据分配器

能将从数据分时送到多个不同的通道上去的逻辑电路称为「数据分配器」，相当于多输出的单刀多掷开关。输入一串通道选择信号，就可以将数据送到对应编码的通道。

数据分配器可用唯一地址译码器实现，将输入信号从使能端输入即可

74HC42 译码器

BCD 译码器，能将 8421 BCD 码译成 10 个状态，输出端低电平有效


0	0	0	0	0	1	1	1	1	1	1	1	1	1
0	0	0	1	1	0	1	1	1	1	1	1	1	1
0	0	1	0	1	1	0	1	1	1	1	1	1	1
0	0	1	1	1	1	1	0	1	1	1	1	1	1
0	1	0	0	1	1	1	1	0	1	1	1	1	1
0	1	0	1	1	1	1	1	1	0	1	1	1	1
0	1	1	0	1	1	1	1	1	1	0	1	1	1
0	1	1	1	1	1	1	1	1	1	1	0	1	1
1	0	0	0	1	1	1	1	1	1	1	1	0	1
1	0	0	1	1	1	1	1	1	1	1	1	1	0
1	0	1	0	1	1	1	1	1	1	1	1	1	1
1	0	1	1	1	1	1	1	1	1	1	1	1	1
1	1	0	0	1	1	1	1	1	1	1	1	1	1
1	1	0	1	1	1	1	1	1	1	1	1	1	1
1	1	1	0	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1	1	1	1

BCD 码之外的 6 个伪码（1010 $），$ Y_0\sim Y_9$ 均为高电平

显示译码器

用发光二极管可以构成显示数字的阵列，常见的 LED 显示器为七段，每一段对应一个发光二极管，用字母 ABCDEFG 来表示

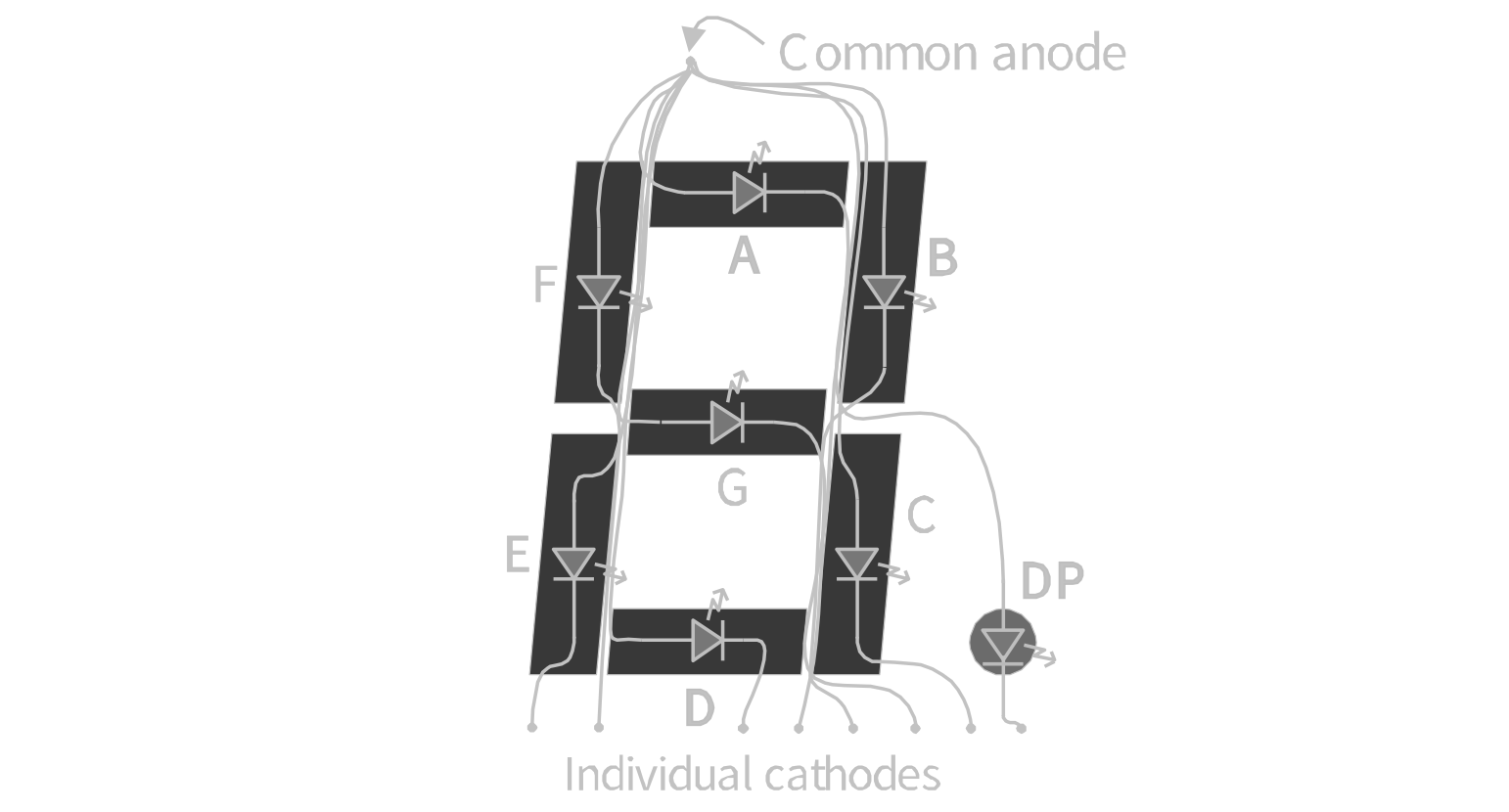
显示器可以分为共阳极和共阴极两种

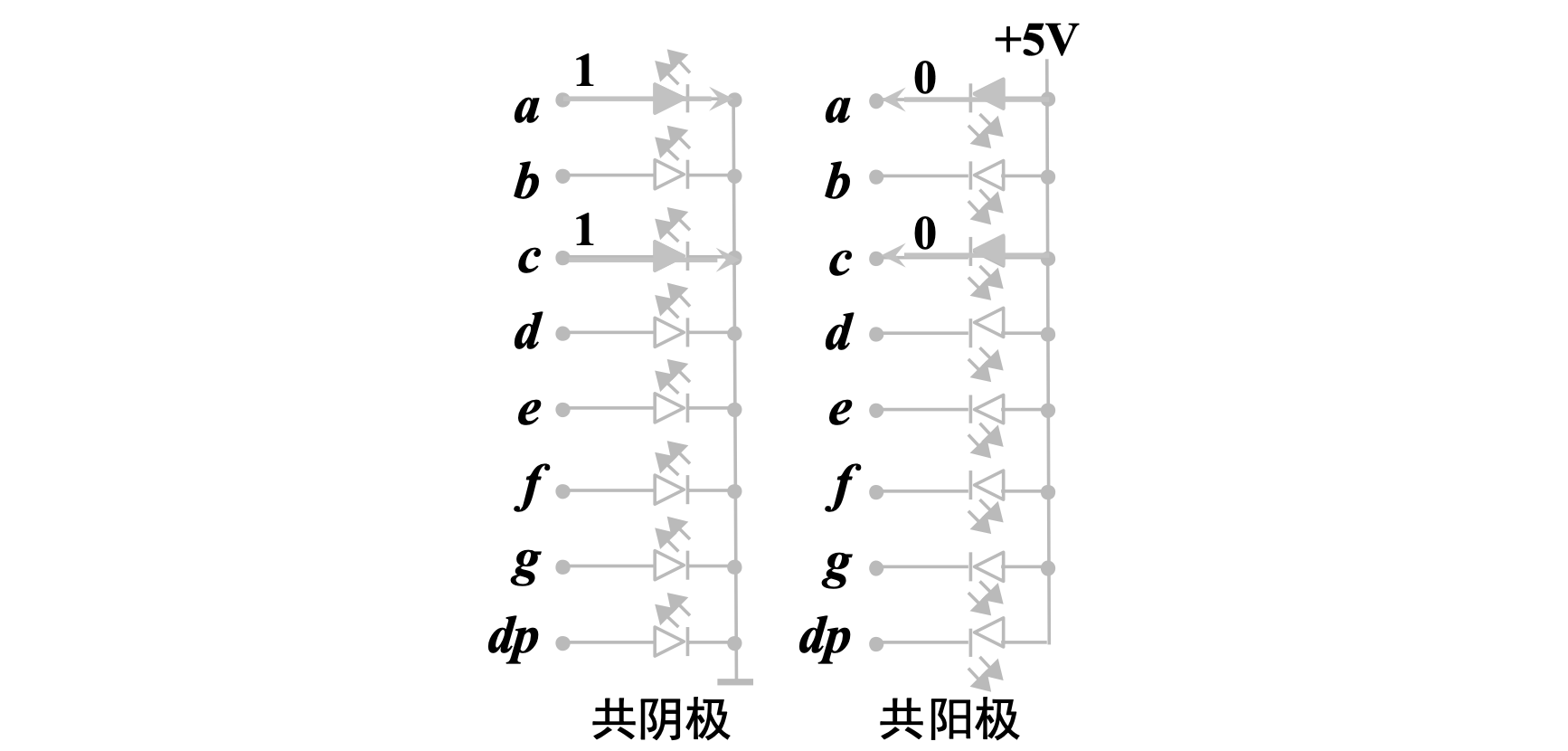
为了使 LED 显示不同数字，就要为 LED 提供段码（或称字型码），如对于共阴极 LED 显示器，当引脚为高电平时，LED 发光

74HC4511

74HC74511 是一种 CMOS 七段显示译码器，其功能表可以表示为


0	0	0	1	1	1	1	1	1	0
0	0	1	0	1	1	0	0	0	0
0	1	0	1	1	0	1	1	0	1
0	1	1	1	1	1	1	0	0	1
1	0	0	0	1	1	0	0	1	1
1	0	1	1	0	1	1	0	1	1
1	1	1	1	1	1	0	0	0	0

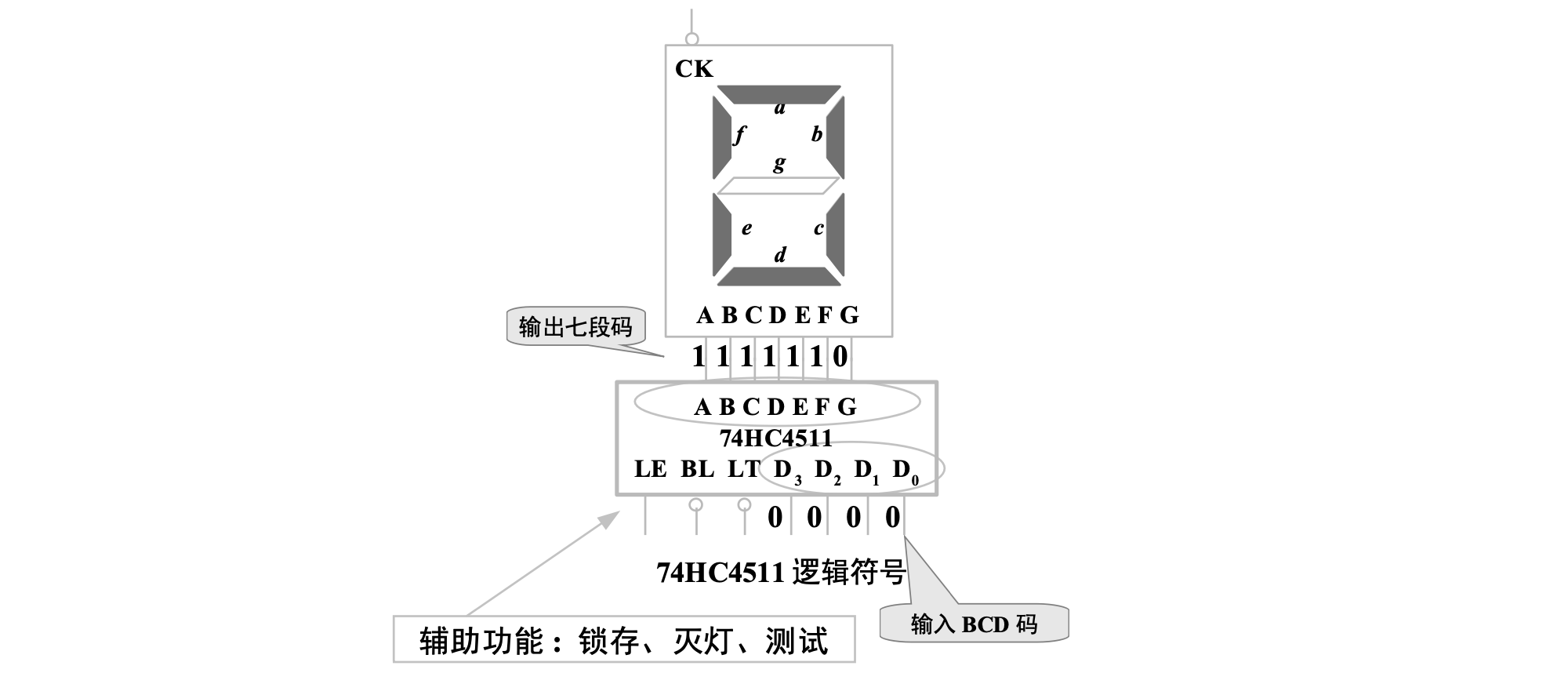
实际上，显示译码器与显示器之间通常使用阻值为的电阻进行连接。

若使用数据分配器，则可以利用人的视觉暂留时间，使多个显示器轮流显示，在人眼看来，所有显示器均显示稳定数字

3. 数据选择器

3.1 定义

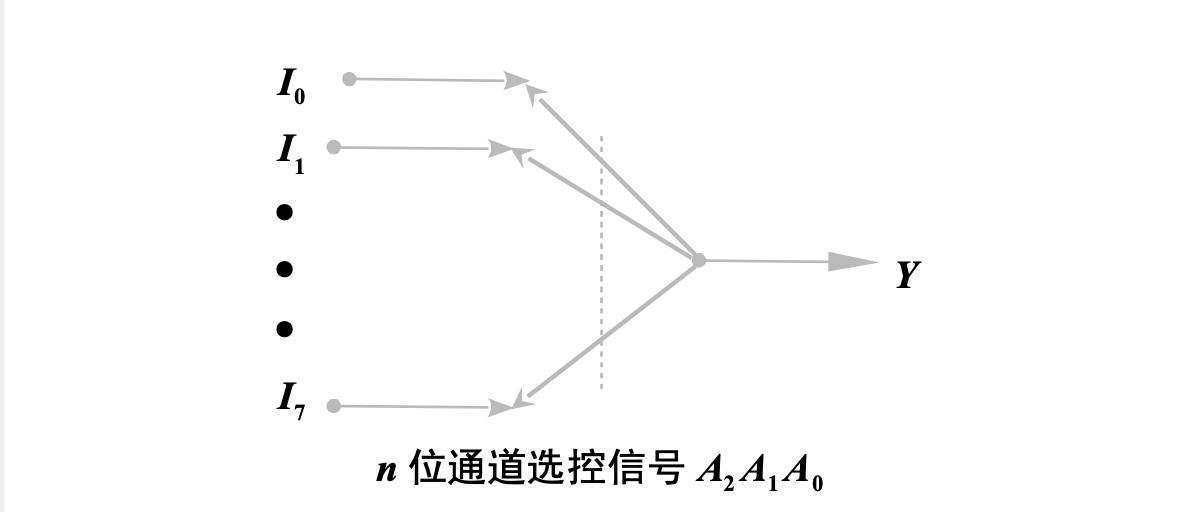
在位通道选控信号的作用下，分时传输多通道数据至公共通道的逻辑功能称为「数据选择」，相当于多个输入端的单刀多掷开关。

能实现数据选择功能的逻辑电路叫做「数据选择器」（Multiplexer），简称 MUX

3.2 设计

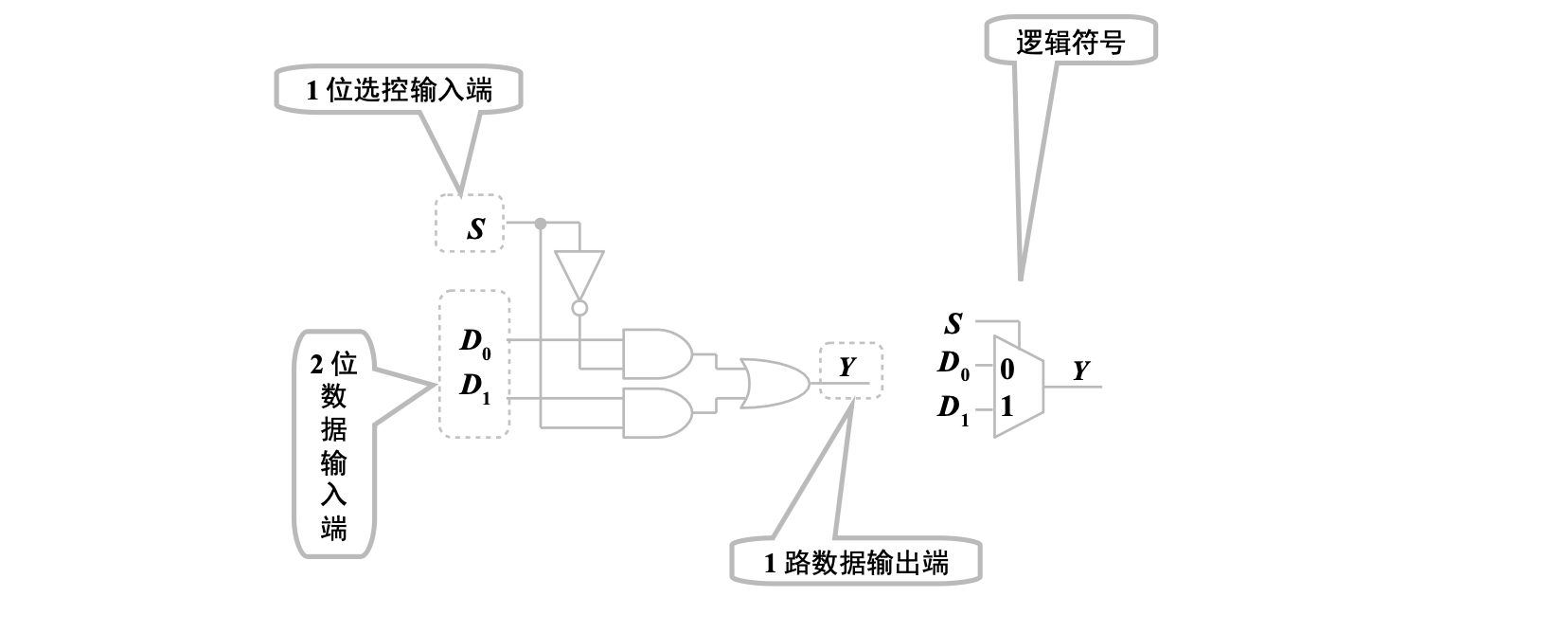
2 选 1 数据选择器

最基本的数据选择器就是 2 选 1 数据选择器，由 2 位数据输入端，1 位数据输出端和 1 位选控输入端组成

4 选 1 数据选择器

由 3 个 2 选 1 数据选择器构成 4 选 1 数据选择器，由 4 位数据输入端，1 位数据输出端和 2 位选控输入端组成

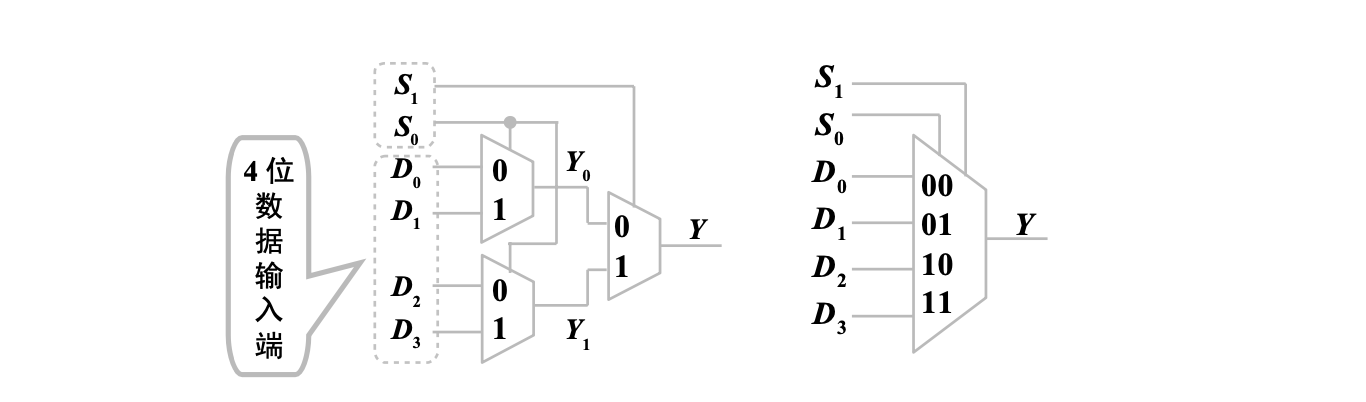
得到逻辑表达式

数据选择器同样可以用来表达逻辑函数，比如说表示，可以将，则输出函数就为

利用数据选择器表达函数的一般步骤

具有个控制变量的 MUX，实现个变量的逻辑函数，有两种情况：

若

将目标函数个变量分配给 MUX 个控制端
将目标函数表示成最小项形式
若目标函数有最小项，则选择器对应的接 1 ，其他接 0

若

在目标函数个变量中选个作为选择器的选控端
写出选择器输出表达式
比较目标函数的最小项表达式，以便确定

数据选择器和译码器实现逻辑函数比较

相同点:
1. 直接用最小项表达式，不用化简逻辑函数
2. 电路简单，易于检查和排除故障
不同点:
1. 一个译码器可同时实现多个逻辑函数，但变量数不能超过地址端数量
2. 一个选择器只能实现一个逻辑函数，变量数可超过选控端数量

显示查找表

将数据选择器的每个输入端接在预先写入的数据表上，此时构成了「显示查找表」（Look-up table），简称 LUT。 LUT 的实质是存储器加选择器，可以以真值表的形式实现逻辑函数

在查找表中存放对应的存储单元，即可实现逻辑函数的功能，实现方法就是利用数据选择器表达函数。

74HC151

74HC151 是一种 8 选 1 集成电路数据选择器，符号为

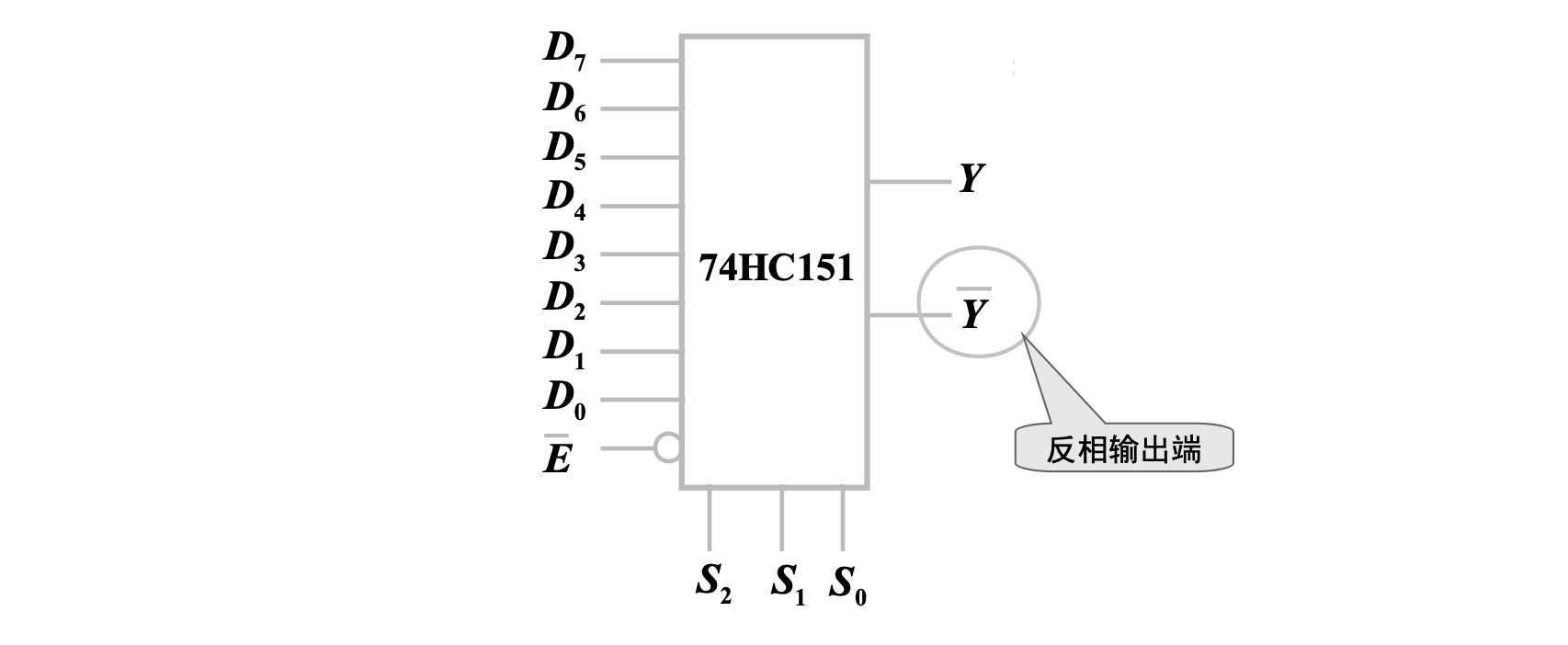
使能有效后输出表达式为

并行数据到串行数据的转换

多根线上的多位数据称为「并行数据」，一根线上分时表示的多位数据称为「串行数据」，控制，可将数据串行输出

4. 数值比较器

对两个数字进行比较，以判断其大小的逻辑电路叫做「数值比较器」。

4.1 一位数值比较器

对于一位数值比较器，有两个输入端，三个输出端，分别为

真值表可以表示为


0	0	0	0	1
0	1	0	1	0
1	0	1	0	0
1	1	0	0	1

输出表达式为

4.2 多位数值比较器

用一位数值比较器设计多位数值比较器的原则，若高位和不等，即可得其结果，无需再比较低位和若高位相等，再比较低位，因此二位真值表可以表示为


1	0	0
0	1	0
1	0	0
0	1	0
0	0	1

其逻辑表达式为

因此可以用一位数值比较器和必要的逻辑门构成两位数值比较器

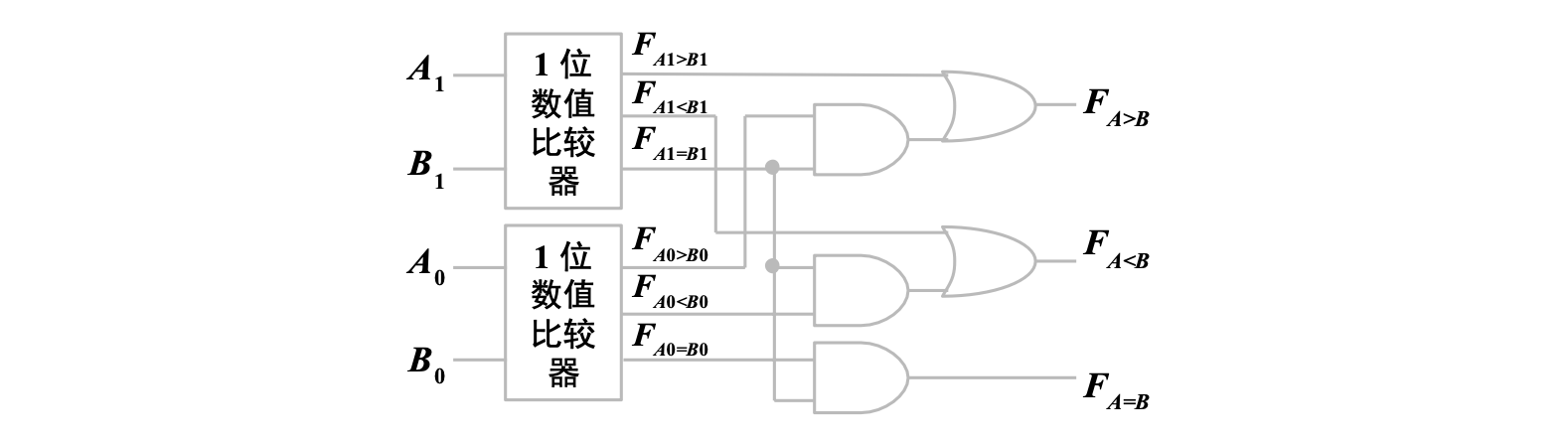
5. 算术运算电路

5.1 半加器和全加器

加法器分为半加器和全加器两种。在两个 1 位二进制数相加时，不考虑低位来的进位的加法器叫做「半加器」，而考虑低位进位的加法器叫做「全加器」，其逻辑符号为

半加器

根据半加器的功能描述，可以列出真值表


0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

得到逻辑表达式

因此电路如图

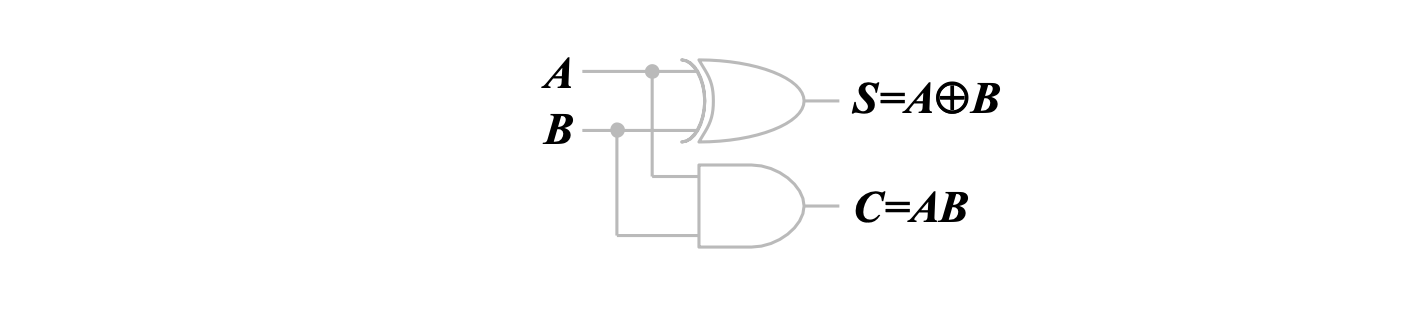
全加器

全加器需要多一个输入端考虑低位进位，因此其真值表为


0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

从真值表得到逻辑表达式并进行化简

因此全加器的内部结构为

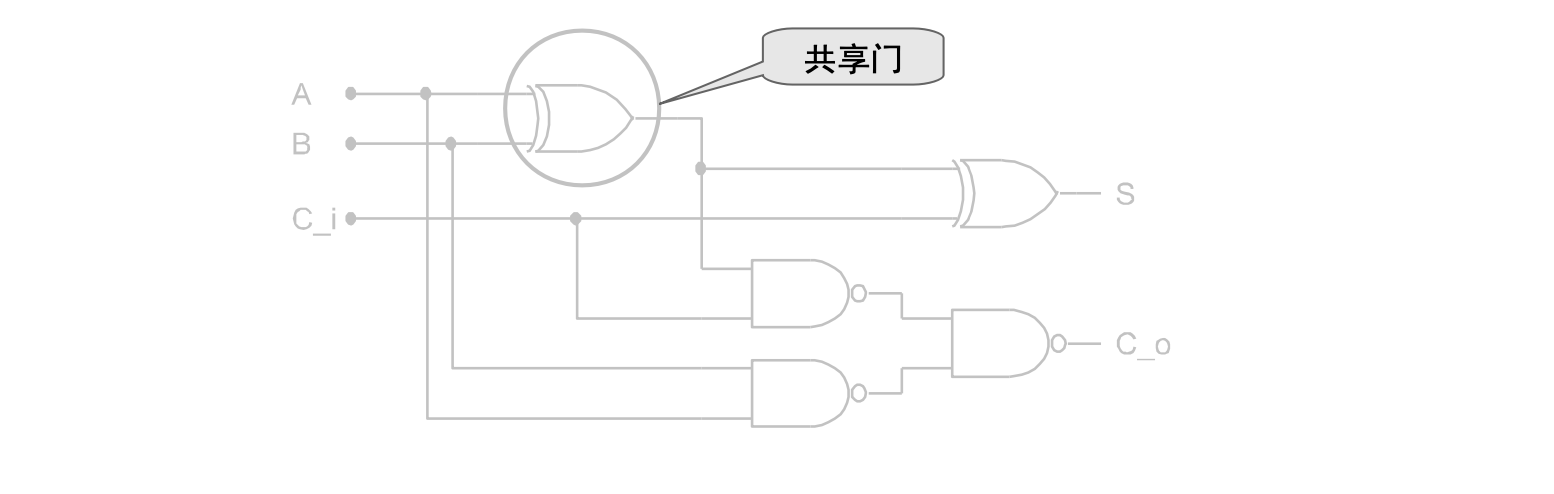
也可以由两个半加器构成全加器电路

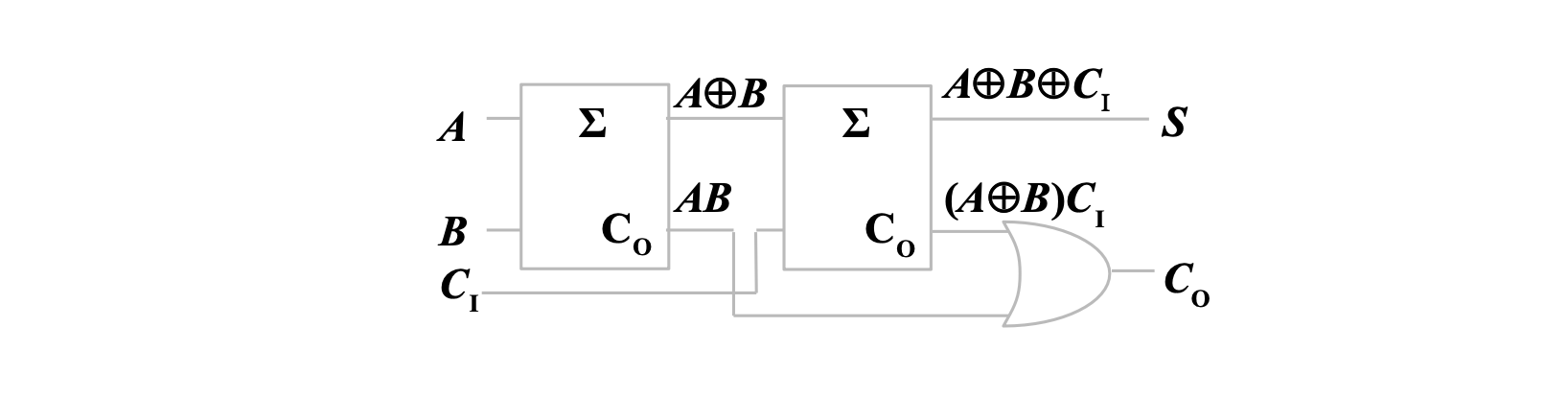
注意到，对于全加器的，ABC 有奇数个 1 时 S 为 1，而 ABC 有偶数个 1 时 S 为 0，S 可作为三位二进制码的奇偶校验器

5.2 多位数加法器

串行进位加法器

将多个 1 位全加器串行，可以实现多位二进制数的串行进位加法器

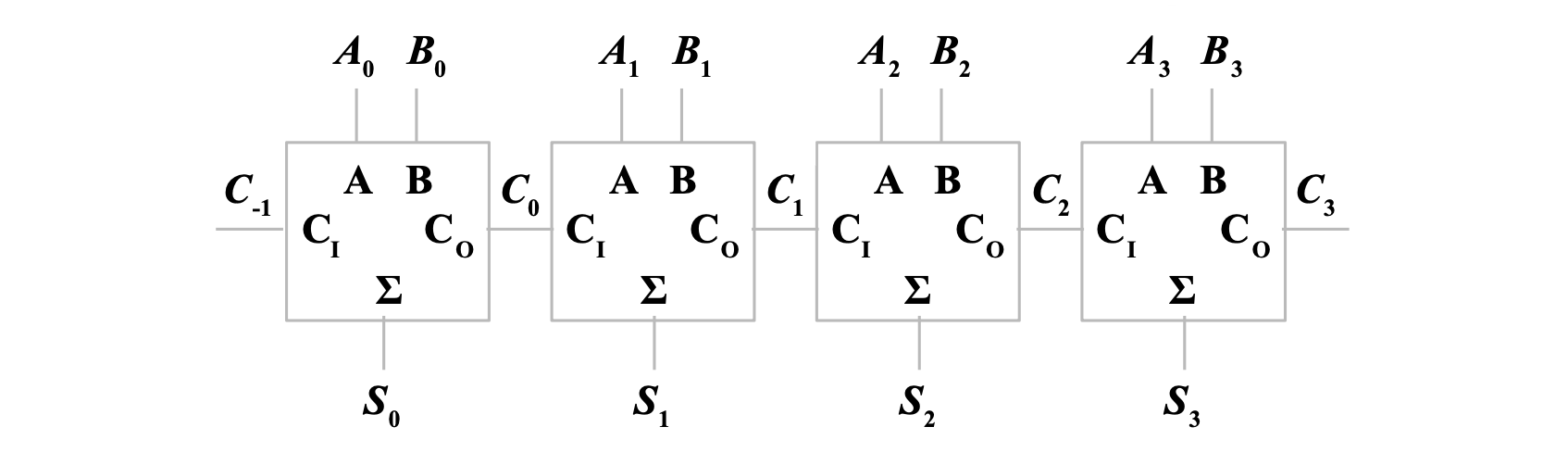
串行进位加法器电路简单，但前级产生进位后，后级加法才有效，位数越多，速度越慢

超前进位加法器

对于进位电路，定义第位为，第位进位信号为，显然有关系

定义两个中间变量 $和$

每次运算得到和都需要一个时间延迟，即

则原来串行进位的进位过程可以表示为

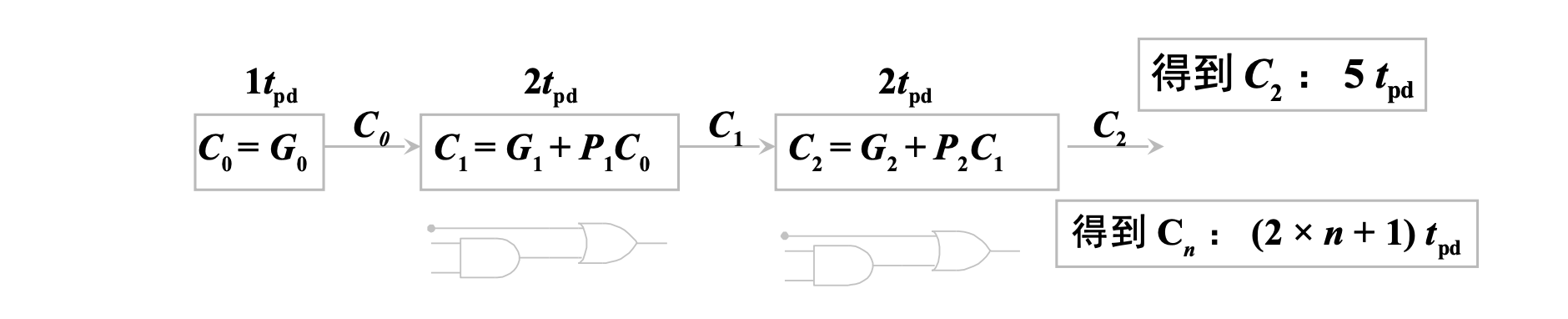
可以发现，随着倍数增加，延迟越来越大。为了改进这个问题，我们希望在输入每位的加数和被加数时，同时获得该位全加的进位信号，而无需等待低位的进位

根据上面分析进位过程的递推式，以三位进位信号为例

对于任意一级进位信号，只需要最多三级延迟，分别是

产生所有中间信号和
对信号做与运算
对信号做或运算

综上，超前进位加法器以增加硬件成本为代价，获得极高的计算速度

5.3 无符号数减法运算

对于四位无符号数减法运算，以原码形式输出结果，减法运算可以表示为

符号数之差有正有负，输出的 4 位数只表示值位，需扩展符号位
- 若为正数，四位输出是其绝对值
- 若为负数，四位输出是其绝对值关于 2 的补，再求补，得其绝对值
可采用异或门根据正负判断结果来控制是否对值位求补

分析两种不同情况

差为非负

时

设，则

无符号数减法的最高进位之反表示借位，借位可用于差的符号位扩展，时，借位为，即差为正数

差为负

时

设，则

借位为 1 ，即差为负数，因此需对值位求补，得到原码形式的值位，即

六、Verilog 描述组合逻辑电路

组合逻辑电路的行为级描述一般使用

assign 结构：连续赋值语句
always 结构：过程赋值语句
条件语句（if-else）
多路分支语句（case-endcase）
for 循环语句等

if (condition_expr1) true_statement1;
else if (condition_expr2) true_statement2; 
else if (condition_expr3) true_statement3; 
...
else default_statement;

for (initial_assignment; condition; step_assignment) 
    statement;

case (case_expr)
    item_expr1: statement1;
    item_expr2: statement2;
    ...
    default: default_statement;
endcase


0	0	0	0	0	1	1	1	1	1	1	1	1	1
0	0	0	1	1	0	1	1	1	1	1	1	1	1
0	0	1	0	1	1	0	1	1	1	1	1	1	1
0	0	1	1	1	1	1	0	1	1	1	1	1	1
0	1	0	0	1	1	1	1	0	1	1	1	1	1
0	1	0	1	1	1	1	1	1	0	1	1	1	1
0	1	1	0	1	1	1	1	1	1	0	1	1	1
0	1	1	1	1	1	1	1	1	1	1	0	1	1
1	0	0	0	1	1	1	1	1	1	1	1	0	1
1	0	0	1	1	1	1	1	1	1	1	1	1	0
1	0	1	0	1	1	1	1	1	1	1	1	1	1
1	0	1	1	1	1	1	1	1	1	1	1	1	1
1	1	0	0	1	1	1	1	1	1	1	1	1	1
1	1	0	1	1	1	1	1	1	1	1	1	1	1
1	1	1	0	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1	1	1	1


0	0	0	1	1	1	1	1	1	0
0	0	1	0	1	1	0	0	0	0
0	1	0	1	1	0	1	1	0	1
0	1	1	1	1	1	1	0	0	1
1	0	0	0	1	1	0	0	1	1
1	0	1	1	0	1	1	0	1	1
1	1	1	1	1	1	0	0	0	0


0	0	0	0	0	1	1	1	1	1	1	1	1	1
0	0	0	1	1	0	1	1	1	1	1	1	1	1
0	0	1	0	1	1	0	1	1	1	1	1	1	1
0	0	1	1	1	1	1	0	1	1	1	1	1	1
0	1	0	0	1	1	1	1	0	1	1	1	1	1
0	1	0	1	1	1	1	1	1	0	1	1	1	1
0	1	1	0	1	1	1	1	1	1	0	1	1	1
0	1	1	1	1	1	1	1	1	1	1	0	1	1
1	0	0	0	1	1	1	1	1	1	1	1	0	1
1	0	0	1	1	1	1	1	1	1	1	1	1	0
1	0	1	0	1	1	1	1	1	1	1	1	1	1
1	0	1	1	1	1	1	1	1	1	1	1	1	1
1	1	0	0	1	1	1	1	1	1	1	1	1	1
1	1	0	1	1	1	1	1	1	1	1	1	1	1
1	1	1	0	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1	1	1	1


0	0	0	1	1	1	1	1	1	0
0	0	1	0	1	1	0	0	0	0
0	1	0	1	1	0	1	1	0	1
0	1	1	1	1	1	1	0	0	1
1	0	0	0	1	1	0	0	1	1
1	0	1	1	0	1	1	0	1	1
1	1	1	1	1	1	0	0	0	0


0	0	0	0	0	1	1	1	1	1	1	1	1	1
0	0	0	1	1	0	1	1	1	1	1	1	1	1
0	0	1	0	1	1	0	1	1	1	1	1	1	1
0	0	1	1	1	1	1	0	1	1	1	1	1	1
0	1	0	0	1	1	1	1	0	1	1	1	1	1
0	1	0	1	1	1	1	1	1	0	1	1	1	1
0	1	1	0	1	1	1	1	1	1	0	1	1	1
0	1	1	1	1	1	1	1	1	1	1	0	1	1
1	0	0	0	1	1	1	1	1	1	1	1	0	1
1	0	0	1	1	1	1	1	1	1	1	1	1	0
1	0	1	0	1	1	1	1	1	1	1	1	1	1
1	0	1	1	1	1	1	1	1	1	1	1	1	1
1	1	0	0	1	1	1	1	1	1	1	1	1	1
1	1	0	1	1	1	1	1	1	1	1	1	1	1
1	1	1	0	1	1	1	1	1	1	1	1	1	1
1	1	1	1	1	1	1	1	1	1	1	1	1	1


0	0	0	1	1	1	1	1	1	0
0	0	1	0	1	1	0	0	0	0
0	1	0	1	1	0	1	1	0	1
0	1	1	1	1	1	1	0	0	1
1	0	0	0	1	1	0	0	1	1
1	0	1	1	0	1	1	0	1	1
1	1	1	1	1	1	0	0	0	0