一、基本建模

状态空间模型（State Space Models）是一种数学模型，用于描述动态系统的演化。它通过一组数学方程来表示系统的状态随时间的变化。状态空间模型广泛应用于工程、物理、经济学、生物学等领域，用于系统分析、控制设计、信号处理和时间序列分析等。

状态空间模型理论认为，对于一个系统而言，我们需要关注三个部分：输入，输出和状态。在此将输入记为，输出记为。

系统处于某状态时，系统在一定的输入下会给出一定的输出。显然系统的状态不同，势必会影响输出和输入的映射关系，因此我们需要对状态进行量化。

系统的状态可以用一组变量来表述，称这些变量为为内部状态，记为向量。这些变量通常不直接可观测，但它们会随时间演化，且满足一定的规律。

二、方程分析

状态空间模型主要包括两部分：状态方程和观测方程。

状态方程描述了系统内部状态的演化。状态方程通常表示为一阶微分方程（连续时间系统）或差分方程（离散时间系统），表达形式如下：

对于连续时间系统有

而对于离散时间系统

其中，或为当前时刻的内部状态，而或为此时的外部输入，和为系统本身的参数。

由于系统的状态不一定能被观测得到，但是系统在指定状态和输入下的输出是确定的，因此可以通过某些输出来间接获得状态信息。观测方程描述了如何从系统的内部状态得到可以观测到的输出。表达形式如下：

对于连续时间系统有

离散时间系统有

其中，或表示系统输出，和是系统参数，或表示观测噪声。建立系统状态方程的过程，本质上就是在求解系统的各参数。

如图给出一个弹簧-质量-阻尼系统。图中，质量为的物块被进度系数为的弹簧固定，同时物块收到大小为的摩擦力。对于此系统而言，很容易建立一个状态方程模型。其中，令施加在物块上垂直向下的力为输入，物块的垂直位移为系统的输出，而物块本身的速度，加速度等其他物理量，就是此系统的状态了。

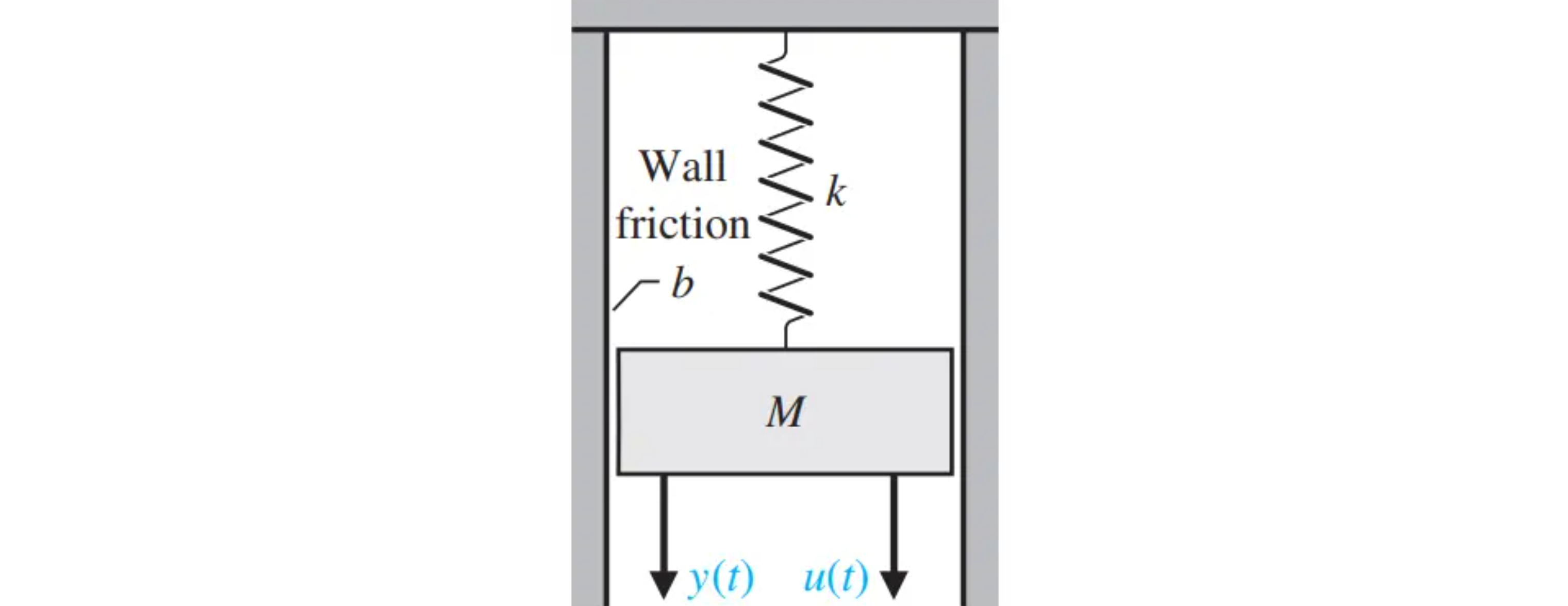
Pasted image 20240229223200.png

若设物块的位移（输出）本身和物块的速度作为系统的状态，分别记为和，则二者构成了一个内部状态向量

根据牛顿第一定理，显然可以列出微分方程

由此可以建立状态方程。这是一个连续时间系统，所以我们首先求解内部状态向量对时间的导数

整理成状态方程的格式

同理可以得到系统的观测方程

在深度学习的语境下，状态空间模型经常用于处理序列数据，如时间序列分析、自然语言处理、语音识别等领域。这些模型通过引入隐藏状态来捕捉数据中的时间动态性和依赖关系。与其他常规的状态空间模型不同的是，在这种设置中，观测方程描述的是如何只从隐藏状态生成观测数据，而没有直接从输入到输出的项。