一、时序逻辑电路的基本概念

1. 时序逻辑电路的引入

时序逻辑电路是除了组合逻辑电路外的另一大数字电路形式。其最大的不同在于，时序逻辑电路内部存在锁存器或触发器，因而存在各种各样的「状态」，这些状态与输入进行交互，产生各种各样的输出。一个典型的时序逻辑电路就是电梯的控制电路。控制电路根据电梯内和各楼层入口处按键的输入信号，以及电梯当前的现态，来决定电梯的激励信号是上升还是下降，同时还会显示输出现态。控制电路须记忆当前所处的楼层现态，以及即将达到的楼层次态。

对于时序逻辑电路问题，研究的主要内容有

输入信号
输出信号
激励信号
现态和次态的状态信号

2. 时序逻辑电路模型与分类

2.1 时序电路的模型

时序逻辑电路由组合逻辑电路和存储电路组成，其结构可以抽象为下图。

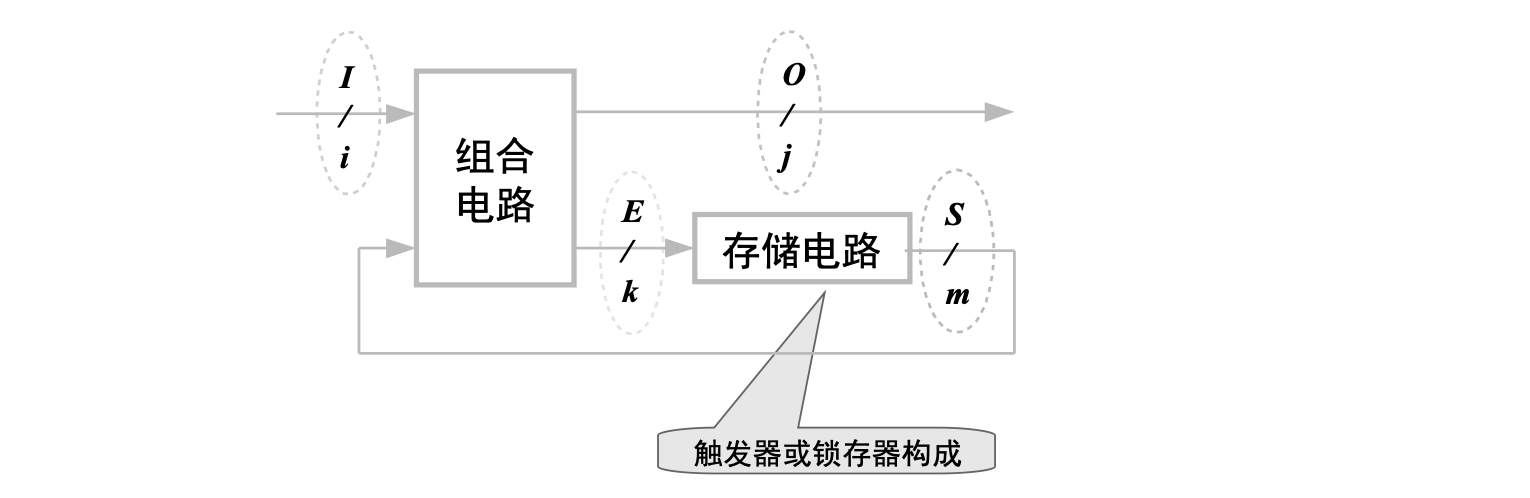
时序逻辑电路共有四组信号，分别是

输入信号：
输出信号：
激励信号：
状态信号：

其中，激励信号本质上是存储电路的输入信号，而状态信号则是存储电路的输出信号。由这些信号可以得到三组方程组，分别是

输出方程组：
激励方程组：
状态方程组：

由这三组方程组，就可以研究在特定状态和输入下，时序逻辑电路的次态和输出。

2.2 异步时序电路与同步时序电路

在时序逻辑电路中，可以根据时钟信号脉冲分为异步时序电路与同步时序逻辑电路

同步时序逻辑电路：构成存储电路的触发器在统一的时钟脉冲信号作用下，各触发器状态在同一时刻进行更新
异步时序逻辑电路：构成存储电路的触发器或锁存器没有统一的时钟脉冲信号，各触发器的状态更新也不是同时发生的。

异步时序逻辑电路又分为脉冲异步时序电路（触发器组成），电平异步时序电路（锁存器组成）

2.3 米利型电路和穆尔型电路

米利型电路

输出信号是输入信号变变量及触发器状态的函数的时序逻辑电路称为「米利型电路」（Mealy），其拓扑结构可以表示为

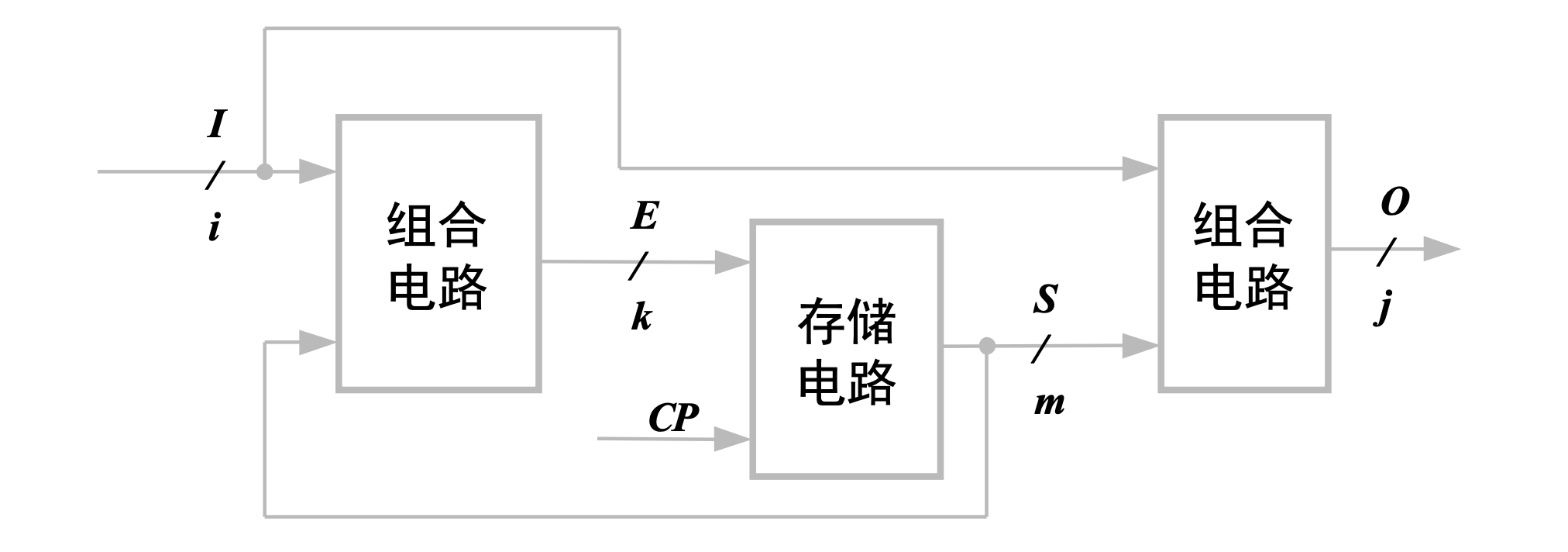
其输出方程组可以表示为：

米利型电路的输入信号与存储电路中的时钟信号是不同步的，因此米利型电路是一个典型的异步电路。

对于米利型电路而言，如果输入信号受到干扰产生毛刺，则干扰可能传递到输出信号端，从而导致干扰传递的现象。因此，米利型电路是一种抗干扰能力较差的电路

穆尔型电路

输出信号仅取决于各触发器的状态的时序逻辑电路称为「穆尔型电路」（Moore），其拓扑结构可以表示为

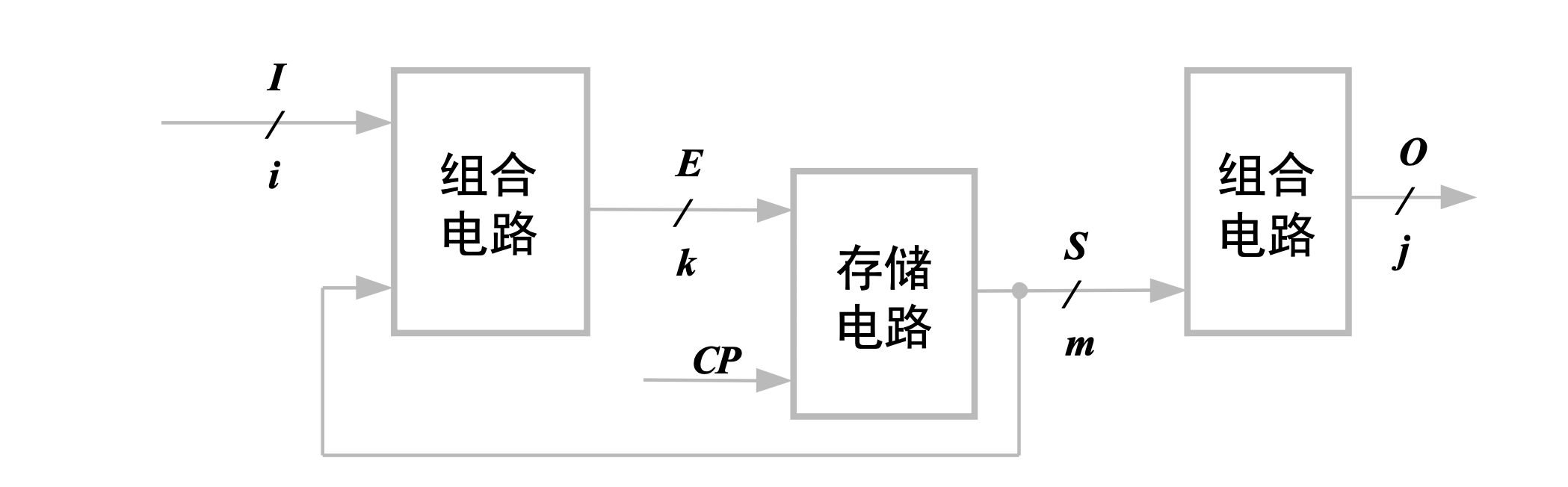
其输出方程组可以表示为：

2.4 电路的状态

电路的现态：各个存储单元都处在稳定的当前现态的组合状态
电路的次态：各个存储单元都转移至稳定的未来次态的组合状态
电路的状态：是触发器或锁存器状态的组合
电路的状态转移关系可被描述为有限状态机，即

$个触发锁存器的电路有个状态$

例如，则电路具有个状态

3. 时序电路功能的表达

之前学过的组合逻辑关系的表达方法有

输出函数表达式
真值表
卡诺图

对于时序逻辑电路而言，不仅要考虑输出端随输入端的变化，还要考虑各个状态之间的转化关系，因此时序逻辑的表达方式比组合逻辑要复杂得多有：

方程组
- 输出方程组
- 激励方程组
- 状态方程组
状态表
状态图
时序图

二、同步时序逻辑电路

1. 分析同步时序电路的步骤

1.1 代数法

了解电路组成

有几个输入端和输出端？电路是米利型电路还是穆尔型电路？电路中存在几个触发器，分别是什么类型的触发器？

写出逻辑方程组

对应每个输出变量导出输出方程，组成输出方程组

传递给各个触发器的激励信号如何表示？

电路的状态是怎么变化的？将各激励信号表达式代入相应触发器的特性方程，得到状态方程组

得到状态表、状态图及时序图

状态表

所谓状态表，就是已知现态，在不同的输入下，表现出怎样的次态和输出，如一个有四状态的米利型状态表，在不同的输入下，呈现不同的输出和次态

现态	次态

状态图

根据状态表，就可以画出各个状态之间互相转换的状态图

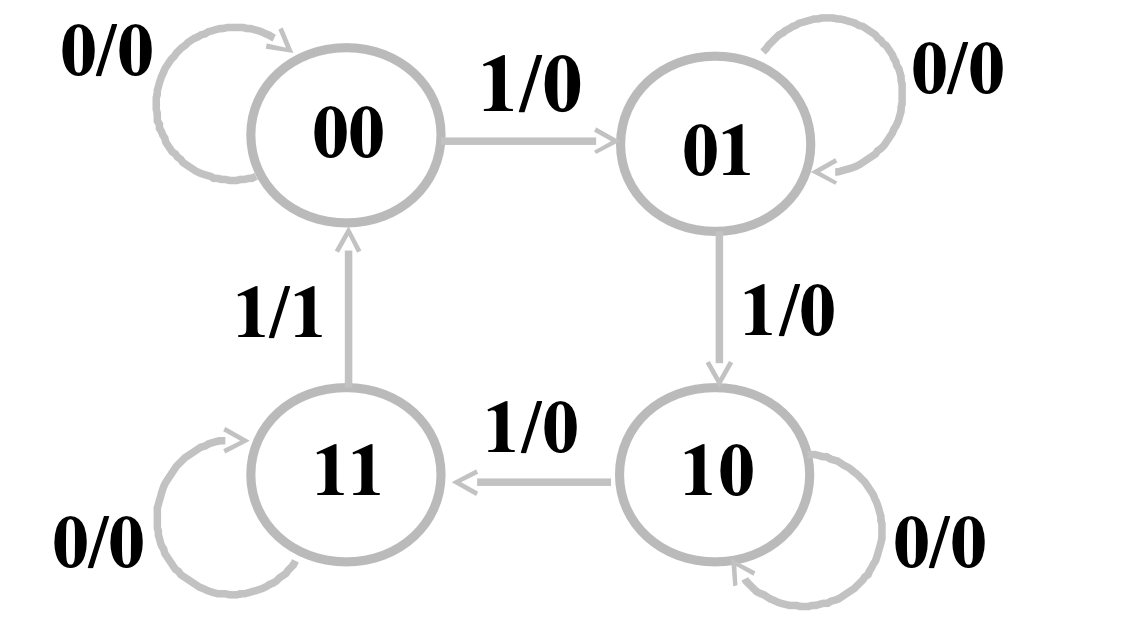
时序图

有了状态图，就可以给出在一个典型输入下，各个量的时序变化关系

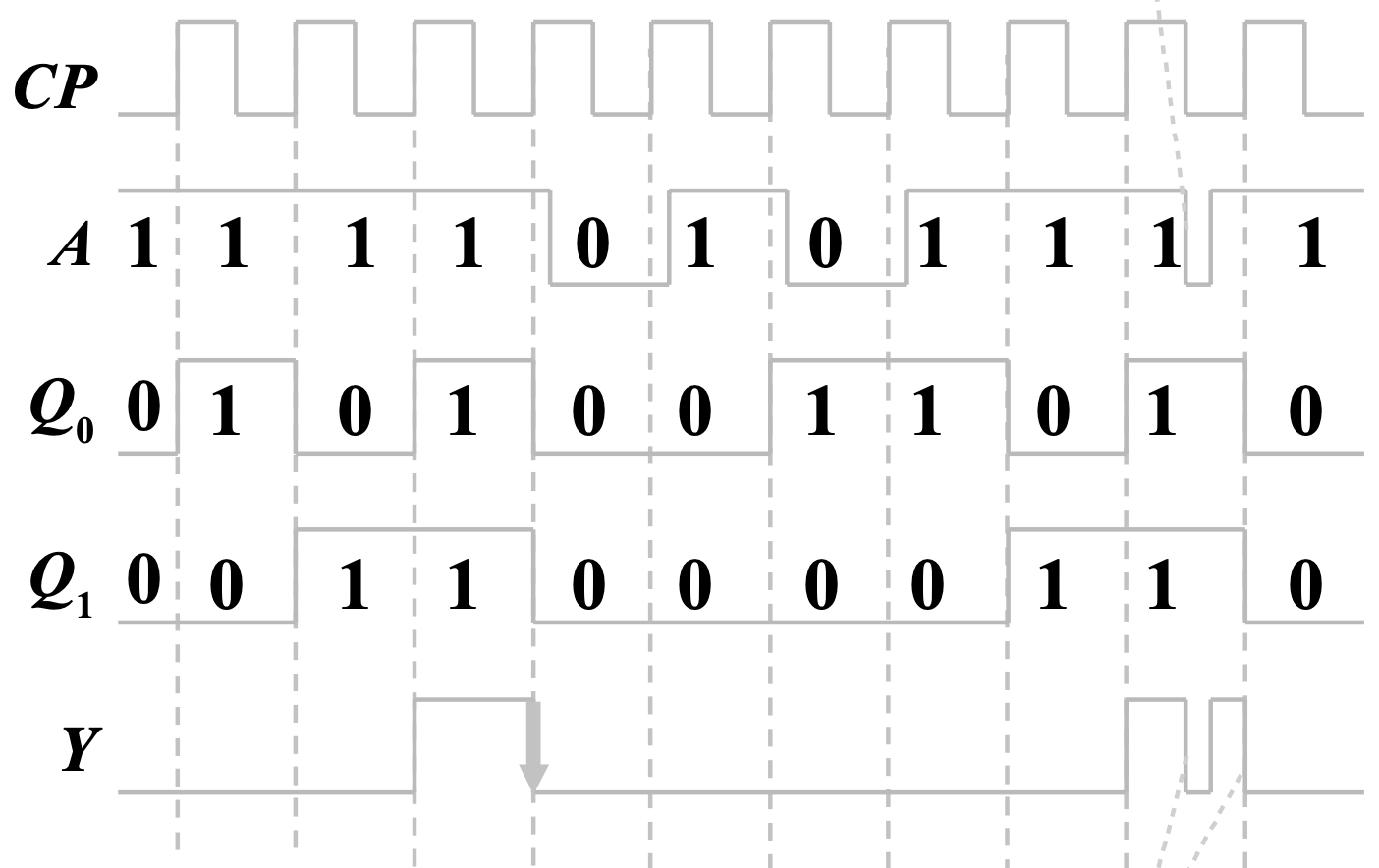
文字表述

最后，用文字表述电路的逻辑功能

1.2 表格法

大多数步骤相同，不同的是根据激励方程组，直接列出电路的「次态真值表」，如

输入	现态	激励函数	次态

较为复杂，因此在考试中不建议使用

2. 同步时序逻辑电路分析举例

已知电路如图所示，分析其电路功能

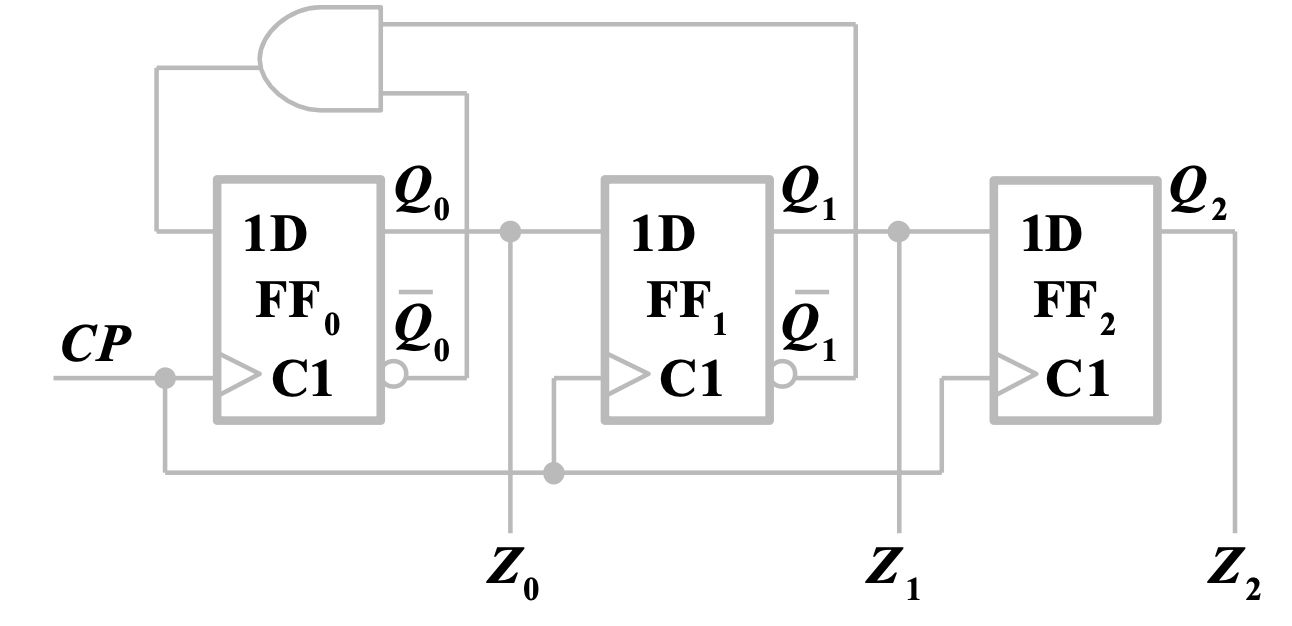
2.1 了解电路组成

电路由 3 个 D 触发器组成了穆尔型同步时序电路，上升沿触发。无输入信号，状态即输出。

2.2 写出各方程式

对于输出方程组

激励方程组

状态方程

由于是穆尔型，因此可以列出与输入无关的状态表


0	0	0	0	0	1
0	0	1	0	1	0
0	1	0	1	0	0
0	1	1	1	1	0
1	0	0	0	0	1
1	0	1	0	1	0
1	1	0	1	0	0
1	1	1	1	1	0

则其状态图为

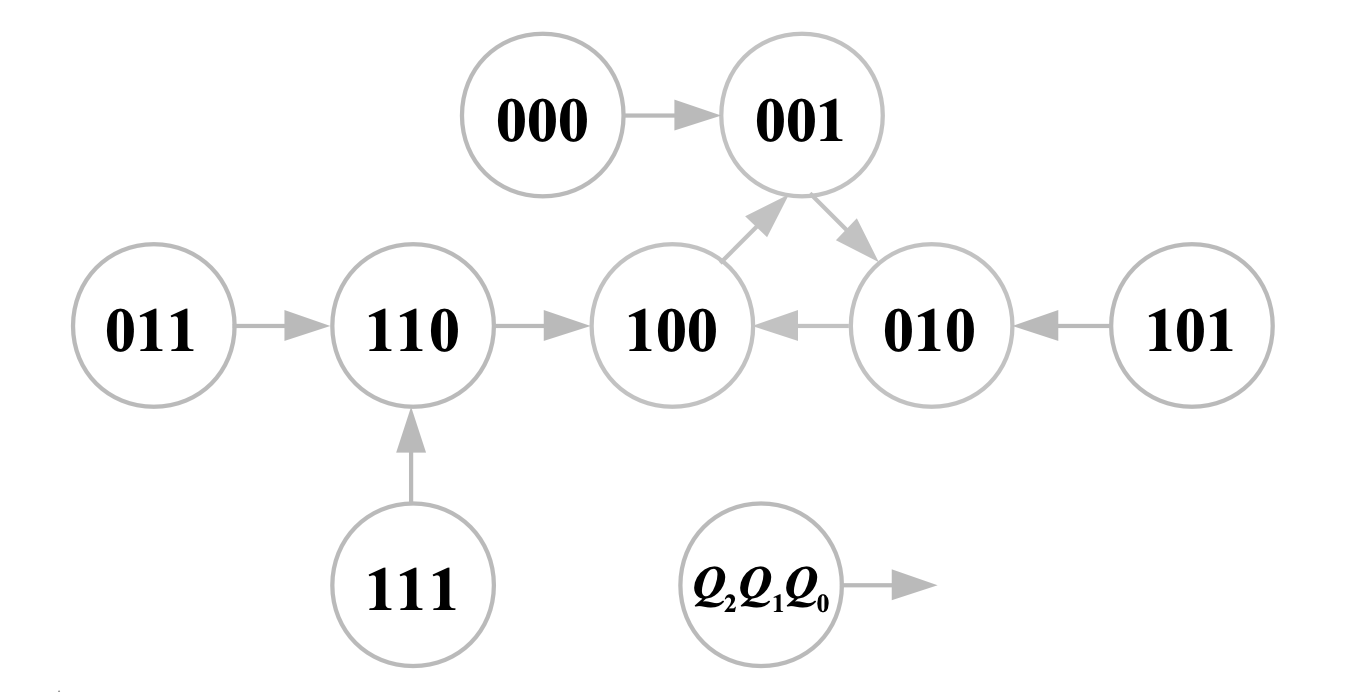
发现此电路无论从何状态开始，最终总会进入 "001,100,010" 这个循环

若一个电路在任意初始状态下，经过若干 CP 脉冲之后，总能进入有效序列，那么此电路具有的这种能力称为「自启动能力」。

此题正是一个具有自启动能力的三位循环码计数器，循环周期为，其有效状态为，而其他状态均为无效状态。但在这种状态图的情况下，若电路初始状态为其他五个无效状态，其经过若干 CP 脉冲之后，总能进入有效序列，因此这个计数器是具备自启动能力的。

由于此电路可以把时钟信号分为三个脉冲，因此可以作为脉冲分配器或节拍脉冲产生器

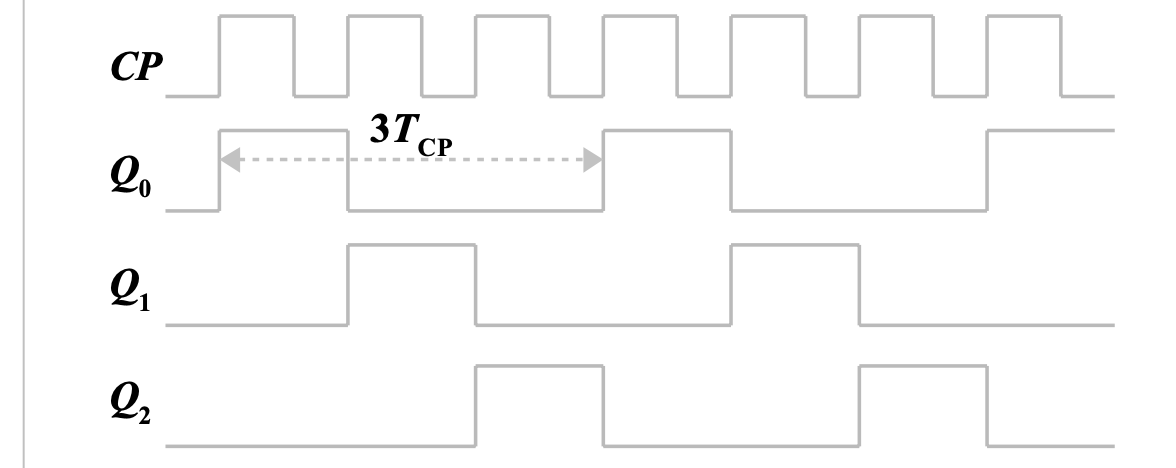
3. 同步时序逻辑电路设计

3.1 设计步骤

同步时序逻辑电路的设计是根据问题需求，设计出响应功能的电路

设计的目标：使用尽可能少触发器和逻辑门实现预定逻辑功能

设计的一般步骤

逻辑抽象

确定输入、输出变量，对其进行命名

分析状态关系。首先确定初始状态，然后从初始状态出发考虑在各种输入作用下状态的转移和输出响应，根据需要记忆的信息增加新的状态，只有当某个状态下输入信号作用的结果不能用已有状态表示时，才增加新状态。

形成原始状态表和状态图

首先先建立一个初始状态，根据在各种输出下需要记忆的信息增加新的状态，确定各时刻电路的输出。

然后根据需求，建立各个状态之间转换的「原始状态表」和「状态图」。

注意检查是否存在等价状态，即相同输入时，输出和次态也相同。在状态表中，应删去这些重复的等价状态

状态化简的编码

对涉及的各个状态指定二进制编码，若位二进制状态码，则需要个触发器，工程中常采用格雷码表示相邻状态。

给每种状态分配二进制码后，以二进制码的方式画出状态表

选择触发器类型

选择一个触发器，按照二进制状态图，列出「状态转换真值表」和激励信号，参见「触发器的激励表」

二进制「状态转换真值表」




...	...

根据二进制状态转换真值表，画出卡诺图，注意无关项要用 x 标识出来，比如对于 8421 十进制加计数器，共有十个有效状态，需要四位二进制码表示，则其关于的卡诺图可以表示为

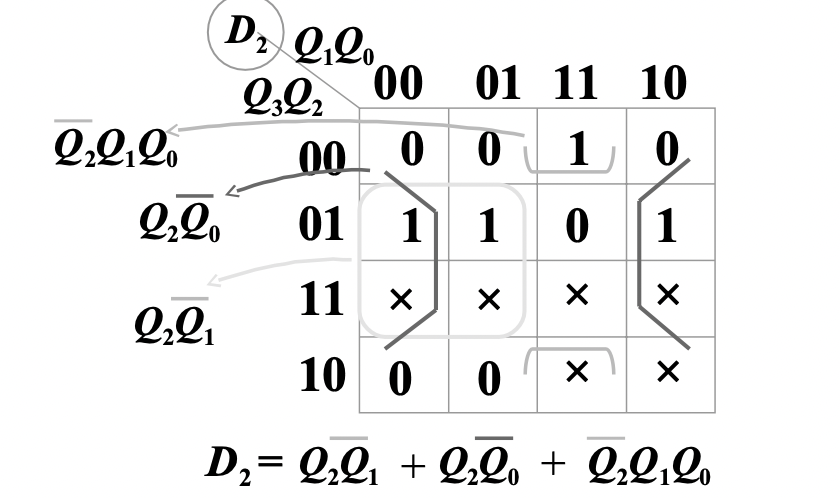
通过卡诺图化简即可得到的表达式。

求激励函数和输出函数最简表达式

根据卡诺图得到每个触发器需要的激励信号，即激励函数。如上图，根据卡诺图得到了

同时也需要从中得到输出方程，如

检查自启动能力

有几个有效状态，有几个无效状态。

对于无效状态而言，在通电后能否进入有效状态？将无效状态作为现态，代入电路的状态方程组，求出次态。若还没有进入有效状态，再以新的状态作现态求次态，以此类推，看最终是否进入有效状态

有时候自启动过程可能会产生误输出，需要用与门修改输出方程。

画逻辑电路图

根据激励函数方程组和输出方程组，画出逻辑电路图

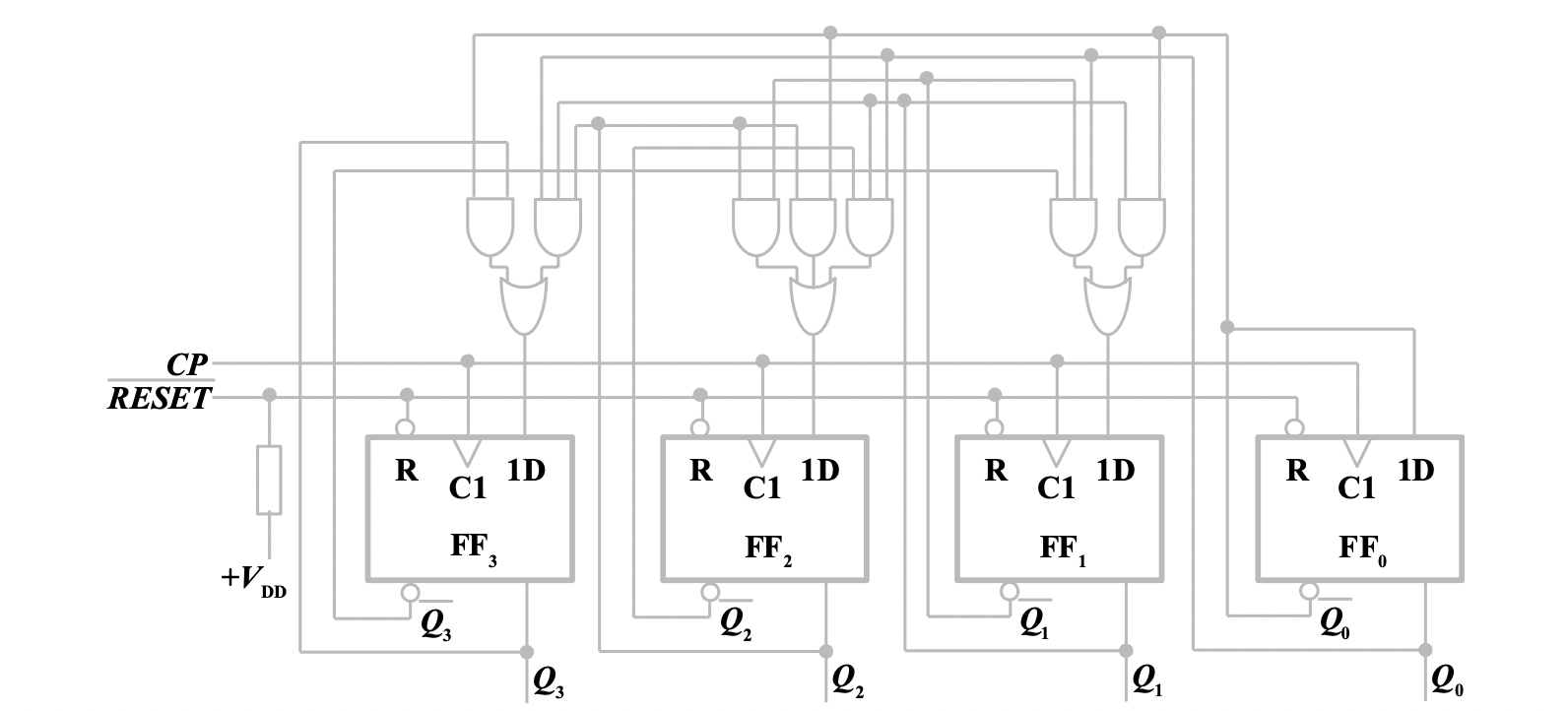
在选择触发器时，尽量选择有异步置零端的触发器，从而可以使用 RESET 电路进行初始置零

存储电路的初始化方法

对于不具有自启动能力的电路，需要设计初始化手段

可利用触发器的异步置 0、置 1 功能，对电路状态进行初始化

触发器的激励表

设计是根据已知，从某现态变至某次态，需求出其对应的激励信号。因此可以用激励表来描述。

激励表的左为现态和次态的转移关系，右栏为其所需的激励信号。比如对于 D 触发器而言，可以画出激励表

	D

三、异步时序逻辑电路

1. 异步时序逻辑电路的分析方法

1.1 异步时序逻辑电路的特点

没有统一的时钟脉冲信号同步
各存储元件状态变化不一定发生在同一时刻

1.2 分析步骤

脉冲异步时序逻辑电路分析步骤与同步时序电路分析基本相同

写出时钟方程

目的：

表示各个触发器何时发生状态变化，从而确定变化的相对先后顺序

如某个有两个触发器的电路

因此，在之后的分析中，第一个触发器是否工作，就需要关注信号，第二个触发器是否工作，就需要关注。注意，这里的等式不表示电平，而是有效边沿。如为上升沿有效，则表示为上升沿时，有效。

写出输出方程和激励方程组

如

了解局部电路的功能，有助于对电路的理解。在对应的触发器被有效沿激活时，根据此激励方程组，触发器状态发生变化

得到次态方程组或列电路次态真值表

从而画出状态表。在画的过程中，先注意第一行为，即外部的时钟有效沿。令初始状态为，则第一行前三列填好了，再来根据时钟方程写出两个触发器的触发信号是否为有效沿，从而写出次态。得到次态后，以此类推即可。

注意，各状态转换项须从输入信号所能触发的首个触发器开始，逐级确定，各状态转换均有一定的时间延迟。

从次态到次态的转换过程中，会存在一段「不稳定时期，在此期间，电路的状态是不确定的，只有全部触发器状态转换完毕后，电路才进入新的「稳定状态」，即电路的次态


1	0	0	1	1	1	1
1	1	1	0	1	1	1
1	1	0	1	1	0	1
1	0	1	0	1	0	0

一共四个状态，实现循环

若存在多个状态，也要把循环之外的状态包括进去

作出状态表、状态图和时序图

确定电路逻辑功能，检查自启动

2. 注意事项

2.1 有效沿的表示

分析状态转换时，必须考虑各触发器的时钟信号作用情况。若为有效边沿，则令，否则。注意！这里的和不表示电平，只表示有效沿！

根据激励信号确定的触发器次态，的触发器保持不变

2.2 逐级确定

各状态转换须从输入信号所能触发的首个触发器开始，逐级确定

2.3 时间延迟

判断状态变化时，需要在脑海里加上一定的延迟。

从现态到次态的转换过程中，会存在一段“不稳定”时期，在此期间，电路的状态是不确定的。只有全部触发器状态转换完毕后，电路才进入新的“稳定”状态，即电路的次态

3. 例题

3.1 例1

分析如图所示异步电路

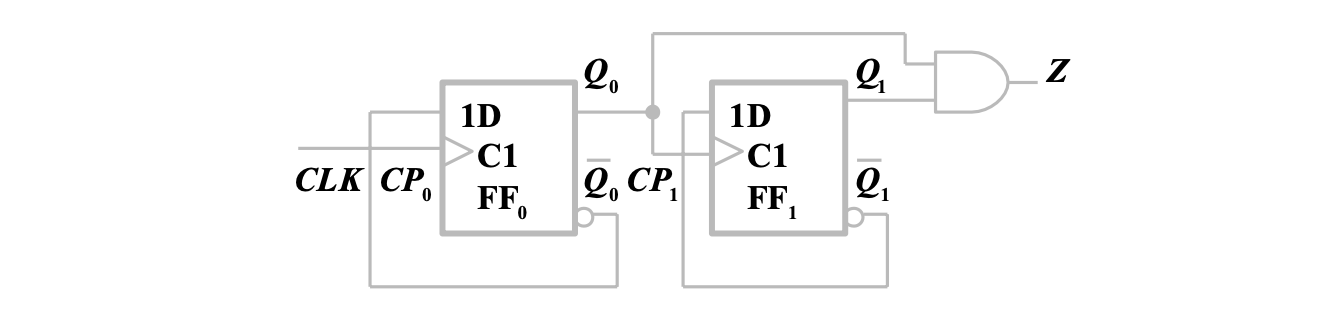
列方程式

时钟方程

输出方程

激励方程

状态方程

由此作出状态表


1	0	0	1	1	1	1
1	1	1	0	1	1	1
1	1	0	1	1	0	1
1	0	1	0	1	0	0

从而得到状态图

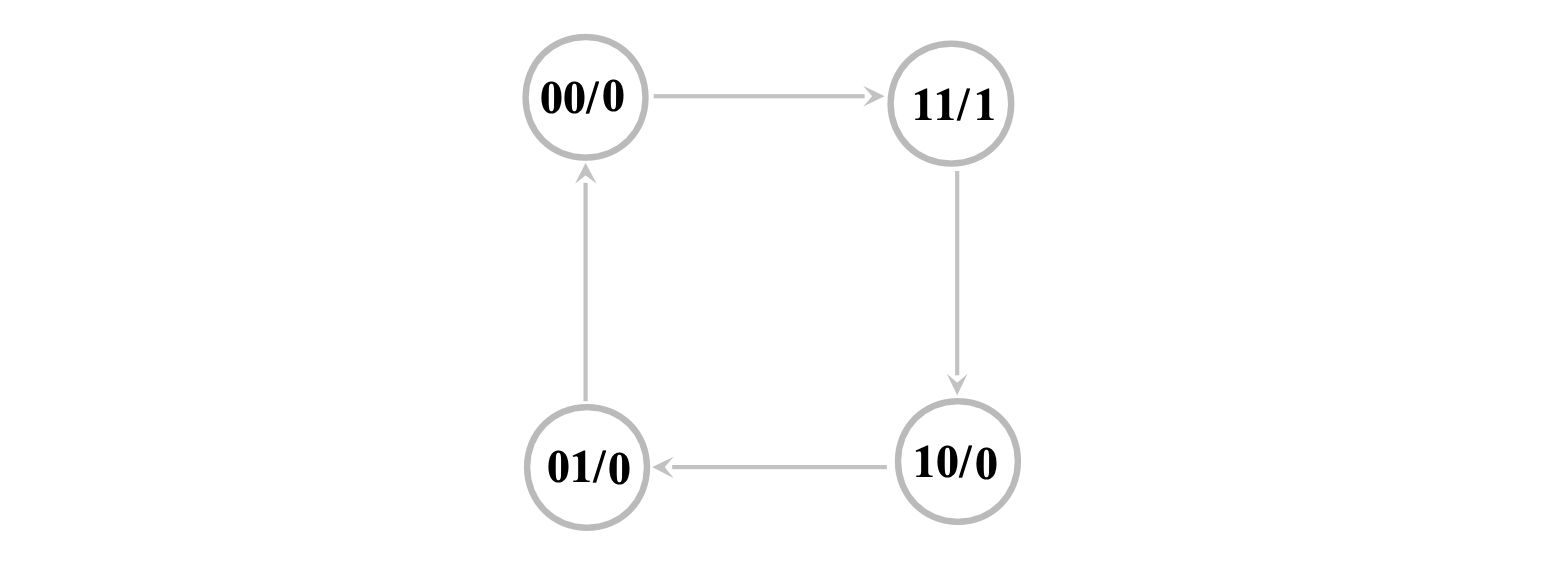
时序图

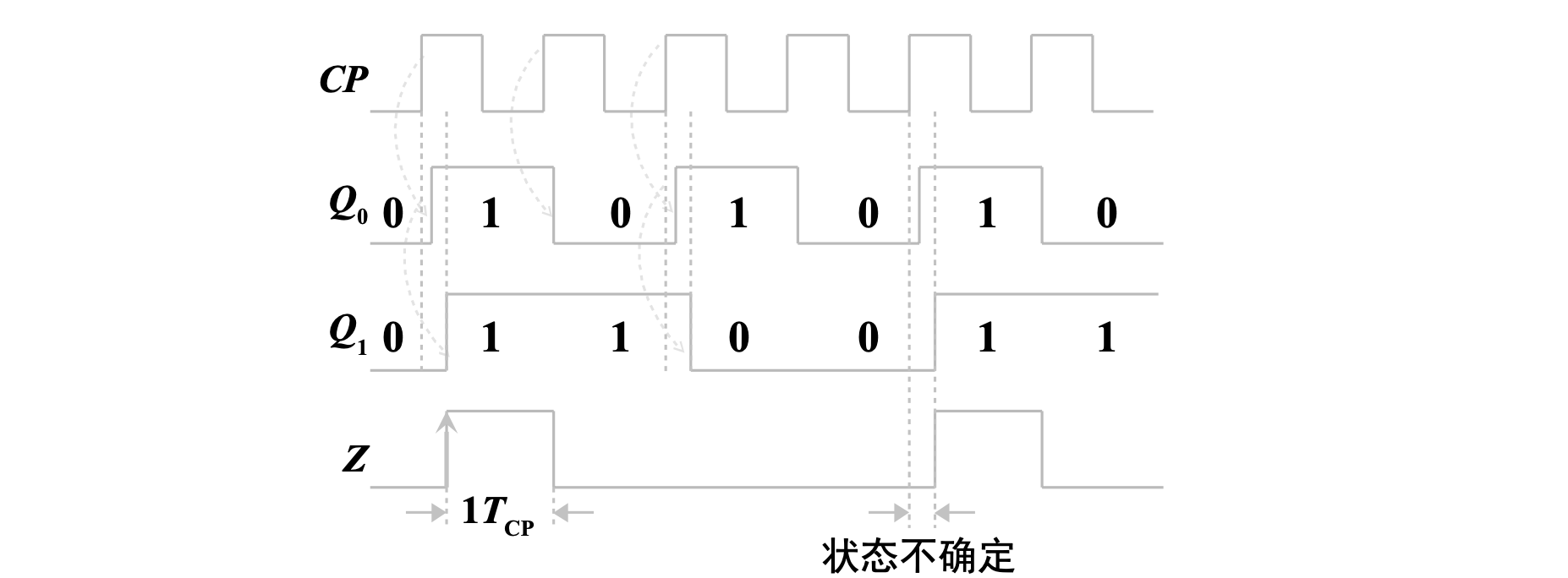
逻辑功能

是异步二进制减计数器，信号的上升沿为借位标志。电路也有序列信号发生器的功能

四、若干典型时序逻辑集成电路

1. 寄存器

1.1 寄存器

由触发器组成的用于存储代码或数据的逻辑部件叫做「寄存器」，位寄存器包含个触发器，可存储位二进制代码

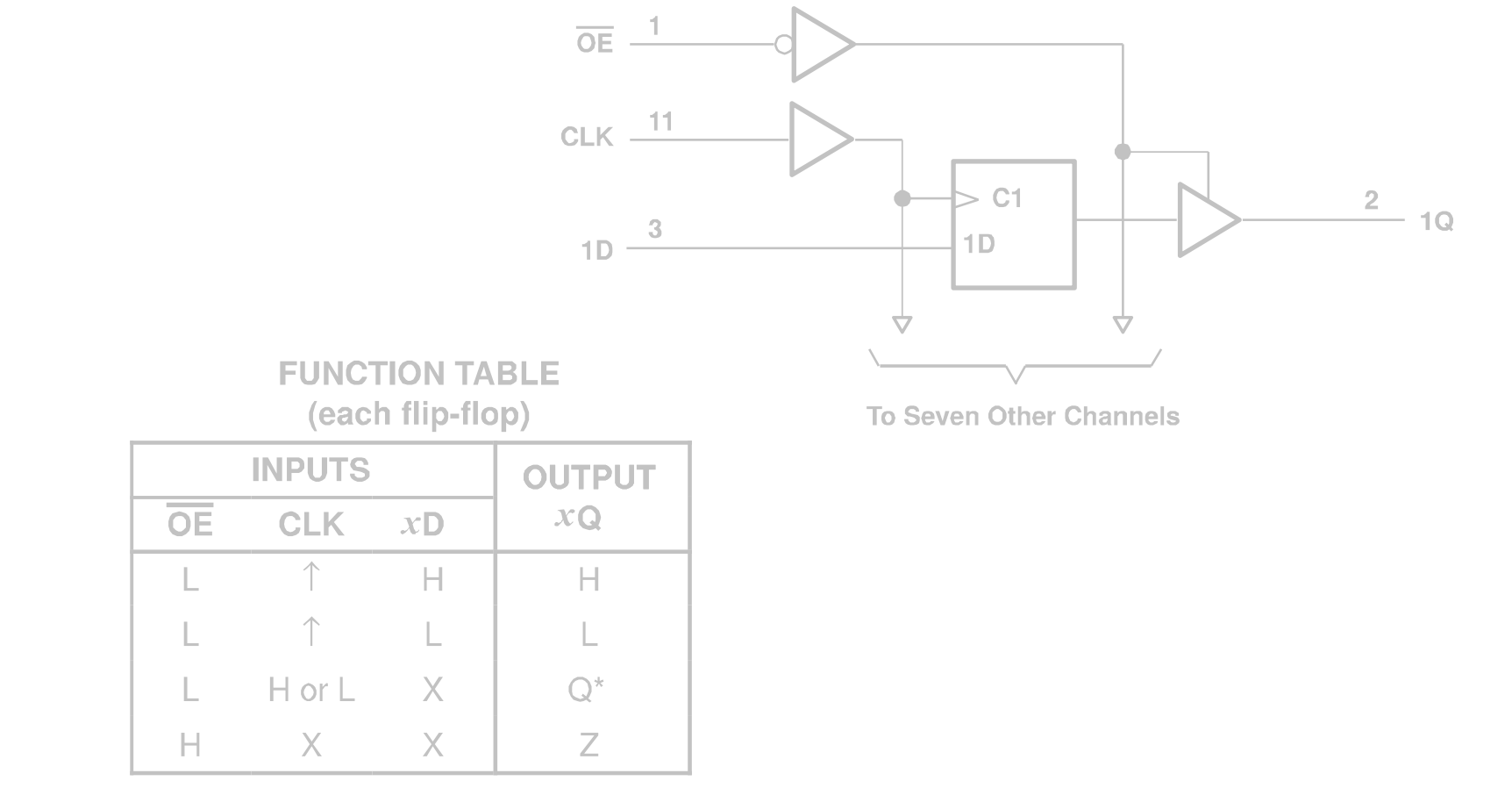
如: 74HC374 是由个触发器构成的位 CMOS 寄存器，与锁存器 74HC373 具有类似的逻辑功能，只是脉冲边沿和电平敏感的差别

一般寄存器比锁存器具有更好的同步性能和抗干扰性能

1.2 移位寄存器

既能寄存数码，又能在时钟脉冲的作用下使数码向高位或向低位移动的逻辑功能部件叫做「移位寄存器」

国家标准规定：逻辑图中低位到高位排列是从左至右，因此

右移：数据从低到高;
左移：数据从高到低

按照移动方式，移位寄存器可以分为：

单向移位寄存器
- 左移位寄存器
- 右移位寄存器
双向移位寄存器

基本移位寄存器

基本移位寄存器一种单向移位寄存器，具有一个「串行数据输入端」，若干个「并行数据输出端」和一个串行数据输出端。在每个时钟有效沿到来时，各触发器中的数据「右移」一位，串行数据输入端的信号被存储进入最低位，而最高位的信号从串行数据输出端输出。

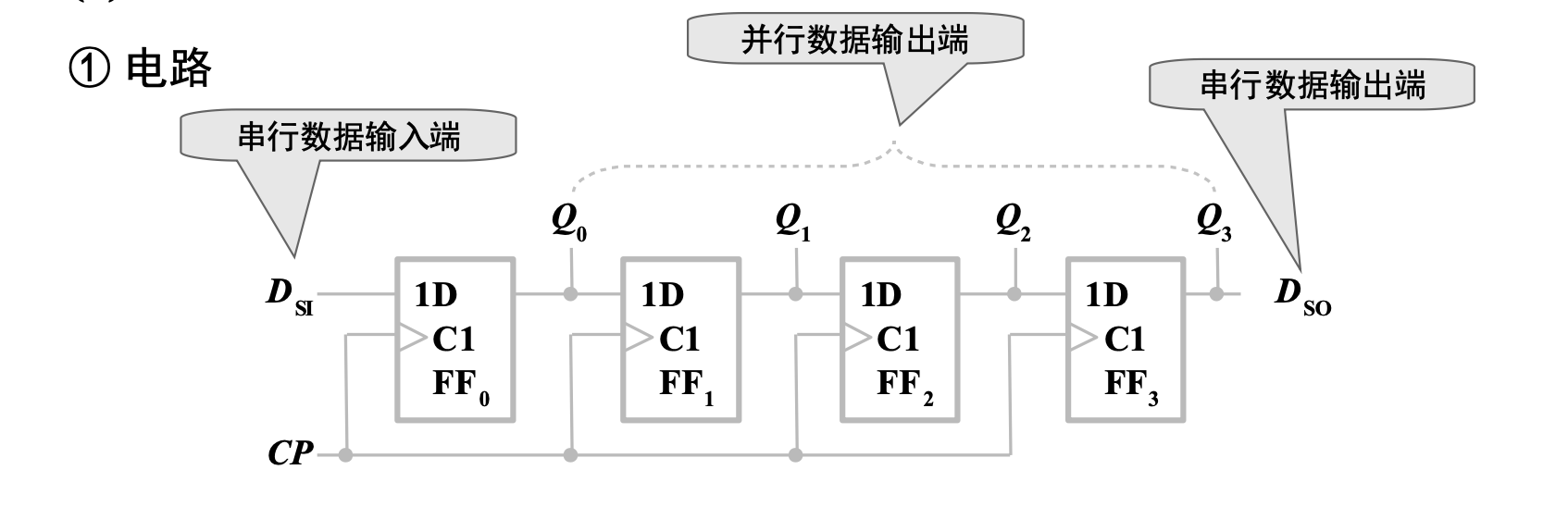
激励方程：

状态方程：

多功能双向移位寄存器

数据既可以右移，也可以左移，多功能指还具有其他功能，如并行输入、输出等。其状态图可以表示为

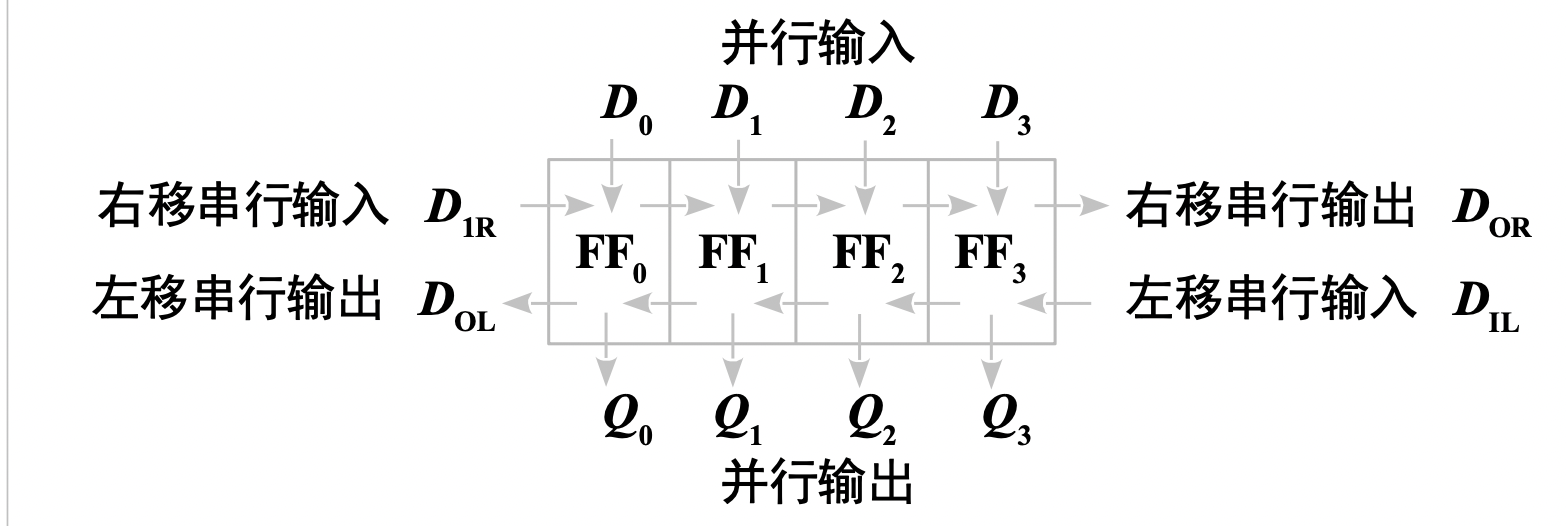
实现多功能双向移位寄存器的一种方法，可以通过数据选择器和多个 D 触发器组成

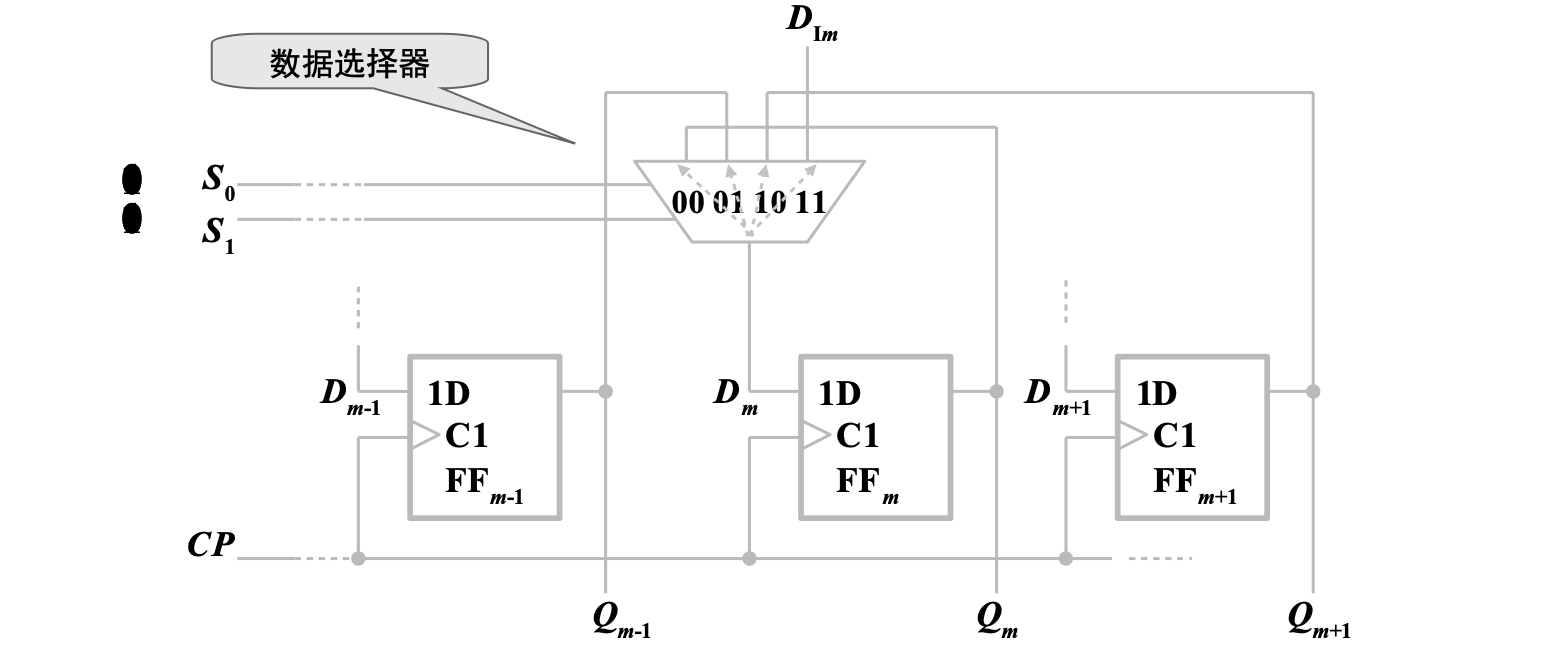
当时，此时，，此时寄存器始终保存当前状态
当时，此时 $，$ Qm^{n+1}=Q{m-1}$，此时寄存器为右移状态
当时，此时，，此时寄存器为左移状态
当时，此时，，此时寄存器为并行输入状态

典型集成电路 74HC194

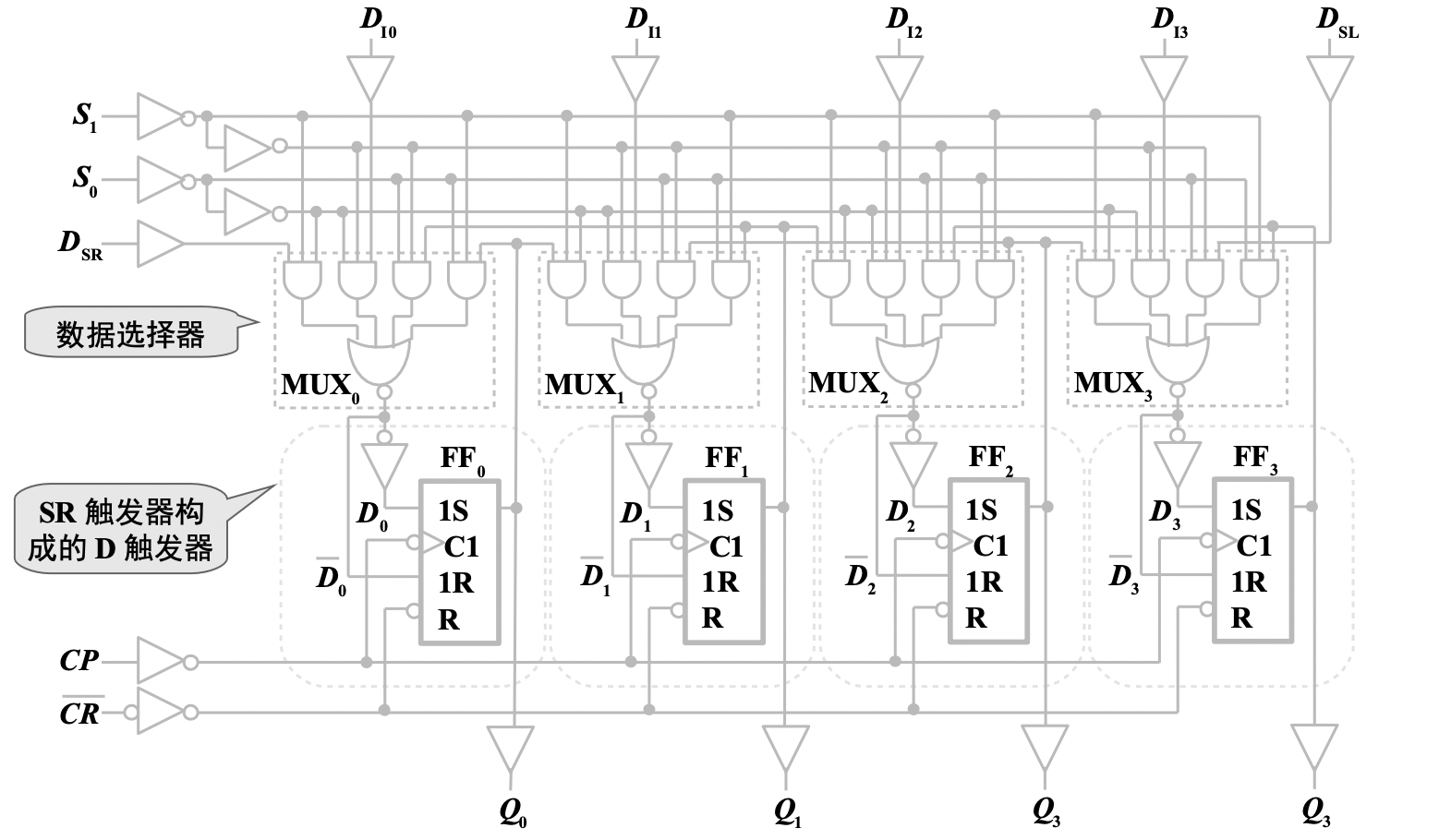
2. 计数器

计数器的功能就是对脉冲进行计数，常用作定时、分频、产生节拍脉冲和脉冲序列及进行数学运算等。

计数功能：当时钟有效沿到来时，计数器状态码递增或递减
分频功能：状态码各位输出脉冲信号的频率是时钟脉冲的分频信号。N 进制计数器最高位是时钟脉冲的 n 分频信号

在脉冲的作用下，计数器的状态按序转移，每个状态由计数器的状态码来表示，这样的状态码叫做计数器的「数」，而计数器的有效状态数叫做计数器的「模」

2.1 二进制计数器

异步二进制计数器

如图是一个最简单的由四个 T' 触发器构成的二进制计数器

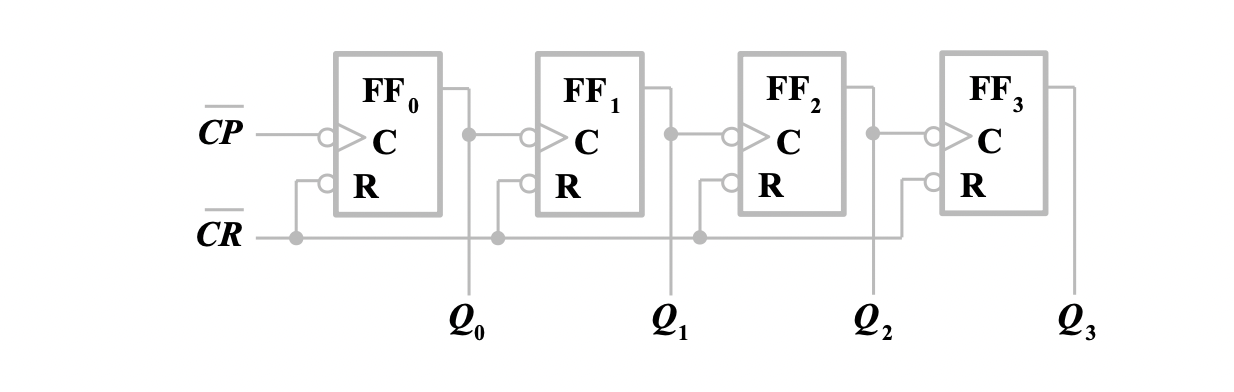
当脉冲下降沿到来时，翻转，若出现下降沿，则翻转，以此类推。则其波形图为

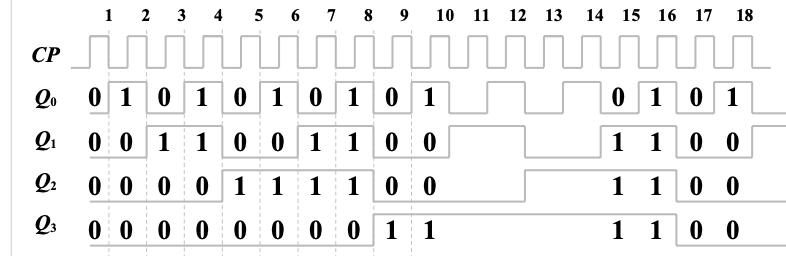
在计数的同时也能实现分频。设时钟频率为

为二分频，
为四分频，
为二分频，
为二分频，

但考虑到各触发器都有的延时，该异步计数器由延迟累计问题，故要求其满足：

因此位数越多，对时钟脉冲频率限制越大，因此更希望使用同步时序逻辑电路的计数器

典型集成电路 74HC393

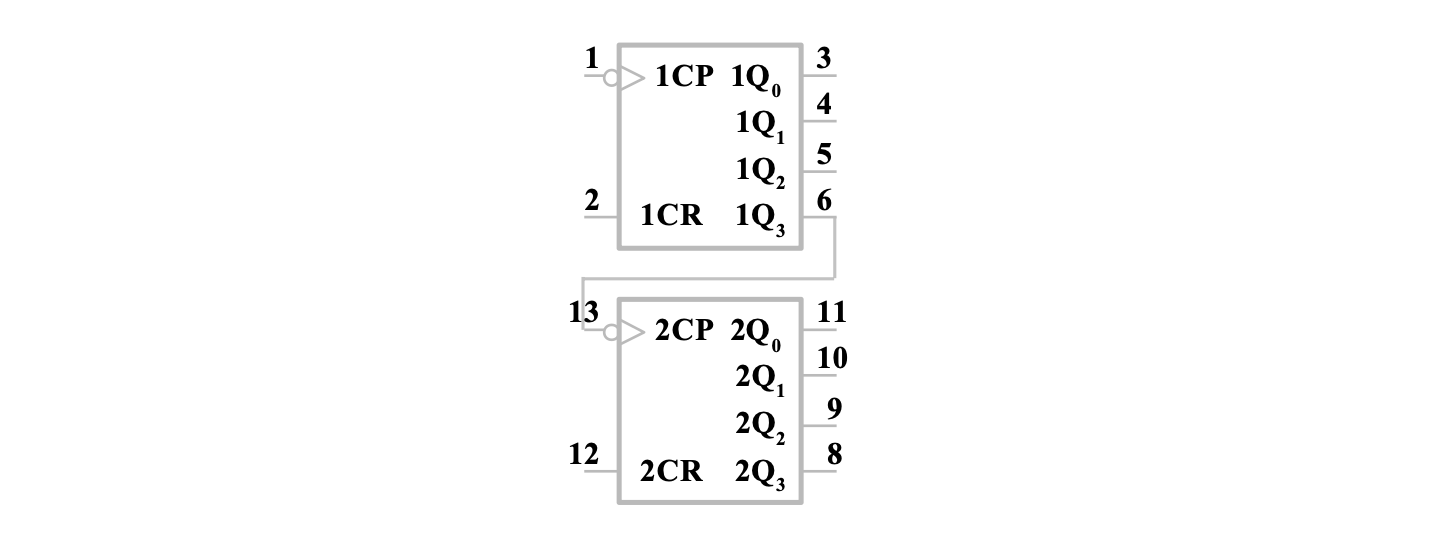
内部集成有两个独立的异步计数器，低位计数器的最高位接在高位计数器的时钟信号端。形成 8 位模 256 的计数器

在 $、$ 下，触发器传输延迟时间为

下降沿出发，具有异步清零端

同步二进制计数器

为了防止延迟的积累，不能通过级联的触发器逐个改变状态的方式来实现进位，而是使用逻辑门「提前」实现运算。对于任何一位来说，当且仅当前面所有数位为时才能反转，即，因此本质上，需要对前面的数位作与运算。由此得到电路

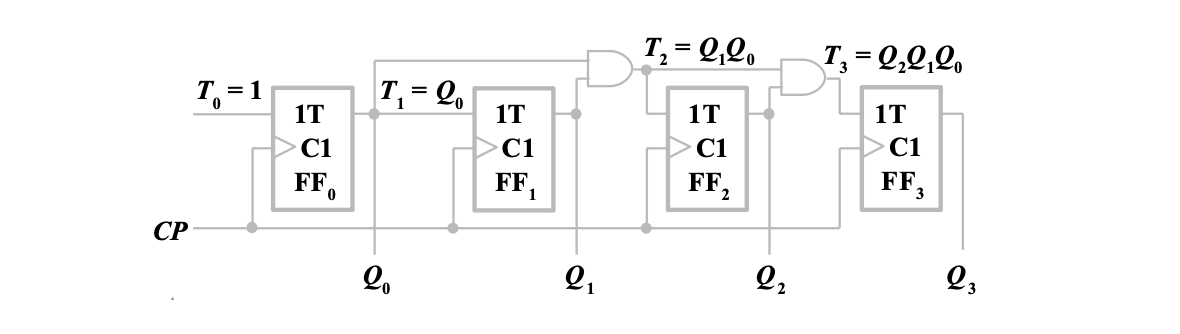
从而实现延迟只停留在本位，并不会因为位数的增加而产生延迟累积

典型集成电路 74LVC161

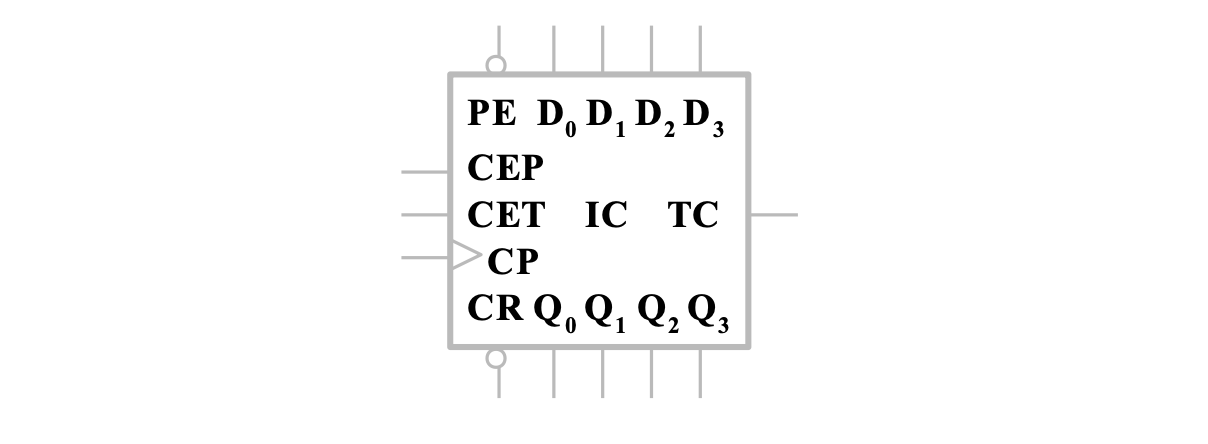
时钟脉冲输入：
异步清零输入：
并行使能输入：
并行同步置数输入：
计数和进位使能输入：和，二者同时为时可计数
计数器状态输出：
进位标志：，当且时，，其下降沿表示进位

其逻辑功能表为

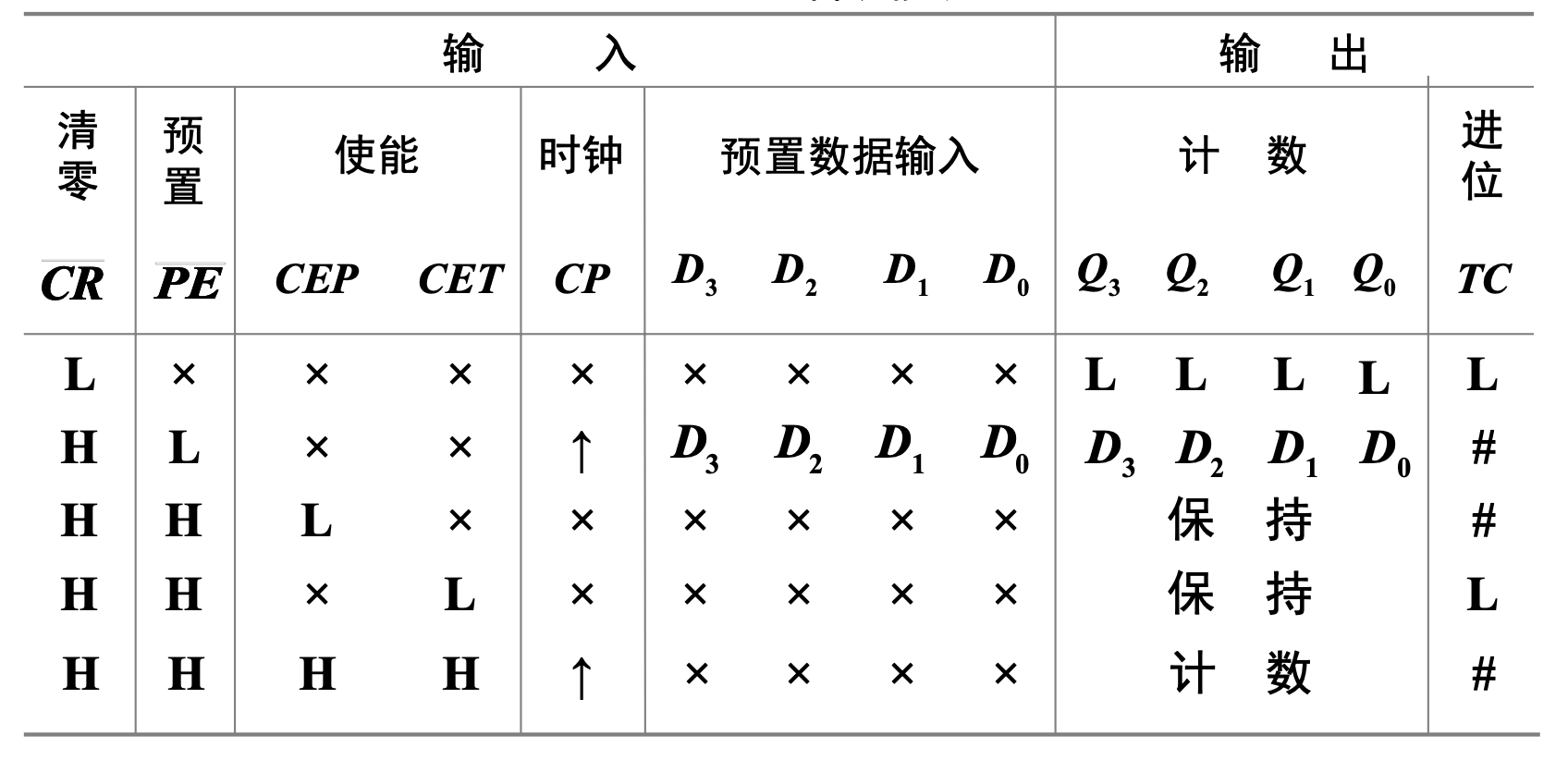
电路结构为

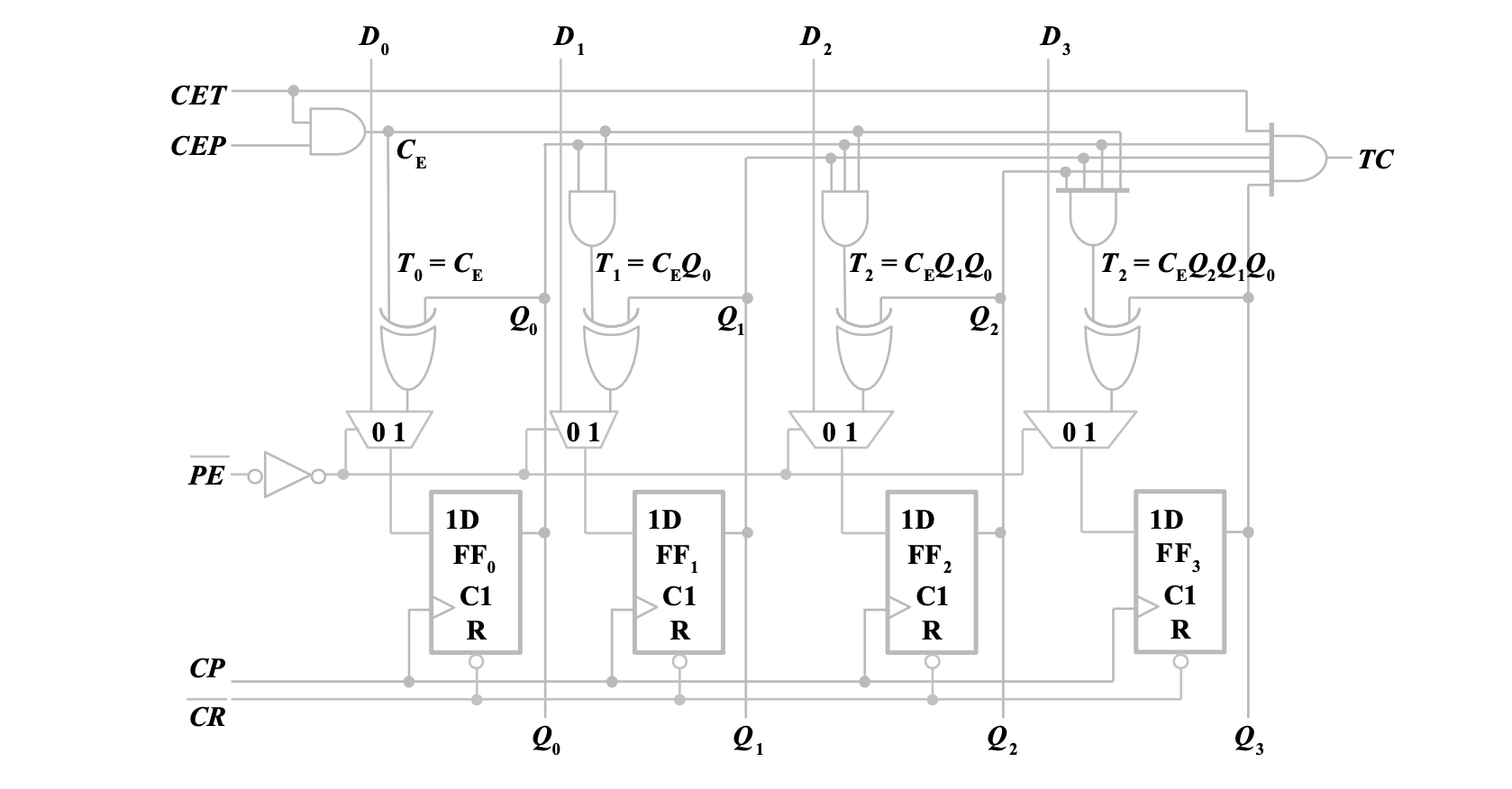
使用集成计数器构成任意进制计数器

可用模计数器实现模计数器，若，则需多片模计数器

反馈清零法

适用于具有清零输入端的计数器

异步清零：对计数器的目标尾状态之后的状态译码，产生异步清零信号，是计数器立即被异步清零
同步清零：对计数器的目标状态译码，产生同步清零信号，等下一时钟有效沿到来时，使计数器同步清零

异步清零在达到尾状态时，可能产生瞬间的毛刺。为此，尽量使用同步置数段实现置零。如用 74LVC61 构成九进制加计数器，在 1001 状态被瞬间清零，采用的是异步清零。

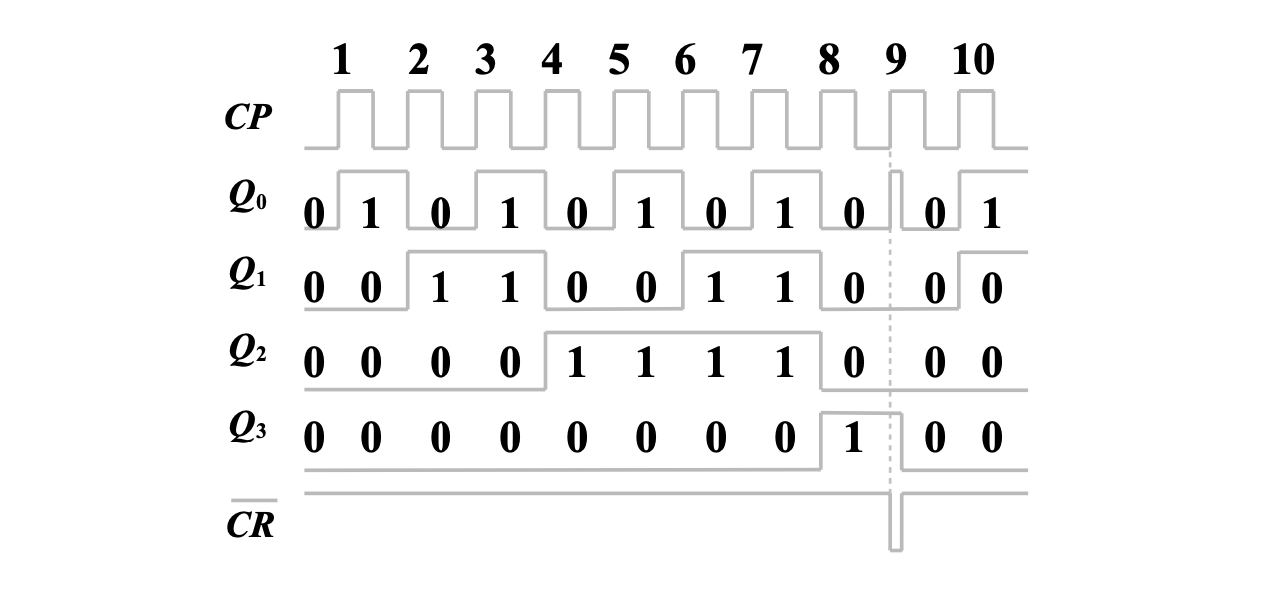
反馈置数法

适用于具有同步置数输入端的进程计数器

对计数器的目标尾状态译码，同步置数使能信号，等下一时钟有效沿到来时，是计数器状态置为预置数。

2.2 环形计数器

基本环形计数器

将最后一位输出接在第一位输入端，就构成了基本环形计数器，如下图

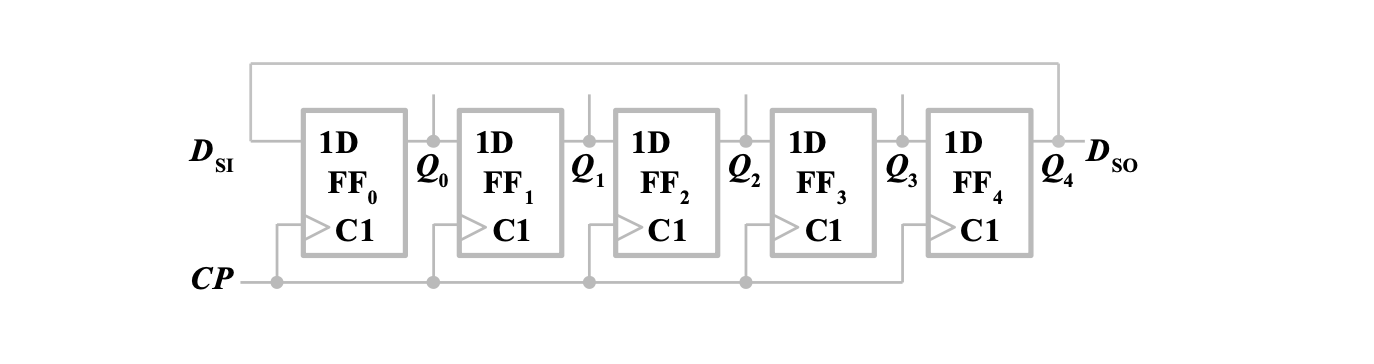
设初始状态为，则随着上升沿到来，状态变为

扭环形计数器

基本环形计数器使用了 5 个触发器，只有 5 个状态，触发器利用率较低，若将移位寄存器反相输出与输入相连，形成一个类似八字形的扭环结构，则构成扭环形计数器

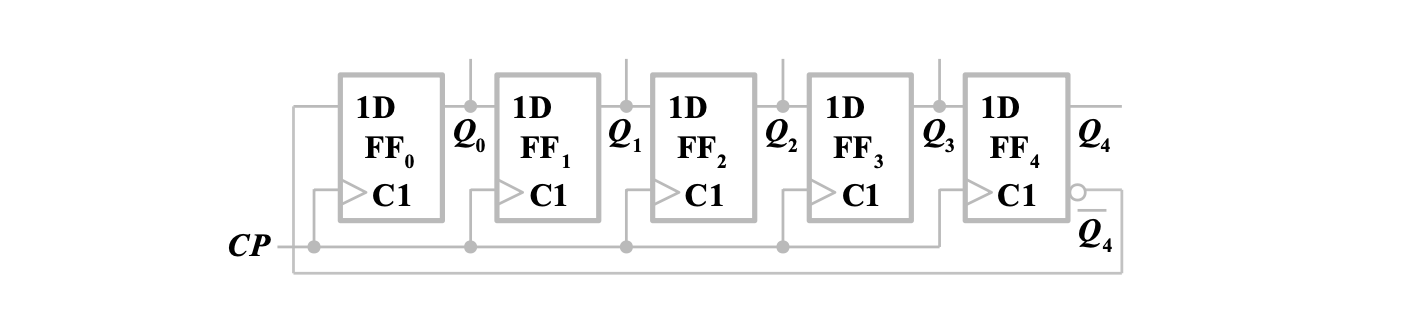
上图的扭环形计数器由 5 个触发器组成，有 10 个有效状态，状态图如下

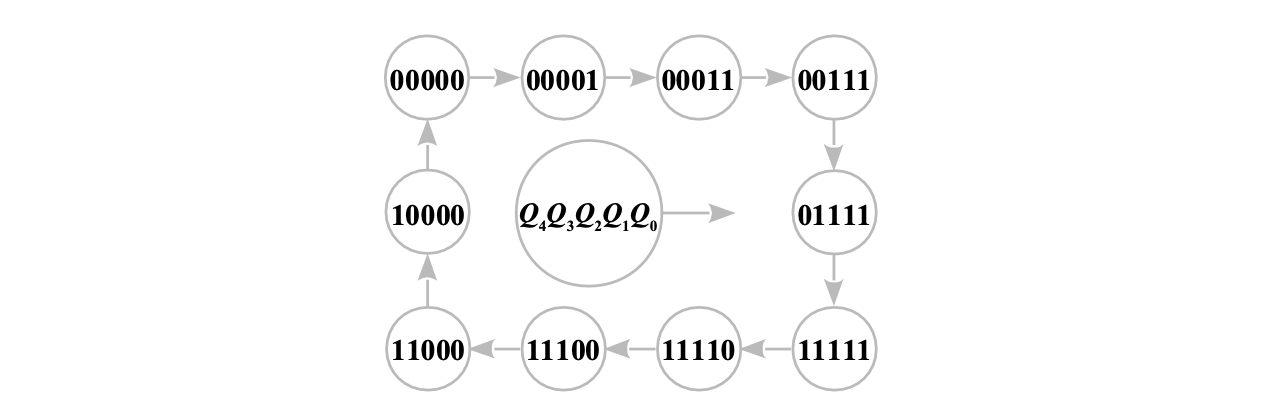
只有10个有效状态，需要设计对应电路，使其能自启动

需要对其进行编码，选择关键位，即与其他状态不同的两位来写出译码输出表达式

五、时序逻辑可编程逻辑器件

1. 常用可编程逻辑器件

1.1 通用阵列逻辑（GAL）

在 PLA 和 PAL 基础上发展起来的增强型期间

其内部逻辑直接继承了组合 PLD 的与或结构

每个输出端都设置了 OLMC

1.2 复杂可编程逻辑器件（CPLD）

集成了多个逻辑快，每个逻辑夸就相当于一个 GAL 期间

逻辑快之间可通过共享可编程开关阵列组成互联资源，实现新交换，也可与周围的 IO 模块相连，实现芯片外部交换信息

1.3 现场可编程门阵列（FPGA）

是目前设计高度复杂时序系统的首选方案之一
结构与 GAL、CPLD 有很大差别
芯片内部主要由不同功能的可编程逻辑模块组成
靠纵横交错的分布式可编程互联线连接起来，可构成极其复杂的逻辑电路

2. GAL 的结构

根据门阵列结构，现有 GAL 分为两大类:

与门阵列可编程，或门阵列固定，类似 PAL 基本相似，如: GAL16V8
与门阵列和或门阵列都可编程，如: GAL39V18 等

GAL 的输出端增设了可编程的输出逻辑宏单元（OLMC），编程可将 OLMC 设置为不同的工作状态，产生组合、时序逻辑电路输出

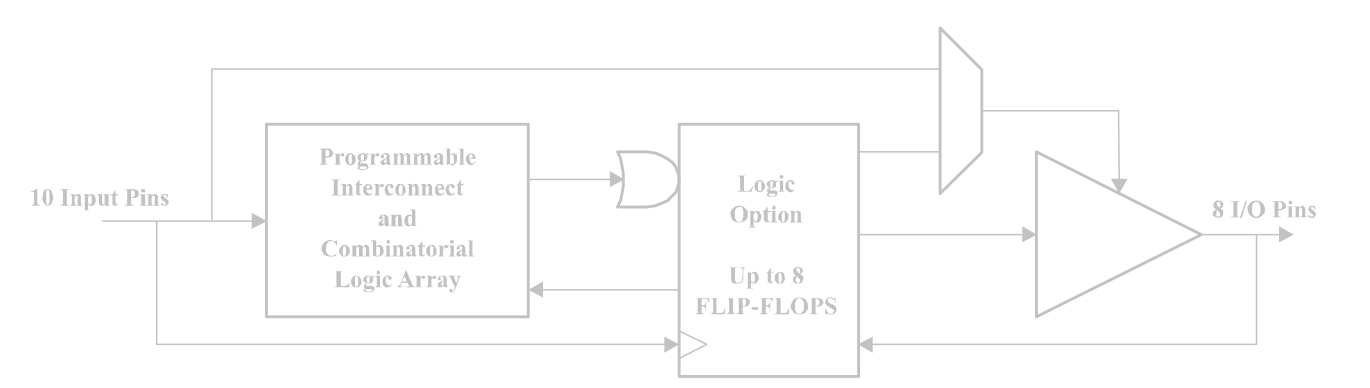
六、用 Verilog 描述时序逻辑电路

1. 触发器的 Verilog 建模

D 触发器的异步与同步置 0 行为

异步置零：

module A_DFF(output reg Q, input D, input CP, input _RD);
    always @(posedge CP, negedge _RD)
        Q <= (~_RD) ? 1'b0 : D;
endmodule

同步置零

module S_DFF(output reg Q, input D, input CP, input _RD);
    always @(posedge CP)
        Q <=(~_RD) ? 1'b0 : D;
endmodule

2. 计数器的 Verilog 建模

设计一个具有异步置零功能的四位加减计数器

module _4bit_counter(output reg [3:0] Q, input CP, _CLR, Mod)
    always @(posedge CP, negedge _CLR)
        if (~_CLR) Q <= 4'b0000;
        else Q <= (Mod ? Q + 1 : Q - 1)
endmodule

变模计数器

module var_cnt(output reg [3:0] Q,input CP, _CLR, EN,S1, S0); 
    always @(posedge CP, negedge _CLR)
    if (~_CLR) Q <= 4'd0; 
    else if (EN)
    begin
        case ({S1, S0}) 
            2'b00: Q <= (Q <4‘d5) ? Q + 1'd1 : 4'd0;
            2'b01: Q <= (Q <4‘d7) ? Q + 1'd1 : 4'd0; 
            2'b10: Q <= (Q <4‘d9) ? Q + 1'd1 : 4'd0;
            2'b11: Q <= (Q <4‘d14) ? Q + 1'd1 : 4'd0;
        endcase
    end
    else Q <= Q;
endmodule

通过模式控制信号，可以改变计数器的模

		模
0	0	6 进制
0	1	8 进制
1	0	10 进制
1	1	15 进制

穆尔型状态图，可采用 1 个 always 语句块实现

module moore_machine(output reg [1:0] Q, input A, CP, _CR);
    always @(posedge CP, negedge _CR) begin