逻辑运算
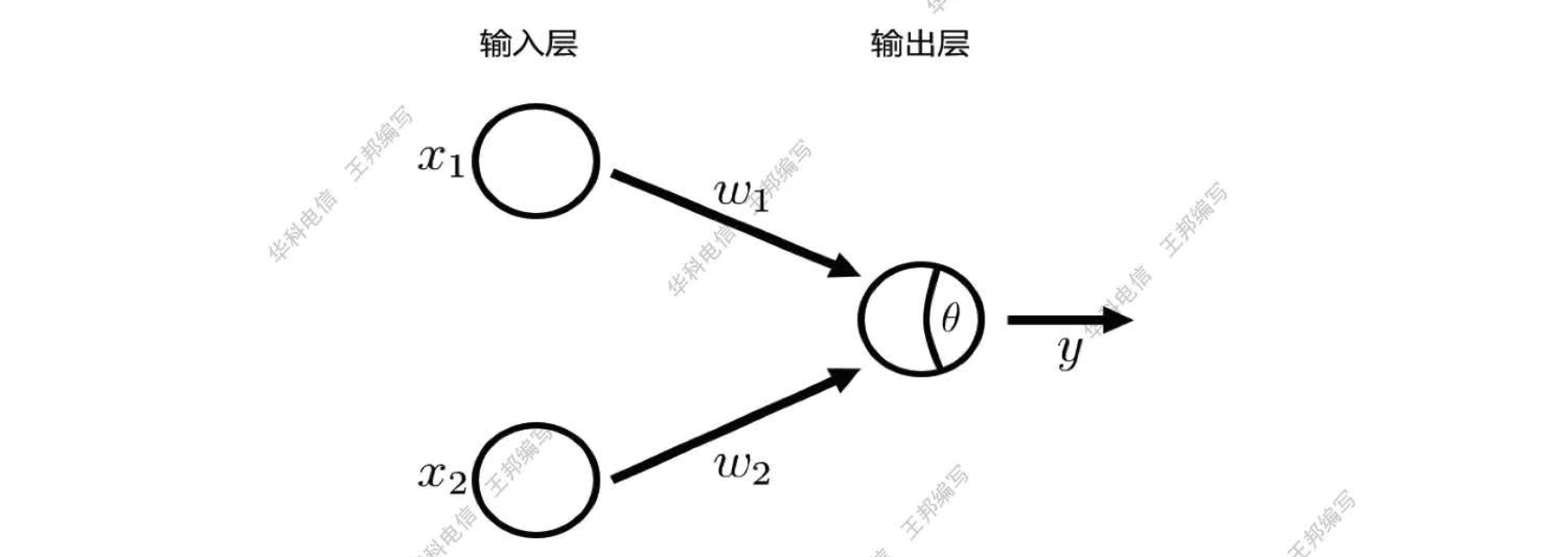
感知机学习
给定数据集,权值
学习方法如下:对训练样例
- 若预测正确,即
- 若预测错误,则根据错误程度对
可以证明,若两类模式是线性可分的,即存在一个线性超平面能将他们分开,则感知机的学习过程一定会「收敛」(Converge)而求得适当的权重向量
要解决非线性可分,则需要考虑使用多层功能神经元构建多层神经网络

给定数据集,权值
学习方法如下:对训练样例
可以证明,若两类模式是线性可分的,即存在一个线性超平面能将他们分开,则感知机的学习过程一定会「收敛」(Converge)而求得适当的权重向量
要解决非线性可分,则需要考虑使用多层功能神经元构建多层神经网络