恒定电场

电子（载流子）在电场的作用下发生宏观运动，形成「真实电流」，这样形成的电流又有传导电流和运流电流之分，其中：

传导电流：在导电媒质（导体，半导体或漏电介质）中，电荷（载流子）的流动所形成
运流电流：真空中或气体中电荷（载流子）流动所形成

可见，传导电流和运流电流都是由真实存在的电荷（正电荷或负电荷，统称载流子）运动产生的。除了这两种电流外，还有一种电流称之为「位移电流」，它对应于变化的电场，并不表示任何带电质点的运动，它遵从于 Maxwell 方程组。不随时间变化的真实电流叫做「恒定电流」，恒定电流产生的电场，称为「恒定电场」

一、真实电流的密度分布

单位时间内流过某横截面的载流子电荷电量定义为「电流强度」，可以表示为

在垂直载流子运动的方向取一个面元，设通过这个面元的电流强度为，则定义「电流密度」的大小为单位时间内流过单位横截面的载流子的电荷电量，其方向规定为正电荷运动的方向。

可见，电流密度是个矢量，单位为安培/米。设某点处载流子的运动速度为，该点处的载流子电荷体密度为，则在单位时间内流过横截面面元的电荷为

写为矢量形式为

此处应特别注意是指载流子的体密度，在金属导体中即是自由电荷的体密度，而不是导体中净电荷的密度。导体中存在恒定电场时，净电荷的密度恒为零，它是单位体积中正电荷与负电荷的代数和。已知后，即可求出流过体积中任意一个曲面的电流强度。

根据上面的定义和推导，我们同样可以得到导体表面上的「电流线密度」（面电流密度）为

面电流密度的单位为：安培/米。上式中，是表面上运动电荷（载流子）的面密度，是其运动速度。对应有关系：

注意：对于线电流，不定义密度函数，而只有线电流强度。这是因为线电流中只有一个个点

二、恒定电场的基本方程

设导体中电流密度为，并任意选定导体中一个由闭合面包围的体积为研究对象。从闭合曲面流出的电流为

它表示单位时间内从体积穿出曲面的电量，即体积内电荷的减少率。根据电荷守恒定律有

记为净电荷的体密度，由于，因此

应用散度定理，化上式左边的闭合面积分为体积分，得

由于是任意的，因此有

上两式分别称为「电流连续性方程」的积分形式和微分形式，它们适用于任何形式的真实电流。对于恒定电流产生的恒定电场，其中的电荷虽然是在运动的，但是各个点的电荷密度却不随时间改变，即

其中为净电荷密度。在下节中还将证明，当均匀导体中存在恒定电场时，有，因此有

对于恒定电场，尽管电荷在运动，但在电场中任一点处电荷的运动速度并不随时间变化，即电荷分布不随时间变化。因此，恒定电场与静止电荷电场（静电场）具有相同的性质，也是保守场，满足环路定理：

对应的微分形式为

从而

可见，恒定电场也可以用电位函数表示。

三、导体中传导电流的性质

1. 导体中的欧姆定律和焦耳定律

导体中传导电流是由于导体中电场对载流子的作用力并使之以动而产生的，而导体中的电场归根结底是由于施加于导体两端的电源产生、并维持导体中的电流和电场持续存在。电源将化学能（或其他形式能量）转化为导体中的电场能。电源的性质可以用「电动势」这一概念进行描述，它表示在电源内部的等效电场对电荷做功：

$电源内$

单位为伏特，在电源内部，的方向为从电源负极指向正极。可见，在恒定电场中，沿穿过电源的一个闭合回路对电场强度积分时，有

$电源内电源外$

$电源内电源内$

可见，在包含电源的情况下，总电场是一个非保守场。但是在电源外部的导体中，电场仍具有保守性。根据金属电子理论和实验结果可知，导体中任一点处的电流密度与该点处的电场强度成正比，即

上式称为「导体的本构关系」，或称为欧姆定律的微分形式。其中，为导体的「电导率」，它是导体电阻率的倒数。另一方面，导体中的功率密度可以表示为为：

上式分别为「焦耳定律」的积分形式和微分形式。即：电场力在单位时间内对单位体积中的载流子所做的功可以表示为

将欧姆定律的微分形式代入，并认为是常数，则

即

因此。上式表示，当导体中电荷分布达到稳定时，即电源对导体的充电已达到稳定，已在导体中建立了恒定电场，对于均为常数的导体，均匀导体内任一一点处的净电荷密度为零。在对导体充电的过程中，即导体中电荷分布还未达到稳定，还处于暂态过程中时，将导体本构关系式代入电流连续性方程，并利用，和，得

即

解得

其中称为「弛豫时间」。可见，在充电过衡中，导体中的净电荷密度随时间按指数规律减小到零，达到稳态时，导体内部不存在净电荷，净电荷都分布到导体表面上了。由于恒定电场为保守场，即

将其带入（均匀导体中），得

所以，恒定电场中任一点满足 Laplace 方程

2. 导体边界条件

在本节中重点探讨恒定电场中，导体表面或导体分界面处的边界条件。如图，在导体的接触面，取面元，以及，对此闭合柱面应用电流连续性方程的积分形式得

或

即导体分界面上，电流密度的法向分量连续。在分界上取微小闭合环路，如图

线元平行分界面的切向，且。应用恒定电场中的环路定理得

或

即导体分界面上，电场强度的切向分量连续。用电位表示法向/切向边界条件为

3. 例题

平行板电容器中的恒定电场，极板间填充漏电介质

注意以下几点：

平行电容器中漏电流垂直于极板，即只有法向分量
应用的边界条件
导电媒质分界面上的自由电荷是净电荷，可由高斯定律求得：

四、恒定电场的静电比拟

比较恒定电场与静电场的基本关系式，可知下述参量具有一一对偶的关系：

恒定电场	静电场

所以，对于某一恒定电场的边值问题，如果对应结构的静电场边值问题时已经有解的，则恒定电场的解便可以直接写出，只需将上述各参量进行对应替换即可。称这种方法为「静电比拟法」。所以，许多恒定电场问题都可以化为静电场的问题来解决，反之亦然。

例如，在充满均匀介质的静电场中，有下面两个导体

两导体间的电容为

而由高斯定理，得

另外，因此

而在恒定电场中，求在电导率为的均匀导电媒质中的两个电极之间的电导为

其中，为电极 1 经过导电媒质流向电极 2 的电流，其值为

另外，，因此

可见符合对偶关系。

例题

有一个半径为的导体球，其球心为两种导电介质的分界面上，分界面可视为无限大平面。求：

该球与无穷远点的电阻
当在该球面上加有电压时，介质所消耗的功率

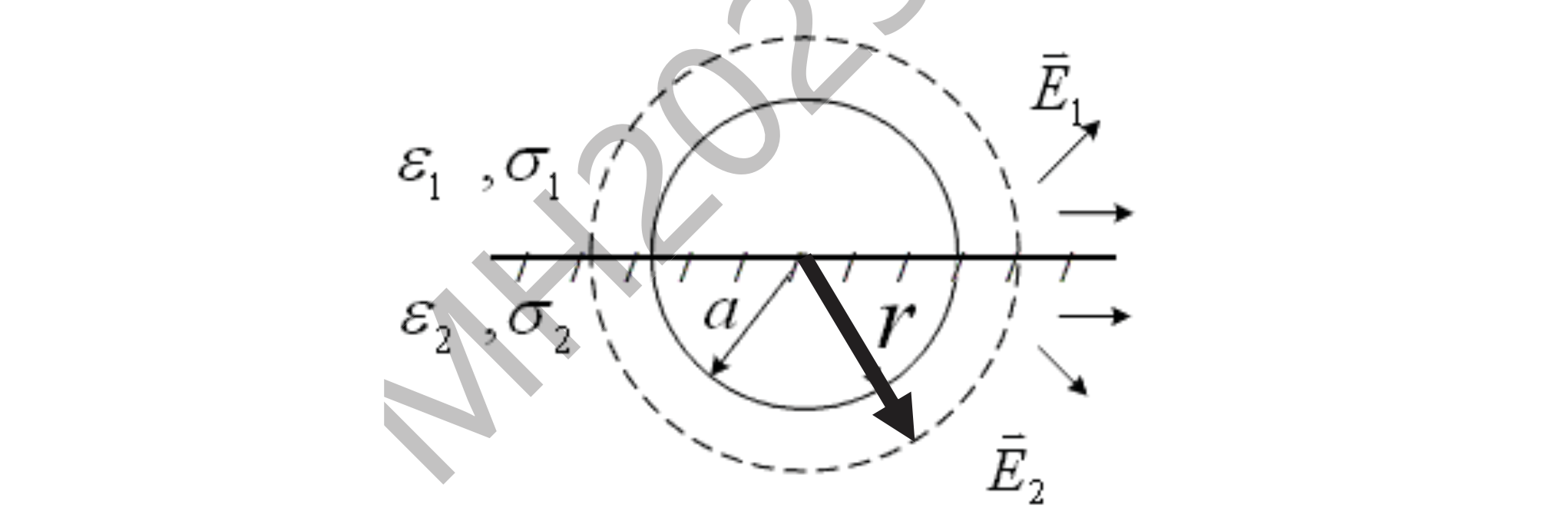
第一题

用静电比拟法，设导体球带电量为，在两种介质中的静电场强为，且均沿径向，则由高斯定理

且根据边界条件有，所以

球至无穷远处的电压为

因此

由静电比拟法得，所以

第二题

当球上加有电压时，由球流走的总电流

而

且均沿径向，且根据边界条件有，所以

因此由焦耳定律得

漏电介质所消耗的总功率为