归纳偏好

在机器学习的模型评估中，如果仅有训练样本，无法断定模型哪一个更好。但对于一个具体的学习算法而言，其必须要产生一个模型。此时，学习算法的「偏好」就会起关键的作用。

机器学习算法在学习过程中对某种类型假设的偏好，称之为「归纳偏好」（Inductive BIas），或简称为「偏好」

任何一个有效的机器学习算法必有其归纳偏好，否则它将被假设空间中看似在训练集上“等效”的假设所迷惑，而无法产生确定的学习结果。可以想象，如果没有偏好，我们的学习算法产生的模型每次在进行预测时随机抽选训练集上的等效假设，那么对这个新瓜，学得模型时而告诉我们它是好的、时而告诉我们它是不好的，这样的学习结果显然没有意义。

归纳偏好可看作学习算法自身在一个可能很庞大的假设空间中对假设进行选择的「价值观」。有没有一般性原则来引导算法确立“正确”的偏好呢？

「奥卡姆剃刀原则」（Occam's razor）：若有多个假设与观察一致，则选最简单的一个

注意，奥卡姆剃刀并非唯一可行的原则。同时也需要注意到，奥卡姆剃刀本身存在不同的诠释，使用奥卡姆剃刀原则并不平凡。

归纳偏好对应了学习算法本身所作出的关于“什么模型更好”的假设。但在具体的现实问题中，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多数直接决定了算法能否取得好的性能。

归纳偏好与具体的问题有关。比如两种学习算法产生了光滑的曲线 和复杂的曲线 。如果基于奥卡姆剃刀原则，假设平滑曲线具有某种“描述简单性”，则我们采用曲线 作为学习的模型

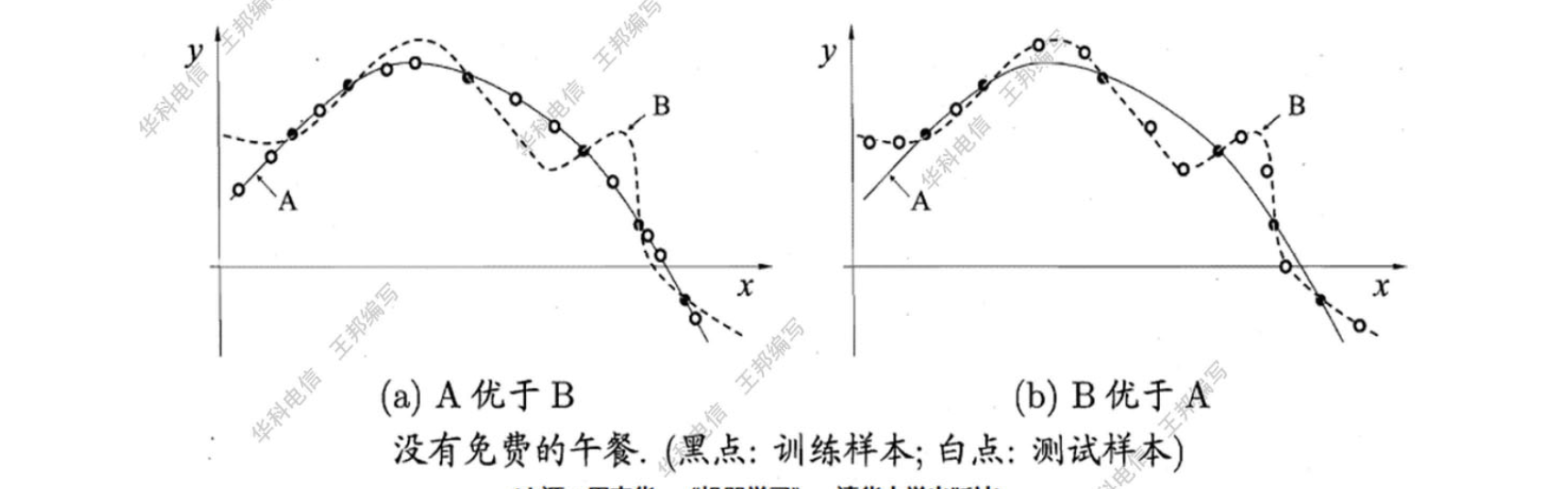
在图 （a）中，我们发现曲线 A 与训练集外的样本更一致，其泛化能力强于曲线 B。但是，在图 (b) 中，我们却发现曲线 与训练集外的样本更一致，其泛化能力强于曲线

注意到两张图中是两个不同的问题，他们的训练集和测试集是不一样的。因此，脱离开问题本身讨论算法性能是没有意义的。

假设样本空间 和假设空间 为离散空间。令 代表算法 基于训练数据产生假设 的概率，令 代表希望学习的到的真实目标函数。则「训练集外误差」定义为

其中 为指示函数，若 为真取值 1，否则取值 0。考虑二分类问题，且真实目标函数可以是任何函数 ，函数空间为 。则对所有可能的 按均匀分布对误差求和，有

（证明略）上式表明，总误差与具体的学习算法无关！对于任意的两个学习算法，都有 ，即两个学习算法的期望性能相同，这对应了天下没有免费的午餐定理

NFL 定理有一个重要前提：所有”问题“出现的机会相同、或所有问题同等重要。但实际情况不是这样，很多时候，我们只关注自己正在试图解决的问题，希望为它找到一个解决方案，至于这个解决方案在别的问题、甚至相似问题上是否为好方案，我们并不关心。NFL 定理最重要的寓意在于指出脱离具体问题，空泛地谈论“什么学习算法更好“毫无意义。要谈论算法的相对优劣，必须要针对具体的学习问题；在某些问题上表现好的学习算法，在另一些问题上却可能不尽如人意。