多变量决策树
若我们将每个属性看成是坐标空间中的一个坐标轴,则
以下图中的西瓜数据
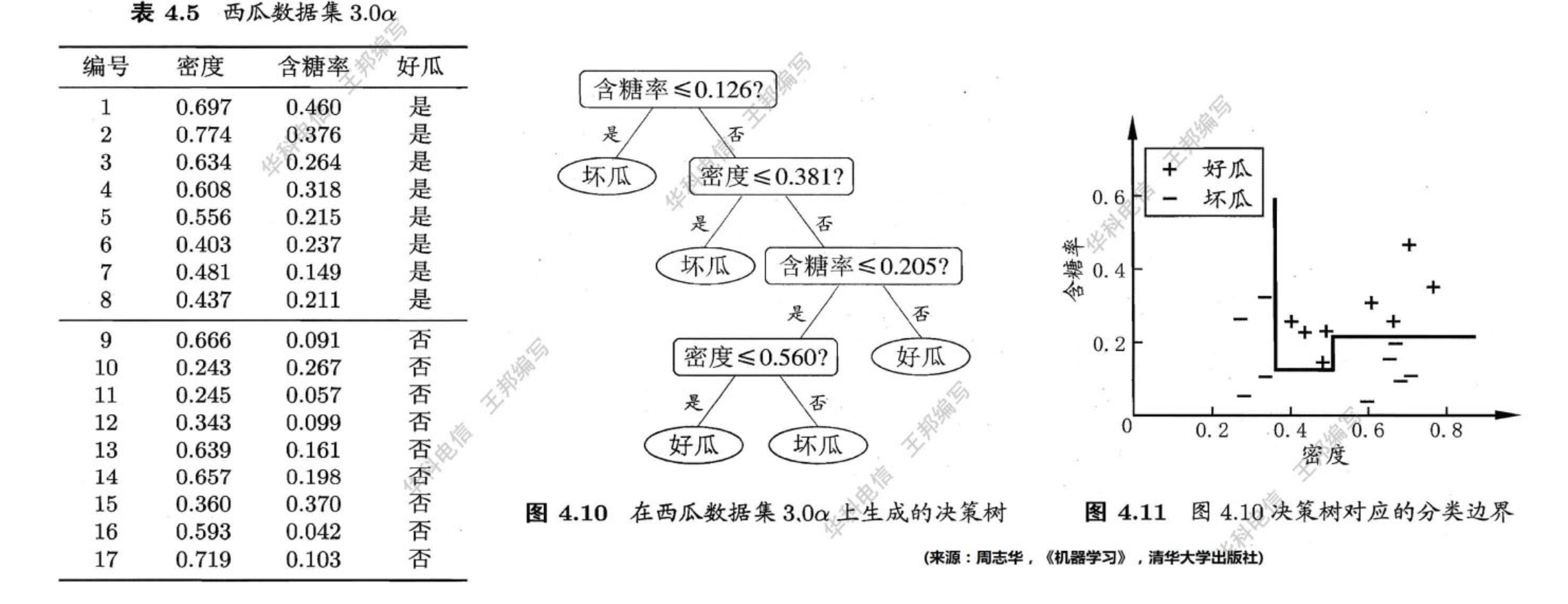
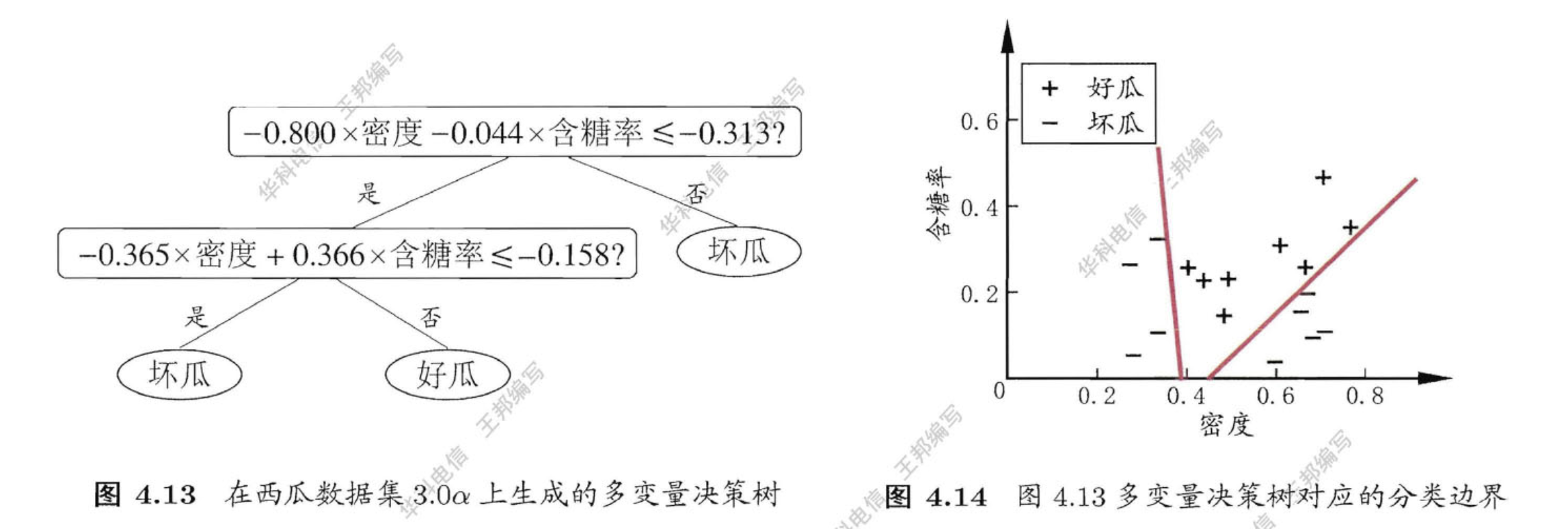
「多变量决策树」(Multivariate Decision Tree)使用斜的划分边界,从而简化决策树模型,以实现斜划分的多变量决策树为例,在此类决策树中,非叶节点不再是仅对某个属性,而是对属性的线性组合进行测试;换言之,每个非叶节点时一个形如
Interactive Graph
Table Of Contents
若我们将每个属性看成是坐标空间中的一个坐标轴,则
以下图中的西瓜数据

「多变量决策树」(Multivariate Decision Tree)使用斜的划分边界,从而简化决策树模型,以实现斜划分的多变量决策树为例,在此类决策树中,非叶节点不再是仅对某个属性,而是对属性的线性组合进行测试;换言之,每个非叶节点时一个形如
