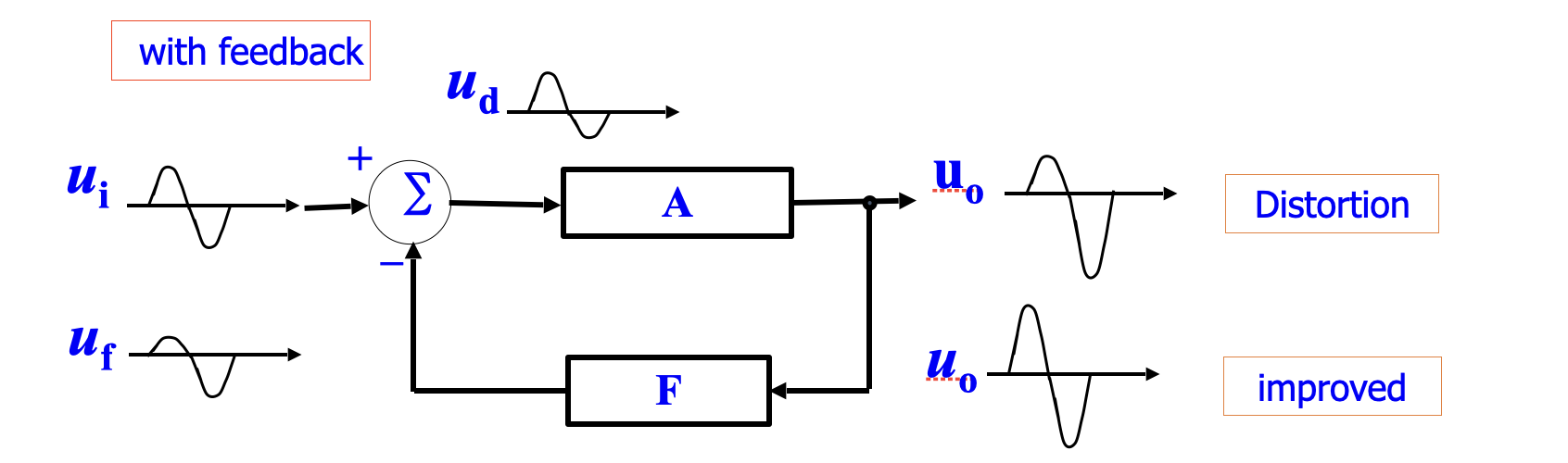
一、反馈的引入
为什么要有反馈?
使用反馈最经典的场景就是在运算放大器中。可以把运放想象为一个差模足够大的差分放大器,差模足够大看似是优点,但其实会导致很多问题。假设某一运放输入电压为
若要使此运放工作在线性放大区,输入的最大电压为
这个量级的电压几乎和噪声一个数量级,因此基本上无法使其工作在线性放大区。
而另一方面,此运放的上限频率只有
由此产生的两个问题
- 增益太大
- 带宽太窄
如何解决这个问题?引入负反馈
使其增益减小,拓展带宽,使得这两个问题同时得到解决(用增益换带宽)
将电路的输出引回输入端,与信号做一个运算,对原来的输入信号产生影响
在本章中只讨论外部电路反馈,不考虑器件内部自身的反馈
1. 反馈
在系统中,输出信号被「反馈网络」以一定比例,与输入信号结合,这样的电路称为「反馈」(Feedback)。反馈被广泛应用于放大电路中。
没有反馈网络存在的放大器称为开环放大器,反之称为闭环放大器。
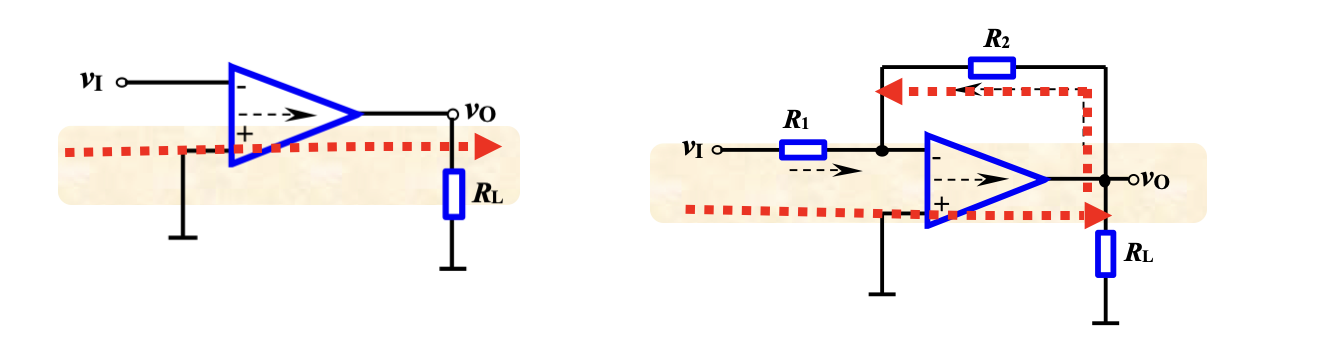
2. 反馈的类型
2.1 正反馈和负反馈
- 正反馈:在反馈下,输入信号相同时,输出增加
- 负反馈:在反馈下,输入信号相同时,输出减少
对于负反馈而言:
- 优点:
- 提高敏感度
- 拓展带宽
- 减小噪声
- 减少非线性失真
- 改善阻抗
- 缺点:
- 增益减小
- 稳定性变差
判断方法:瞬时极性法
在某一时刻,认为信号有一个瞬时的增加量(减少量),然后带着这个变化量分析整个电路的变化状态,直到反馈网络回到输入端,比较反馈信号和原输入信号的正负关系。若反馈信号能与原输入信号产生抵消,则为负反馈,反之为正反馈。
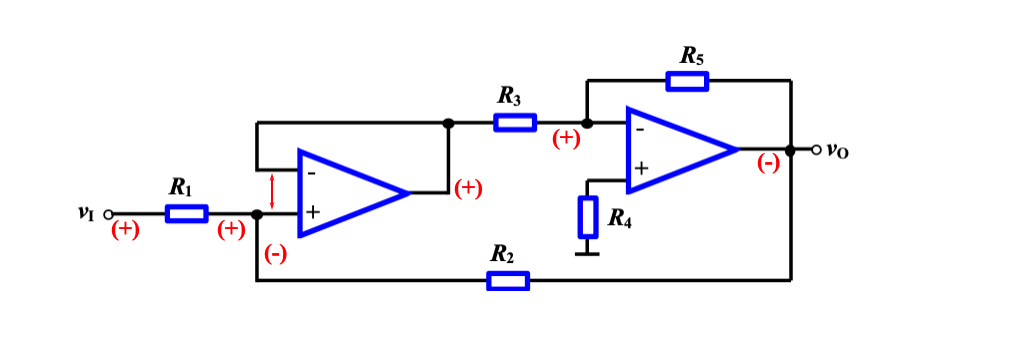
- 通过电容电阻,正负不变
- 通过运算放大器,正端输入正,输出为正,正端输入负,输出为负
- 通过 BJT,
2.2 直流反馈和交流反馈
根据反馈回来的信号是直流还是交流信号,可以将反馈分为「直流反馈」和「交流反馈」。
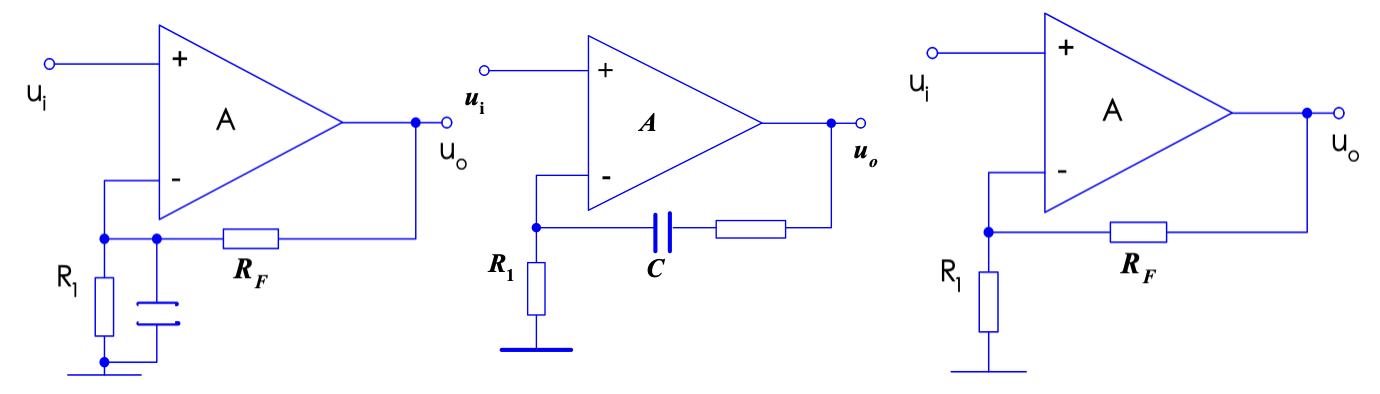
- 图一为旁路电容,使得交流接地,反馈部分只有直流,因此为直流反馈
- 图二为耦合电容,隔断直流信号,只有交流信号反馈,因此为交流反馈
- 图三不存在电容,直流和交流同时通过,因此为交直流反馈
2.3 反馈组态
根据反馈网络与输入端或输出端的连接拓扑关系,可以分为「串联连接」和「并联连接」两种「反馈组态」(Feedback Configuration)。对于一个完整的反馈电路,反馈网络同时连接在输入和输出两端,故可以分为
- 输入串联-输出串联
- 输入并联-输出串联
- 输入串联-输出串联
- 输出并联-输出并联
2.3.1 连接方式
对于输入端而言
- 若反馈信号和输入信号直接连接,则有KCL方程,这是一个电流反馈,即并联
- 若反馈信号和输入信号连在一个元件的不同端上,则存在一个压差,有KVL方程,这是一个电压反馈,即串联
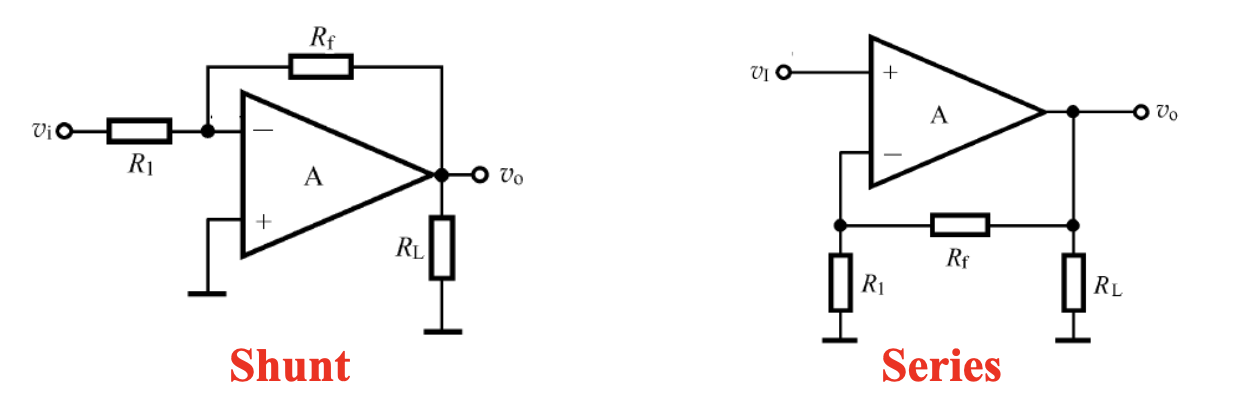
输出端的定义
- 反馈网络接在负载两端,此时相当于电压表,对负载两端电压采样,为并联
- 反馈网络与负载串联,相当于电流表,对负载电流采样,为串联
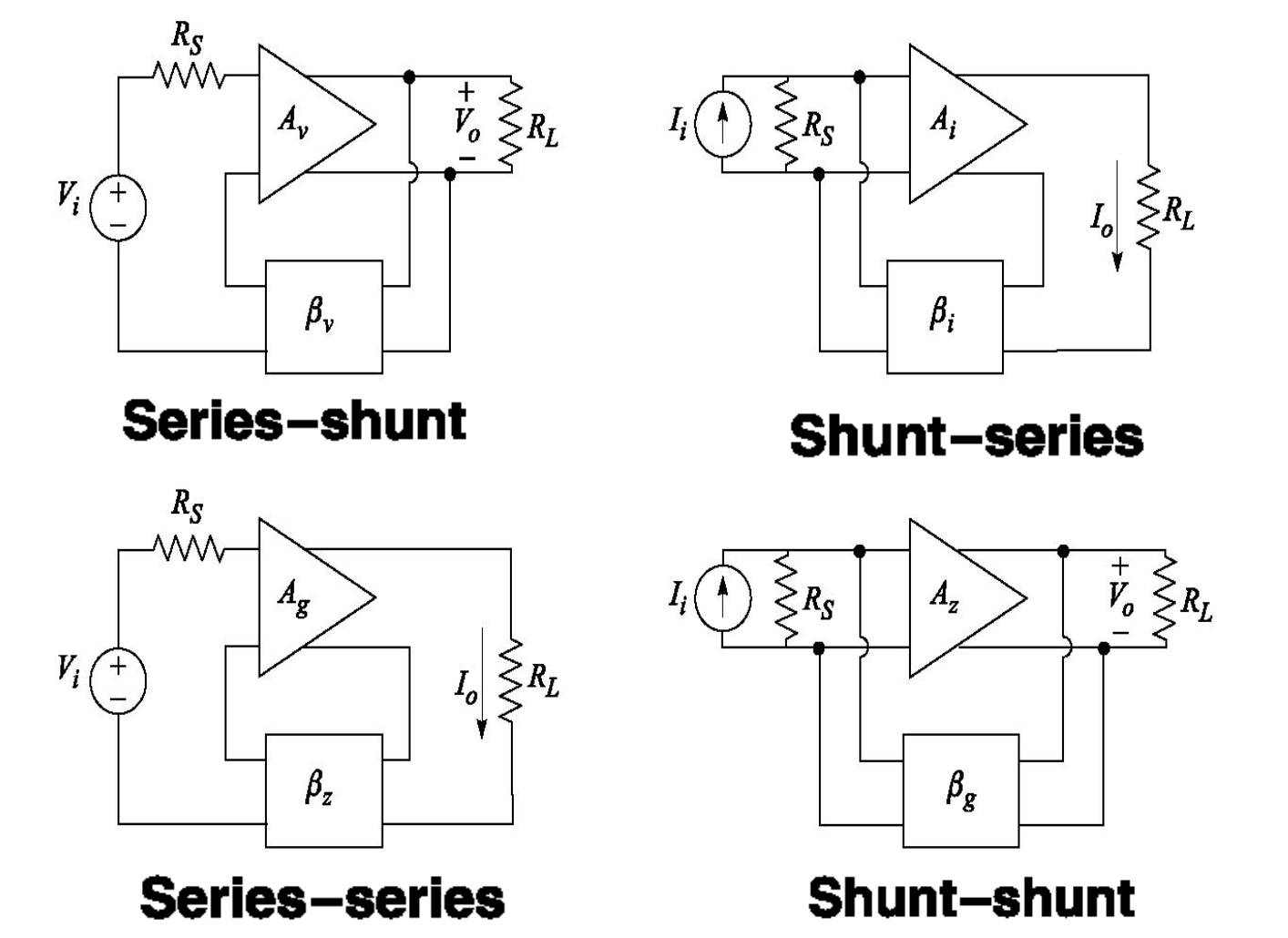
对于输出端,有一种简明的判断方法
- 若负载短路,反馈信号消失,则为并联
- 若负载短路,反馈信号仍存在,则为串联
其实只要是浮地的负载,基本上可以确定是输出串联
本质上,是对输出电压还是电流来「取样」
二、负反馈电路的特点
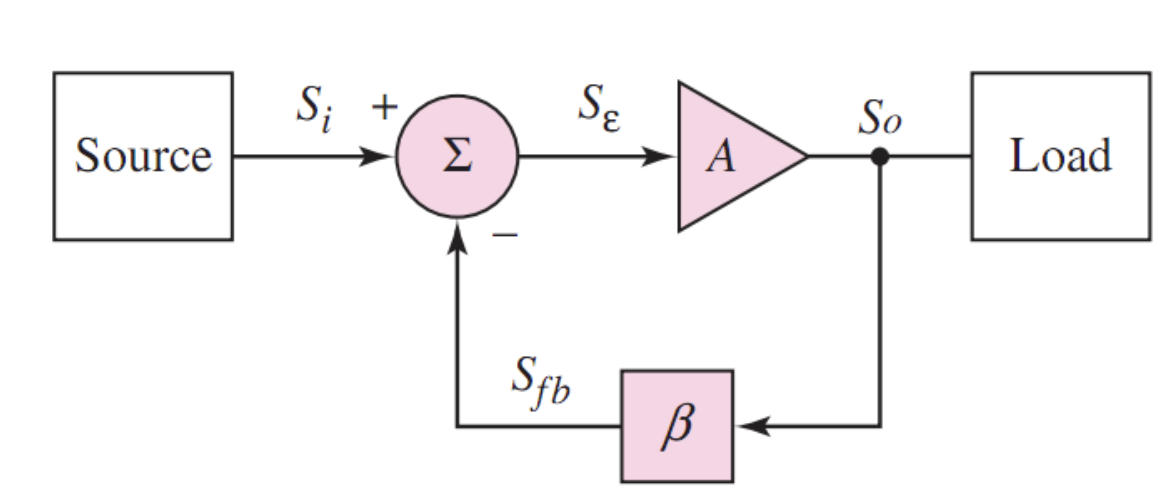
任何一个反馈电路,都可以由上面的关系图来表示。其中,
之前提到负反馈电路存在「减小增益」、「提高灵敏度」、「拓展带宽」和减少非线性失真等特点,接下来根据上面的基本关系,定量地逐一进行分析。
1. 减小增益
根据反馈的定义,反馈信号是输出信号「以一定比例传输回输入端」,因此反馈信号
其中比例系数
而对于放大器有
其中
定义此时输出信号与输入信号的比为「闭环放大倍数」
可以发现,在引入反馈后,电路的放大倍数乘以了
定义
此时,闭环放大倍数为只与反馈网络本身有关的的函数,与放大器本身的放大倍数无关。
2. 增益灵敏度
定义
为增益灵敏度(Gain Sensitivity)
根据公式
将
又由
对于负反馈而言
这说明,由于某些电路参数的变化,导致
3. 带宽拓展
(Bandwidth Extension)
假设放大器的频率响应为单极点,则可以被以下公式描述
其中
假定
与原来的频率响应比较可以发现
即频率上限提高,频率下限降低,带宽被拓展。
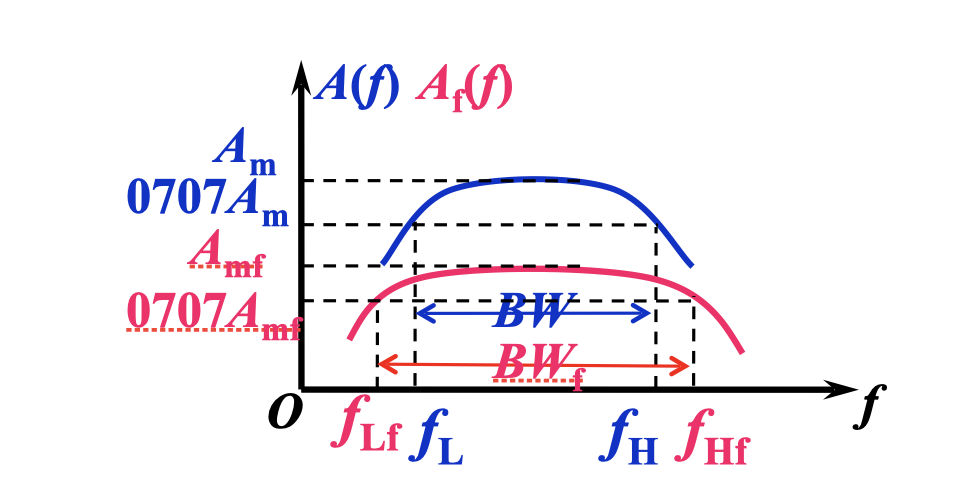
4. 抑制非线性失真
在原有放大器工作时,若线性区过载,可能导致非线性失真。
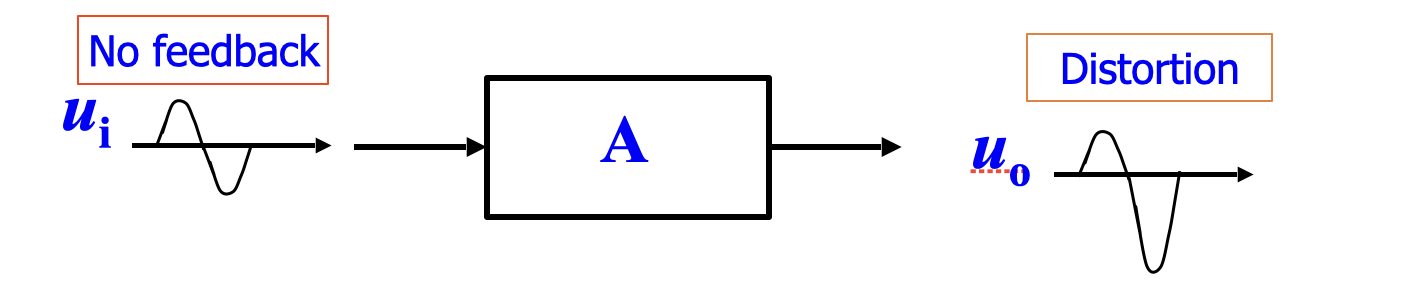
在不改变输入信号的情况下,如何改善失真?此时可以引入负反馈,让失真的输出信号与原输入信号生成一个更「线性」的净输入信号
5. 阻抗改善
根据反馈串并联关系的不同,阻抗改善的讨论也不同。
- 输入串联-输出并联(Series-Shunt)
- 输入并联-输出串联(Shunt-Series)
- 输入并联-输出并联(Shunt-Shunt)
- 输入串联-输入串联(Series-Series)
在接下来的几部分,将对四种反馈结构的阻抗即增益作讨论。
四种组态的判别方法
输入端
反馈网络和输入信号连接到同一端,说明是并联组态,如下图
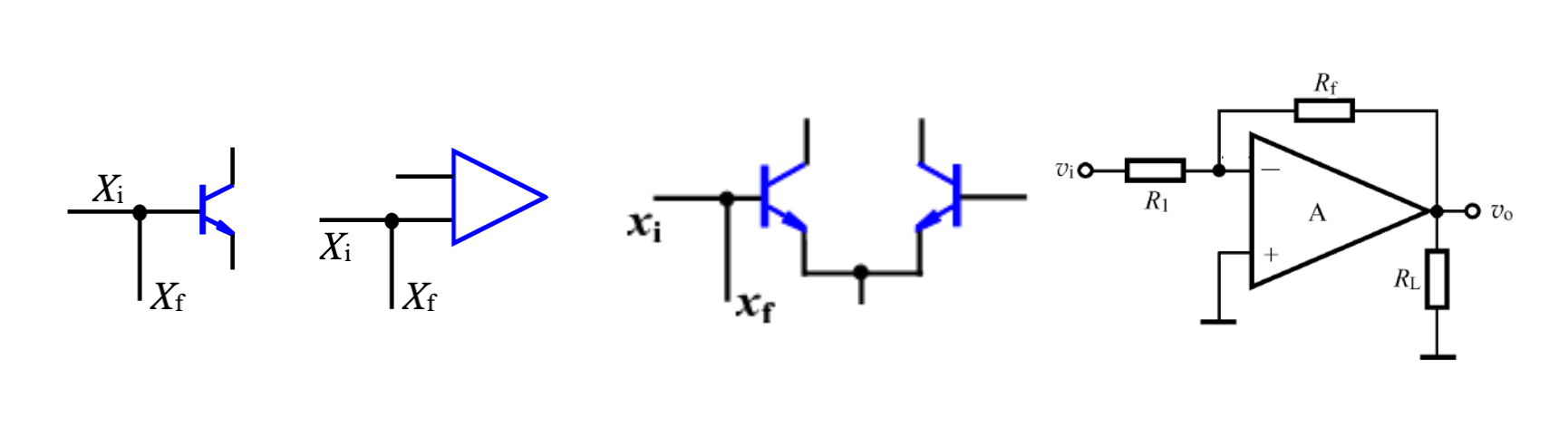
反馈网络和输入信号连接到不同端,说明是串联组态,如下图

输出端
若负载短路,反馈信号为零,说明是并联组态
若负载短路,反馈信号仍存在,说明是串联组态
三、输入串联-输出并联
输入串联-输出并联电路(Series-Shunt),观察其电路结构可以发现,由于输出端为并联,因此相当于像是个电压表一样「采集了输出端电压信号」,传输给输入端时,与输入端串联,因此实现负反馈的工作原理,即
这一工作过程,是采集输出端的电压信号,与输入端的电压信号做运算,因此这种组态也被称为电压放大器。(Voltage-Voltage Amplifier)
根据之前的反馈电路基本结构,画出小信号模型。
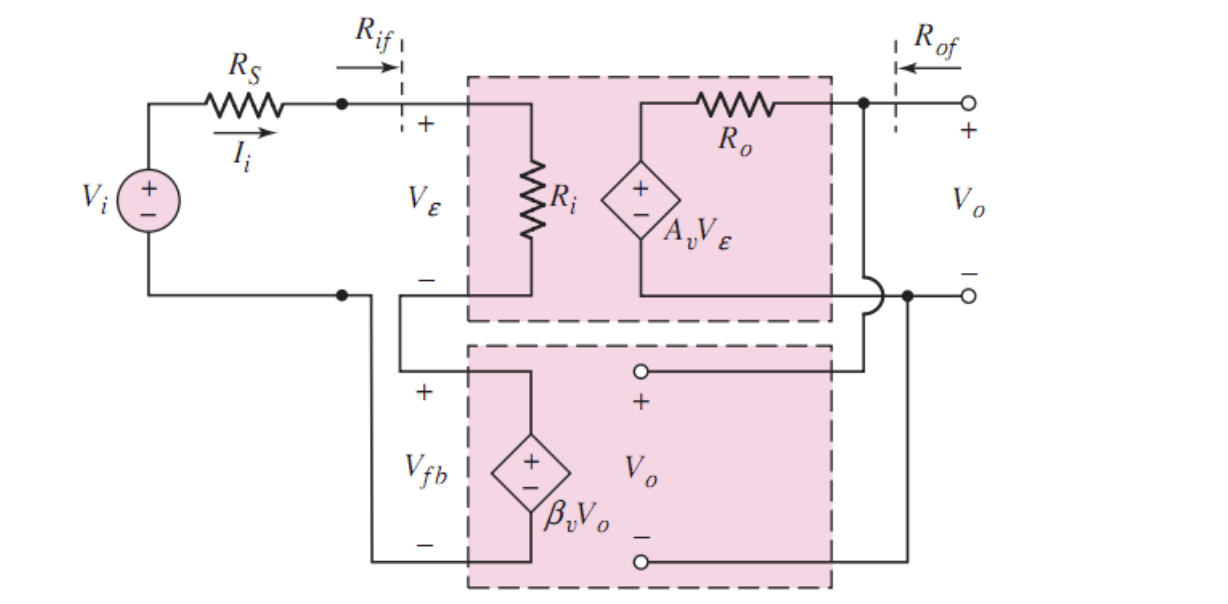
由于信号为电压信号,则根据反馈的分析有
1. 输入阻抗
根据输入阻抗的定义,先表示出输入电压
此时输入电流为「从放大器两端看进去的电流」,因此输入电流应表示为加在放大器上的电压信号比输入阻抗
定义此时有反馈的输入电阻为「闭环输入电阻」,记为
结论:串联输入会增大输入电阻,即乘上了
2. 输出阻抗
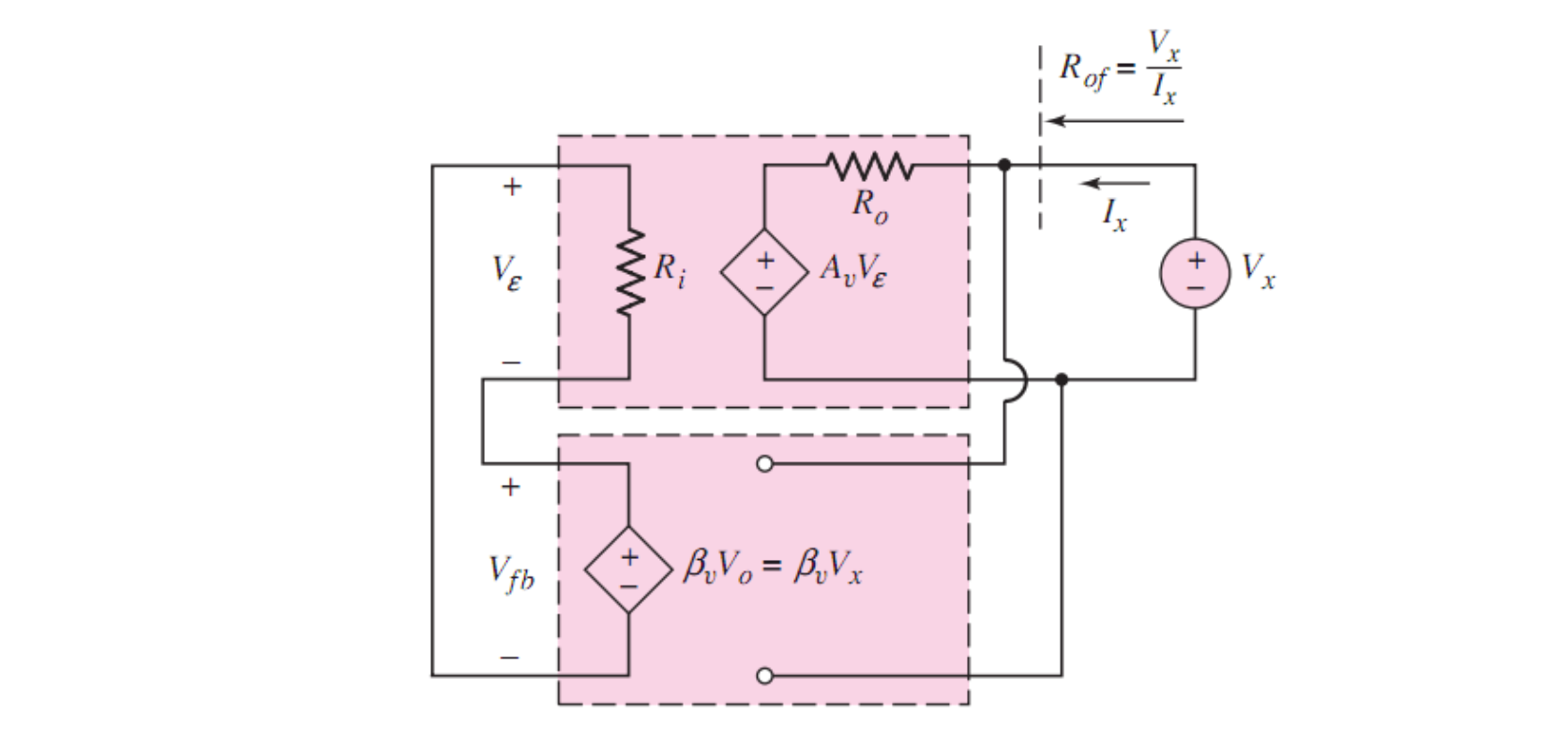
再考察输出电阻,记输出端电压和电流分别为
对于电流而言,电流
定义此时有反馈的输出电阻为「闭环输出电阻」,记为
结论:并联输出会减小输出电阻,即除以了
3. 闭环放大倍数
由负反馈三大方程
可以直接得到闭环电压增益
结论:会减小电压增益,即除以了
四、输入并联-输出串联
输入串联-输出并联电路,观察其电路结构可以发现,由于输出端为串联,因此相当于像是个电流表一样「采集了流过输出端的电流信号」,传输给输入端时,与输入端并联,因此实现负反馈的工作原理,即
这一工作过程,是采集输出端的电流信号,与输入端的电流信号做运算,因此这种组态也被称为电流放大器(Current-current Amplifier)
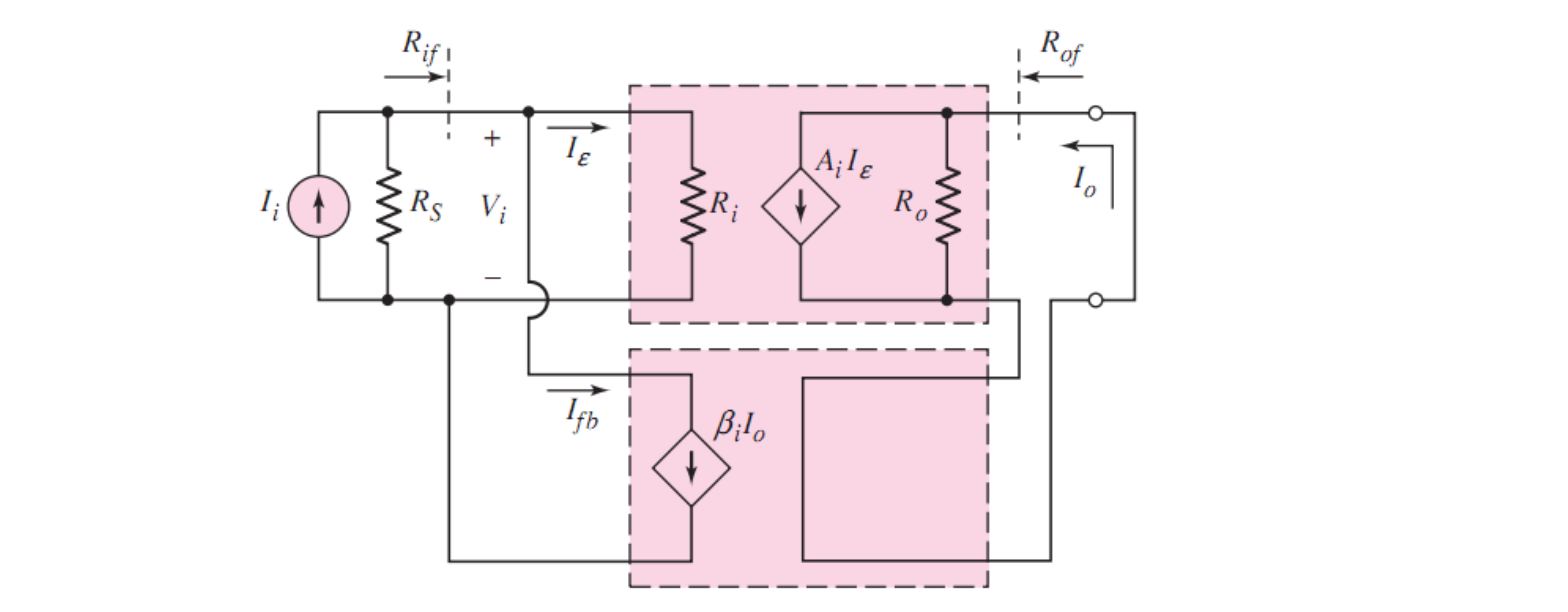
1. 输入阻抗
要求输入阻抗,根据定义就要求输入电压和电流
首先写出输入电压的表达式
再求输入电流
由反馈的三大方程,可以很容易得到
得到
因此输入电阻为
结论:输入并联-输出串联会减小输入电阻,即除以了
2. 输出阻抗
再考察输出电阻,记输出端电压和电流分别为
由反馈的三大方程,可以很容易得到
得到关系
然后再表示出输出电压
最后得到输出阻抗
结论:输入并联-输出串联会增大输出电阻,即乘上了
3. 闭环电流增益
由
得到闭环电流增益
结论:输入并联-输出串联会减小电流增益,即除以了
五、输入串联-输出串联
根据前面两种组态的分析,输出端串联表示采集电流,输入端串联表示电压运算。因此这种放大器称为电压-电流放大器(Voltage-current Amplifier)或跨导放大器(Transconductance Amplifier)
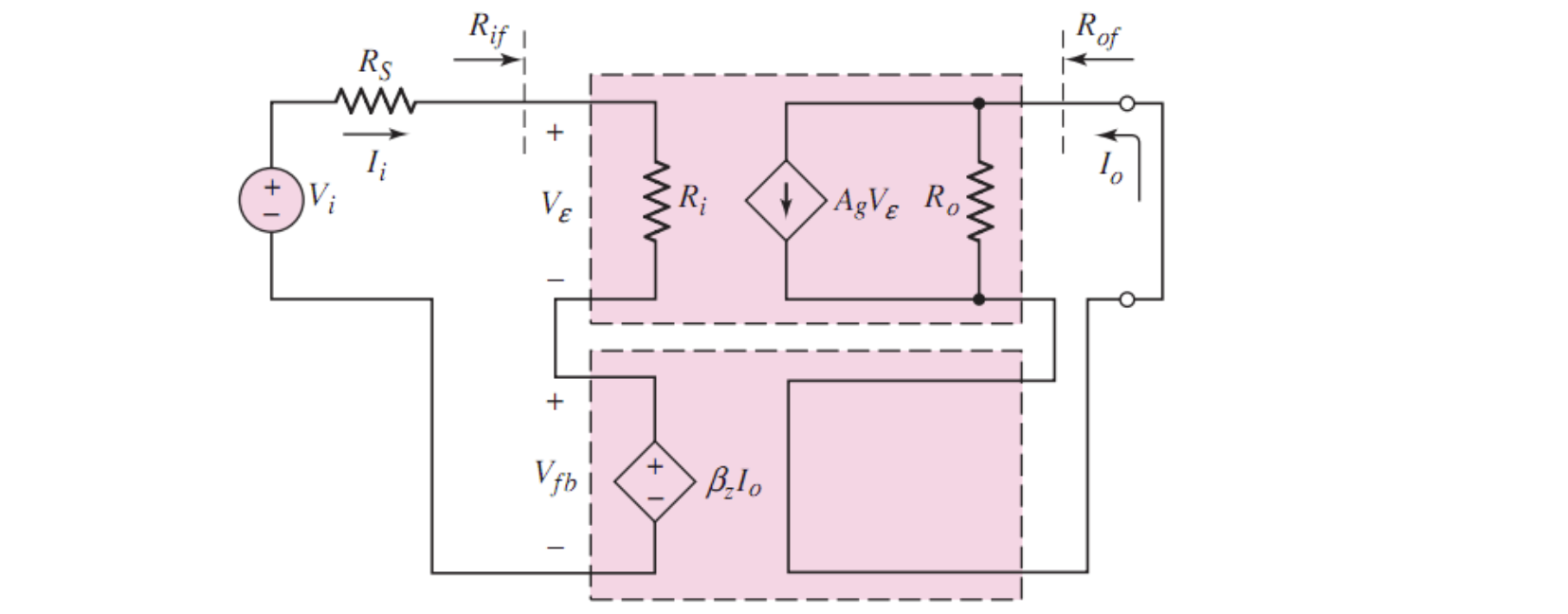
1. 输入阻抗
输入电流显然可以直接表示为
电压为
因此输入阻抗为
结论:输入串联-输出串联会增大输入电阻,即乘上了
2. 输出阻抗
再考察输出电阻,记输出端电压和电流分别为
由输入端置零,此时
而对于电压,相当于恒流源内部的内阻两端电压
可以直接表示出输出阻抗
结论:输入串联-输出串联会增大输出电阻,即乘上了
3. 闭环增益
输入串联-输出串联是输出端电流和输入端电压的反馈。因此在表示闭环增益时,表示为跨导形式
对于输入端
对于输出端
在根据小信号模型可以写出
综上直接写出闭环增益
可以发现其量纲为电导。
结论:输入串联-输出串联会减小增益,即除以了
六、输入并联-输出并联
根据前面两种组态的分析,输出端并联表示采集电压,输入端并联表示电流运算。因此这种放大器称为电流-电压放大器(Current-voltage Amplifier)或互阻放大器(Transresustabce Amplifier)
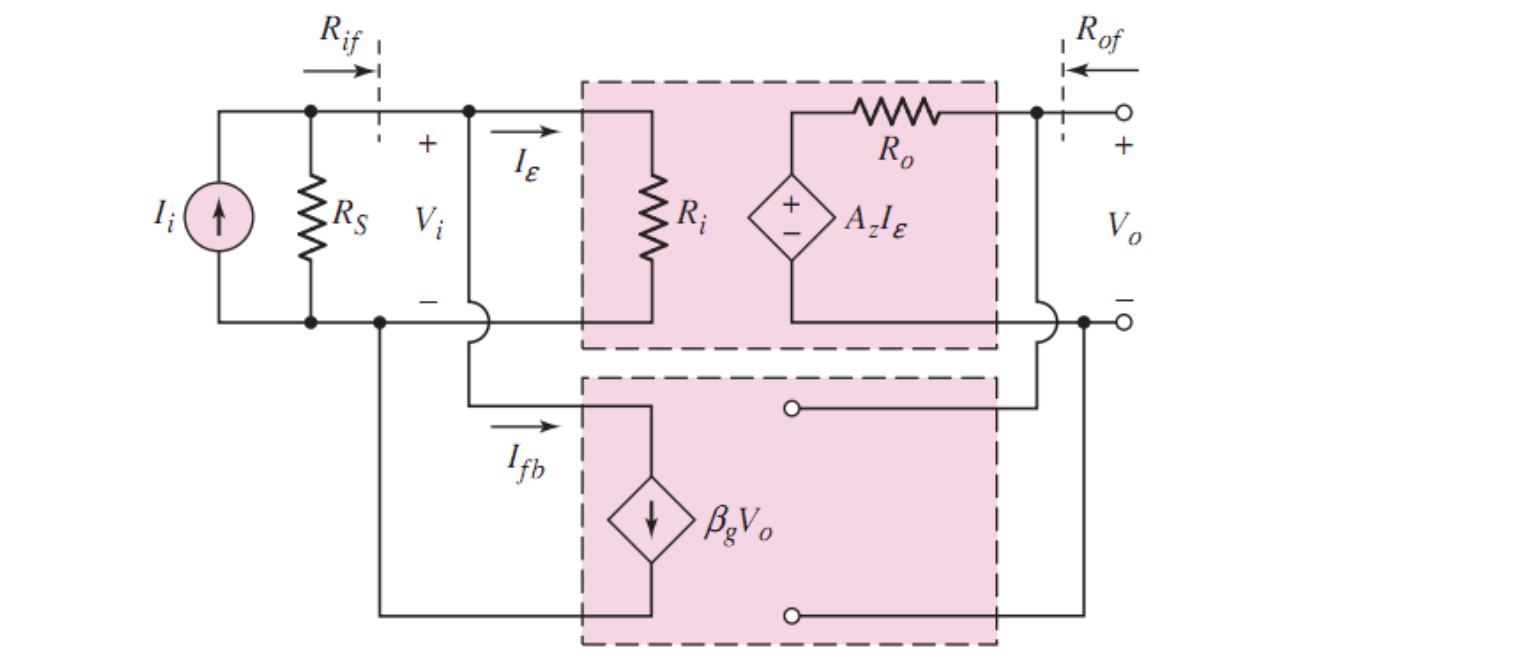
1. 输入阻抗
输入电流被分为两部分,即
输入电压就是放大器输入电阻两端的电压
因此输入阻抗可以表示为
结论:输入并联-输出并联会减小输入电阻,即除以了
2. 输出阻抗
再考察输出电阻,记输出端电压和电流分别为
由输入端置零,此时
而对于输出端有
即
代入
结论:输入并联-输出并联会减小输出电阻,即除以了
3. 闭环增益
输入并联-输出并联是输出端电压和输入端电流的反馈。因此在表示闭环增益时,表示为互阻形式
对于输入端
对于输出端
根据小信号模型可以写出
综上直接写出闭环增益
可以发现其量纲为电阻。
结论:输入并联-输出并联会减小增益,即除以了
七、深度负反馈分析
通常来说,放大器如运算放大器的
根据此近似得到重要关系
由此重要关系,可以得到几个结论。
根据定义,
又因为
根据净输入定义
综上得到两个在深度负反馈下的重要结论
- 输入近似等于反馈
- 净输入近似为零
在接下来的分析中,将会频繁使用这两个结论进行分析和化简。值得一提的是,在「运算放大器」一章中提到的「虚短虚断」,本质上就是由这两个结论推导得到的。接下来根据反馈组态的不同举几个例子进行深度负反馈分析。
1. 电压放大器
如图,是一个电压放大器。求其闭环电压增益
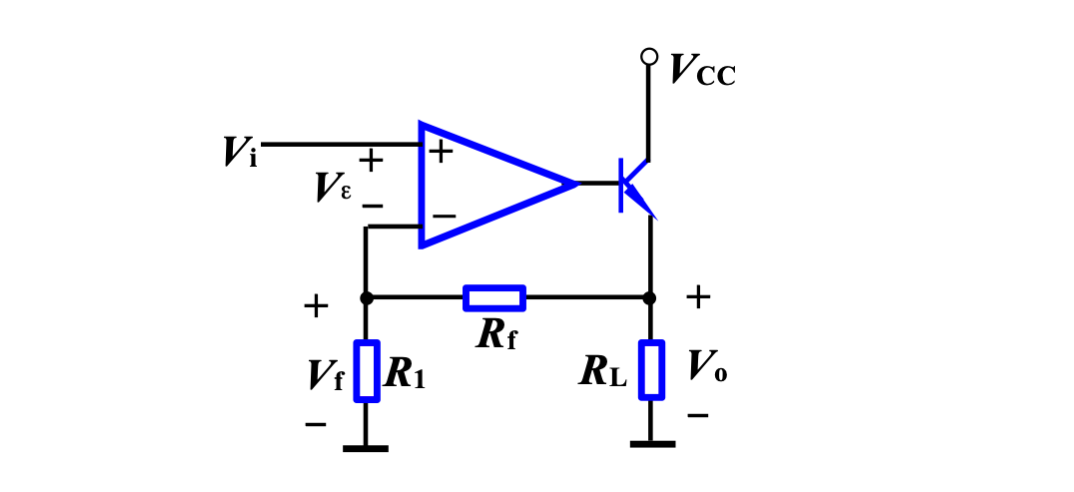
根据深度负反馈的输入信号等于反馈信号特性,则根据定义
由深度负反馈净输入为零特性,运算放大器两端均无电流,流过
因此其闭环电压增益为
2. BJT 单管放大器
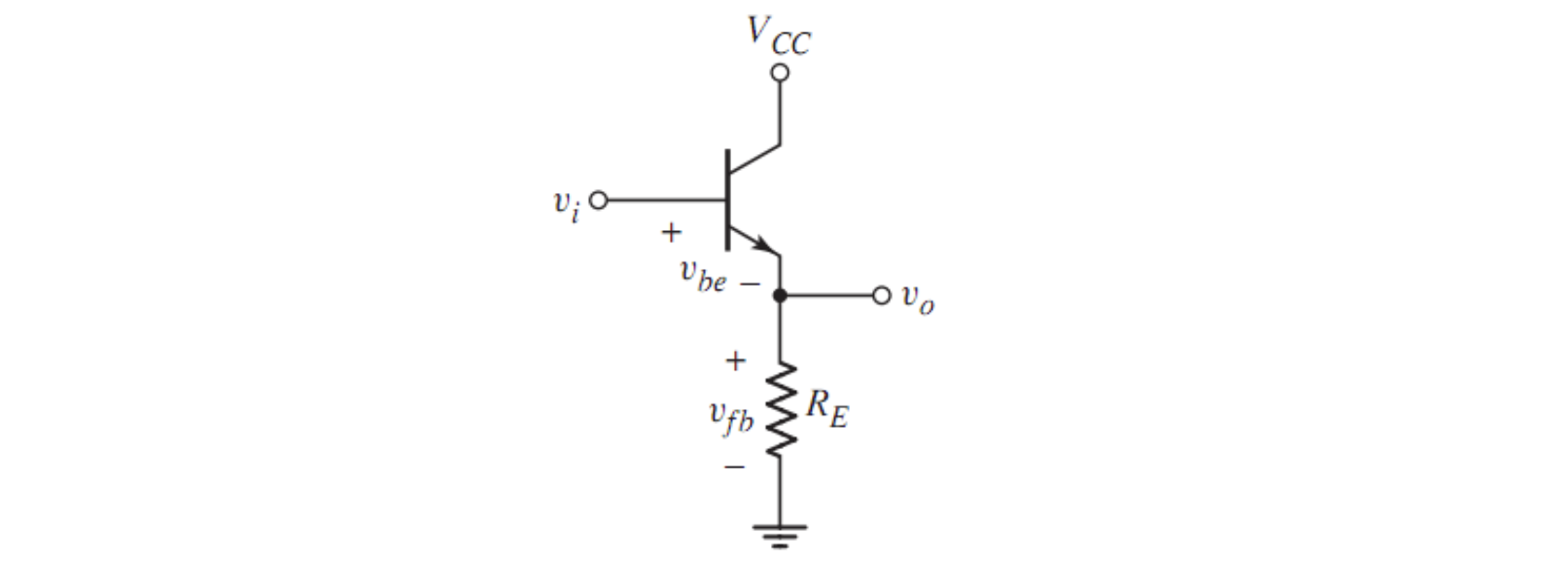
与上面的分析类似,可以直接写出
某种意义上来说,这里的 BJT 管在深度负反馈下也满足「虚短虚断」,即
但在 BJT 一章我们很清楚,B-E 两端在工作时必然存在
其实这里的深度负反馈是一种交流分析,因此我们默认直流分量已经「打开」了B-E两端,即那
3. 电流放大器
求下图电路的闭环电流增益和电压增益
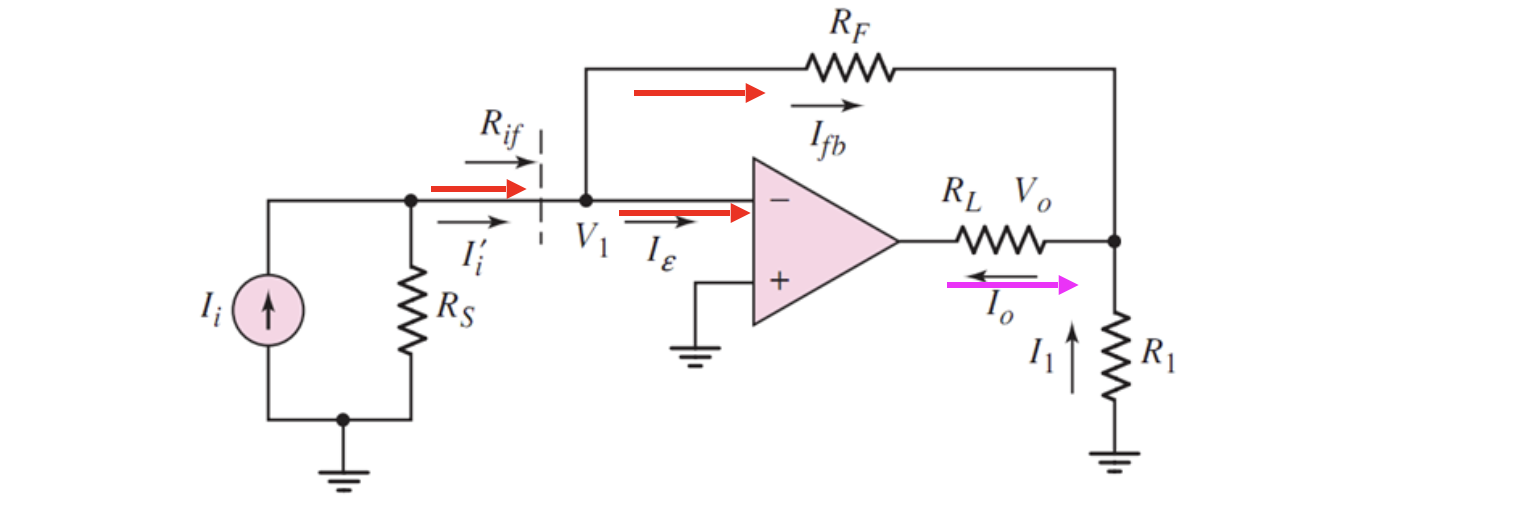
根据深度负反馈的「反馈信号等于输入信号」
由虚短,运放的反相输入端接地,则
因此闭环电流增益可以表示为
接下来求电压增益。由于
由上面已经求得的电流增益
4. BJT 电流放大器
求此电流放大器的闭环电流增益和电压增益
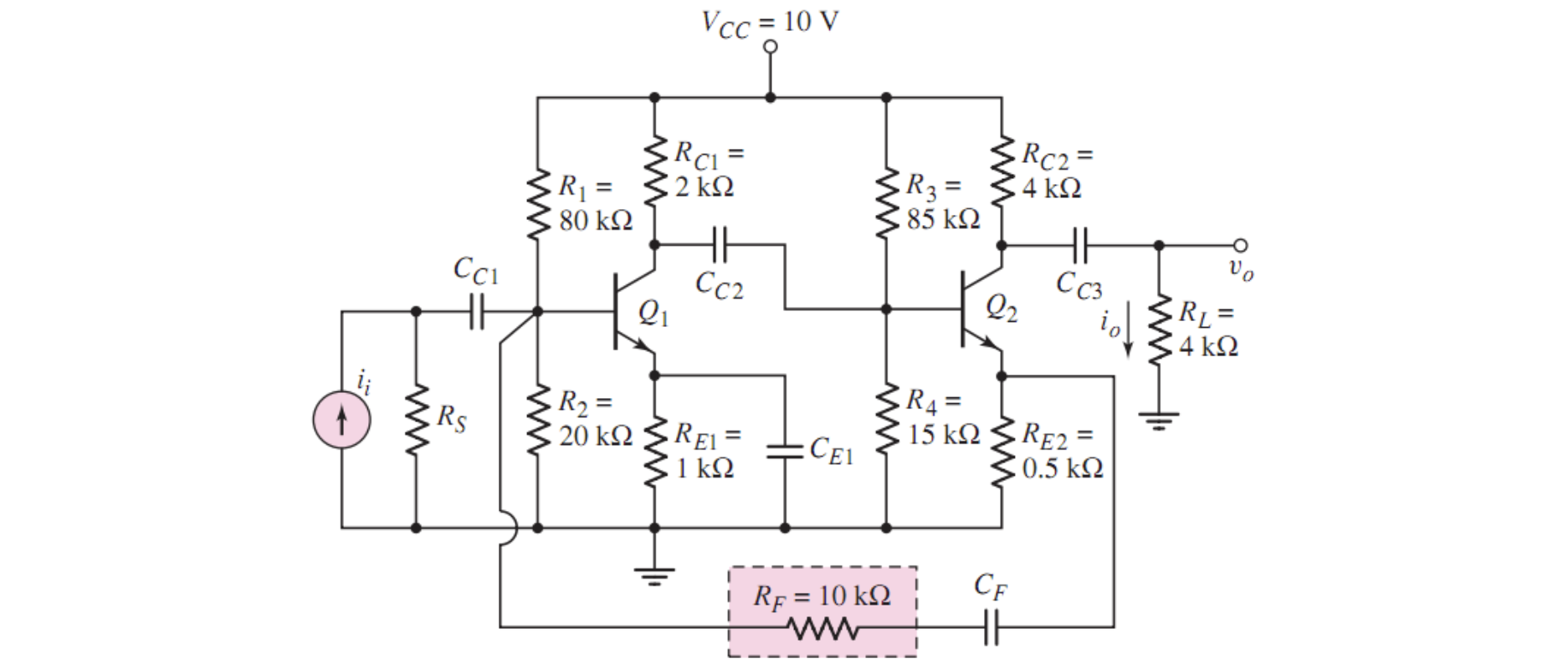
不难判断,是输入并联-输出串联组态的负反馈网络。先求电流增益
由于交流把
而
得到闭环电流增益
八、环路增益
对于通常的反馈电路来说,构成了净输入-放大器-反馈网络-净输入的环路
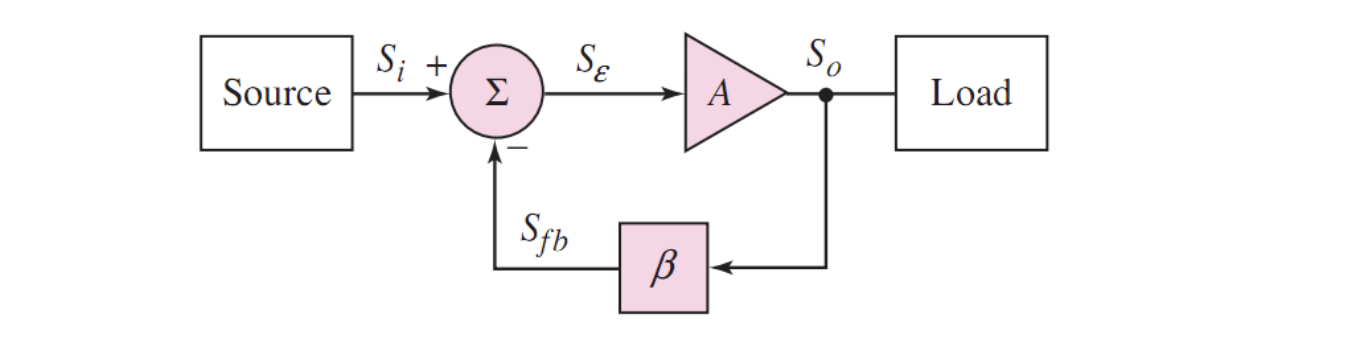
我们想要分析,一个信号在此环路循环一次后发生了什么变化,即探讨反馈电路的「环路增益」
首先需要在某处断开环,防止无限循环;然后将输入信号置零。比如下图
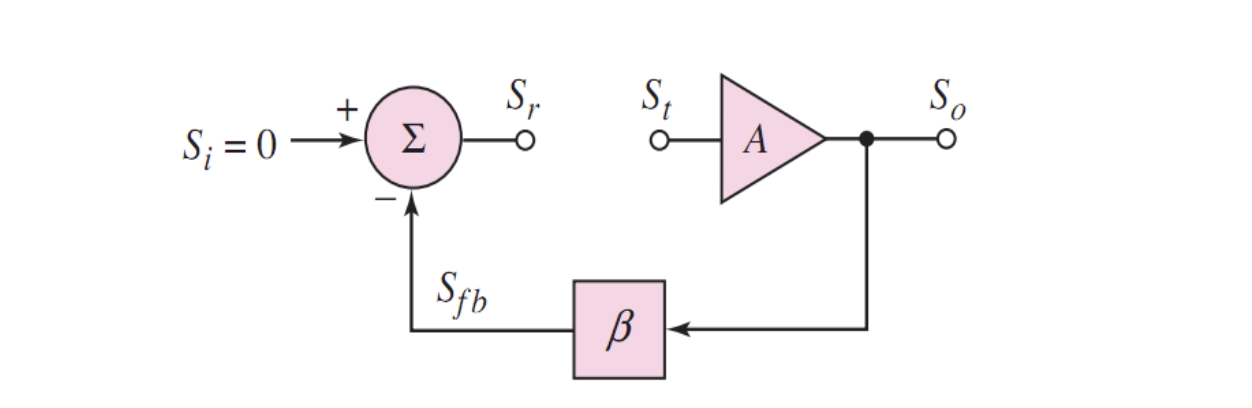
那么环路增益等于信号
注意:环路增益和闭环增益不同!
八、反馈稳定性
此部分内容十五章还会再次讲到
根据频率响应部分的知识,放大器本身的放大倍数是频率的函数,因此频率改变时,一个含有反馈电路的放大电路的闭环增益也会随之改变。在某些情况下,甚至会改变反馈的极性。接下来,我们分析频率变化对反馈电路工作的影响。
设反馈网络为纯阻性网络,
之前已经定义环路增益
其中
1. 自激振荡
负反馈的定义是净输入小于输入。因此只有当三个信号同相,才能保证满足关系
但是当频率变化时,因为
根据方程
或者从另外一个角度分析,由于
在不外加输入信号时,电路自行产生了持续的震荡。这种现象称为「自激」
根据刚刚的分析,产生自激的条件是
2. 自激的条件分析
根据频率响应方面的知识,一阶电路移相最大值 90 度,无法满足自激条件,因此一阶电路不可能出现自激
对于二阶电路,频率趋于无穷大时,移相达到最大值 180 度。此时
当电路为三阶,就有可能出现震荡了
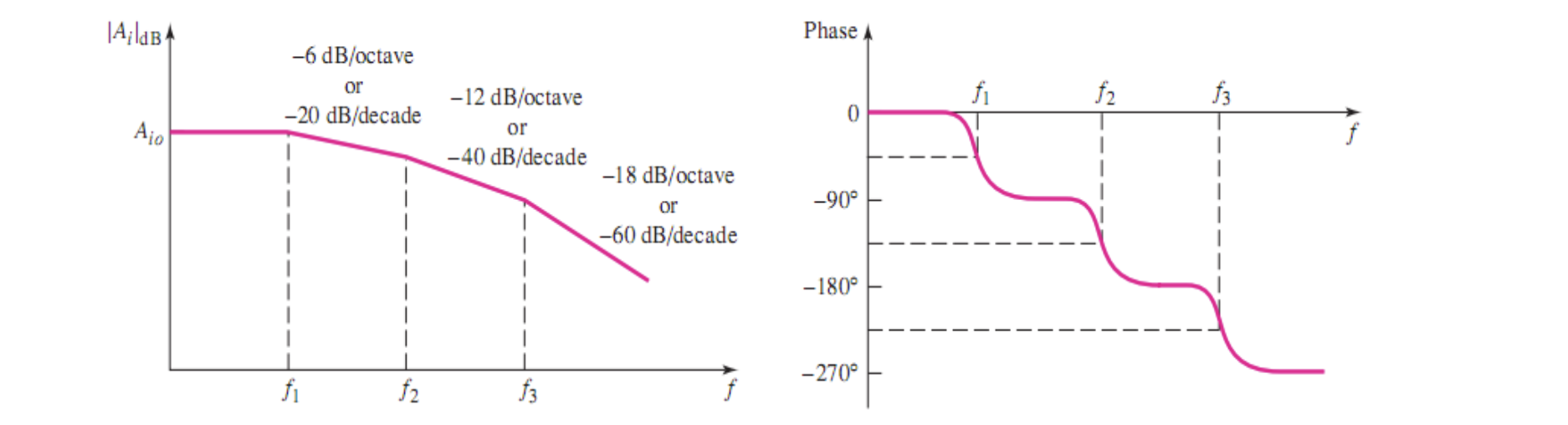
3. 避免自激
为了防止自激,必须破坏
在自激破坏的情况下,有关系
称
考试要求
连接反馈
闭环增益,闭环电压增益
除了反馈本身,其他题目之中可能时刻参杂着反馈。