一、信源编码概念
信源编码是以提高通信的有效性为目的编码。尽可能少的比特传递尽可能多的信息量。通常通过压缩信源的冗余度来实现。
采用的一般方法是压缩每个信源符号的平均比特数或信源的码率。同样多的信息用较少的码率来传送,使单位时间内传送的平均信息量增加,从而提高通信的有效性。
信源编码的基本途径有两个:
- 使序列中的各个符号尽可能地互相独立,即解除相关性;
- 使编码中各个符号出现的概率尽可能地相等,即概率均匀化。
信源编码的基础是信息论中的两个编码定理:
- 无失真编码定理
- 限失真编码定理
无失真编码只适用于离散信源;对于连续信源,只能在失真受限制的情况下进行限失真编码。本章首先介绍信源编码的相关概念以及信源编码定理,然后描述编码方法。
1. 无失真信源编码
无失真信源编码要求精确地复现信源的输出,并且保证信源的全部信息无损的送给信宿。
研究方法:
- 只考虑有效性,不考虑可靠性
- 将信道编解码看成一个无噪无损信道
解决两个问题:
- 描述信源的输出,计算它产生的信息量;
- 表示信源的输出,即信源编码(无失真/限失真)与信宿对通信质量的要求有关
因为,不考虑抗干扰问题。所以,数学描述比较简单。如下图所示
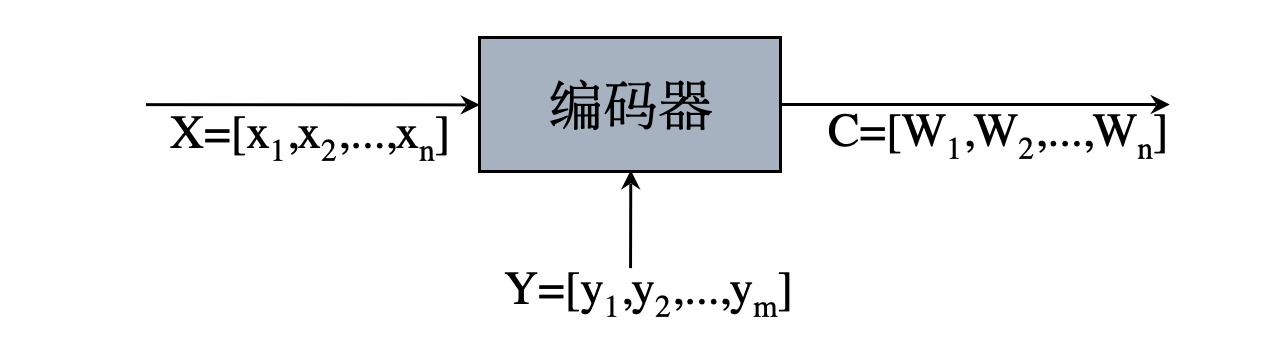
其中:
- 信源符号集
- 码符号集
, 共 有 - 码字集合
编码器的作用:
将信源符号集
输出符号序列就是码字,与信源符号一一对应。
例
例 设有二元信道的信源编码器,其信源概率空间为
二元信道是常用信道,它的信道基本符号集为
| 信源符号 | 信源符号概率 | 码 1(定长码) | 码2(变长码) | 码 3(奇异码) | 码 4(奇异码) |
|---|---|---|---|---|---|
2. 码的分类与性质
2.1 定长码和变长码
根据码长,可分为两类:
- 「定长码」:码中所有码字的长度都相同,如上例中的码 1
- 「变长码」:码字长短不一,即码符号个数不同,如上例中的码 2
2.2 奇异码
若一种码中的所有码字都互不相同,则称此分组码为「非奇异码」,否则称为「奇异码」。非奇异码只是正确译码的必要条件,因为当码字排在一起时还有可能出现奇异性。
表中,
2.3 唯一可译性
设信源符号
映射为
的码称为原码的「
2.4 即时码
定义
无需考虑后续的码符号即可以从码符号序列中译出码字,这样的唯一可译码称为「即时码」。
| 信源符号 | ||
|---|---|---|
定理
设
一个唯一可译码成为即时码的充要条件是其中任何一个码字都不是其它码字的前缀。
证明
充分性:因为如果没有一个码字是其它码字的前缀,则在接收到一个相当于一个完整码字的码符号序列后,便可立即译码,而无须考虑其后的码符号。
必要性:用反证法。若设
即时码的构造
对于
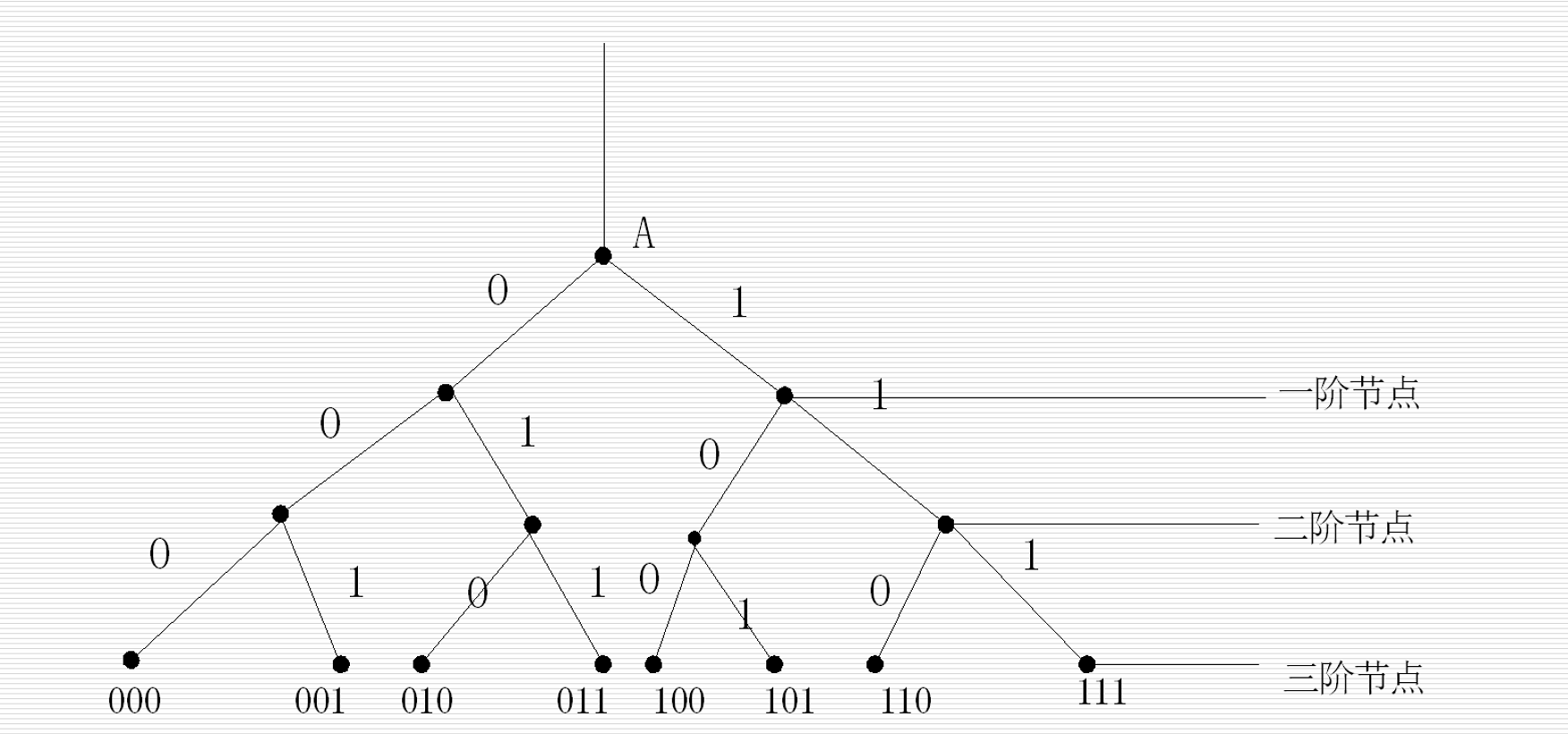
考虑一个树有
- 整树:码树的各个分支都延伸到最后一级端点,此时,将共有
- 非整树:码树中存在分支,没有延伸到最后一级端点,此时,将少于
2.5 唯一可译定长码的存在条件
定长码中每个码字长度相等,所以只要定长码是非奇异码,则必为唯一可译码。对一个简单信源
其中,
2.6
对
两边取以
注意,上面两边是编码前后,等概分布时的信息量。对于前者,我们不能保证,而后者,可以通过恰当的编码方式使其取最大。或写成
其中
例题
英文电报有
这就是说,每个英文电报符号至少要用
3. 定长编码定理
满足
的定长编码虽然可以保证无失真的编码,但是平均码长很大,编码的效率很低。下面介绍的定长编码定理讨论了编码的有关参数对译码差错的限制关系。
3.1 定理
设离散无记忆信源
的熵为
码符号集
则当
则当
3.2 渐进等分割性和
由弱大数定理知:只要
故,扩展序列可分为两个互补的子集:
的序列称为「
性质 1
对于任意小的正数
即
性质 2
如果
性质 3
随着
3.3 理解
定长信源编码定理的意义:
信源经过定长编码后,所能携带的最大信息量,一定要大于信源所携带的平均信息量
3.4 提高编码效率
一般情况下,信源符号并非等概率分布,而且相互关联,故信源极限熵
这时在定长编码中每个信源符号平均所需的二元码符号大大减少,从而提高了编码效率;
例如,以英文电报为例,资料显示,英文电报信源的极限熵
4. 编码信息率与信息传输率
4.1 编码信息率
编码后平均每个信源符号能载荷的最大信息量称为「编码信息率」。若对长为
其中
4.2 信息传输率
平均每个码元载荷的信息量称为「信息传输率」
单位为比特/码符号
4.3 编码效率
信源的每个符号载荷的信息量与编码后每个信源符号能荷载的最大信息量之比称为「编码效率」,即
对于等长编码有
编码效率一定是小于或等于
4.4 编码效率与扩展次数
定长编码定理中,只有在
4.5 例
设离散无记忆信源
采取等长二元编码时,要求编码效率
由
得
二、变长编码
考编码效率,信息传输率不好说。但是概念还是要搞清楚的,剩余度不考
1. 变长编码
定长编码在理论上可以达到很高的编码效率,但是从上例中可以看到,在编码效率、错误概率要求较高的情况下,扩展次数
当
在实际过程中,普遍使用变长编码。
特点
在码符号序列长度
完全无失真的编码。
要求
变长码要满足唯一可译码的条件,它必须是非奇异码,而且任意有限长
为了能够即时译码,变长码必须是即时码。
2. 克拉夫特不等式
克拉夫特不等式描述了信源符号数和码字长度之间应满足什么条件才能构成即时码。
设信源符号集
称上式为「克拉夫特不等式」。剪枝的总数不能超过总枝。
3. 麦克米伦不等式
可将克拉夫特不等式的结果推广到唯一可译码的情况:在前一定理所给定的条件下,唯一可译码存在的充要条件是
称上式为「麦克米伦不等式」。其中,
例如:码字中有两个码字长度相同,则这两个码字无论是否相同,都可能使不等式成立。但是,当这两个码字相同时,显然不可能是唯一可译码。
4. 平均码长
设有信源
编码后的码字分别为
5. 香农第一定理
5.1 定义
设离散无记忆信源为
其信源熵为
其熵为
记
当
或
其中,
5.2 推广到普通信源
变长无失真信源编码定理可以推广到平稳遍历的有记忆信源,一般离散信源或马尔可夫信源,有
其中,
6. 变长编码的编码信息率
定义变长编码的「编码信息率」为:
它表示编码后平均每个信源符号能载荷的最大信息量。因为不是信道上的,所以用
香农第一定理又可以表述为:
- 若
- 若
7. 信息传输率
从信道角度看,信道的信息传输率
因为
当平均码长
8. 编码效率和剩余度
8.1 定义
定义
为「编码效率」。编码效率
为码的「剩余度」
8.2 例题
设有一离散无记忆信源
其熵为
用二元符号
则平均码长为
对信源
| 即时码 | ||
|---|---|---|
这个码的平均长度为
信源
其编码效率为
得
比 特 二 元 码 符 号 比 特 二 元 码 符 号 比 特 二 元 码 符 号 比 特 二 元 码 符 号
对于同一信源,要求编码效率都达到 96%,比较:
- 变长码只需要对二次扩展信源(
- 而等长码则要求
很明显,用变长码编码时,
三、三种常见的离散信源编码
只考虑三种编码方法就可以了。
1. 香农编码
1.1 过程
将信源发出的
按下式计算第
对于上式而言,若乘
这是没有进行
为了编成唯一可译码,首先计算第
特别的,
1.2 例题
| 消息序号 |
消息概率 |
累加概率 |
代码组长度 |
二进制代码组 | |
|---|---|---|---|---|---|
先计算第
取整,故
将累加概率
故变换成二进制数为
由上表可以看出,一共有
平均码长为
平均信息传输率
编码效率很低下,因此主要是理论意义,诠释了变长编码定理。
2. 霍夫曼编码
2.1 过程
将信源发出的
用
把缩减信源
依次继续下去,直至信源最后只剩两个符号为止。将这最后两个信源符号分别用二进制符号“
从最后一级缩减信源开始,向前返回,就得出各信源符号所对应的码符号序列,即相应的码字。这样的编码称为「霍夫曼编码」,这种编码方式在无记忆编码中是最佳的。
2.2 例题
设有离散无记忆信源
对其进行霍夫曼编码,编码过程如下表所示
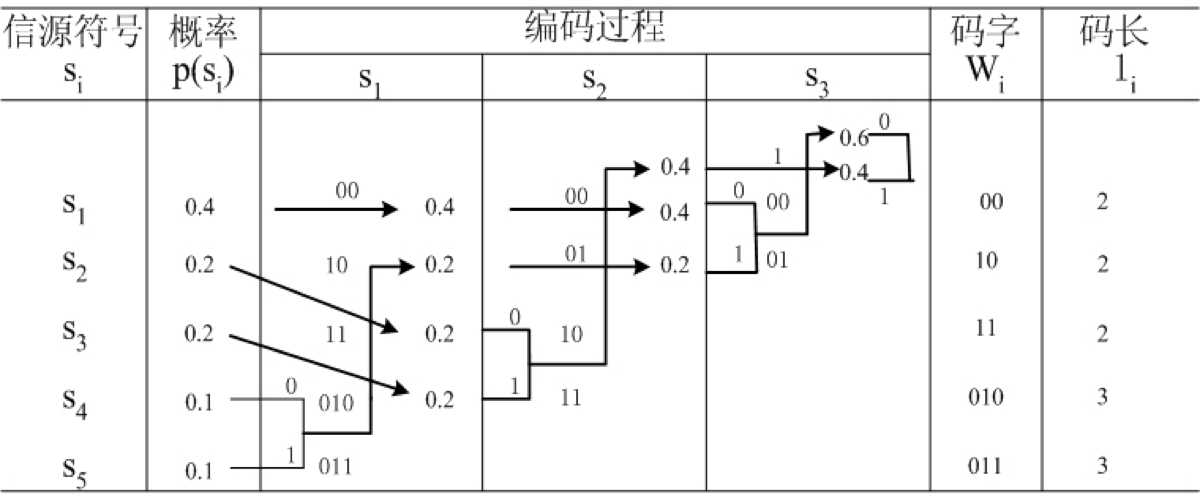
该霍夫曼的平均码长为
其编码效率为
从编码表可以看出,霍夫曼码是即时码。
2.3 不唯一性
- 每次对信源缩减时,赋予信源最后两个概率最小的符号,用 0 和 1 是可以任意的;
- 对信源进行缩减时,两个概率最小的符号合并后的概率与其它信源符号的概率相同时,这两者在缩减信源中进行概率排序时,其位置放置次序是可以任意的。
合并后的概率与其它信源符号的概率相同时,改变这两者在缩减信源中的排序,可以得到另一种霍夫曼编码,见下表:
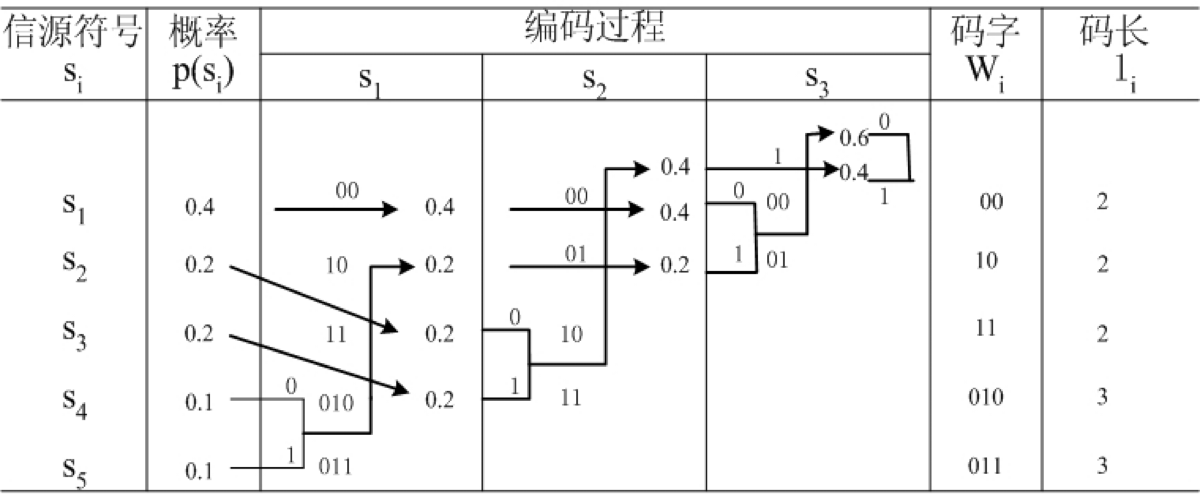
该霍夫曼码的平均码长
其编码效率
因此,编码效率与前一种霍夫曼码的效率相同。但后一种编码的码长方差
比第一种小,即码长变化小,简单,易实现。故在霍夫曼编码过程中,对缩减信源符号以概率重新排列时,应使合并符号尽量靠前,可使合并符号重复编码次数减少,使短码得到充分利用。
2.4
二进制霍夫曼码的编码方法可以很容易推广到
例:设有离散无记忆信源
码符号集
解:编码过程见下表,其中信源
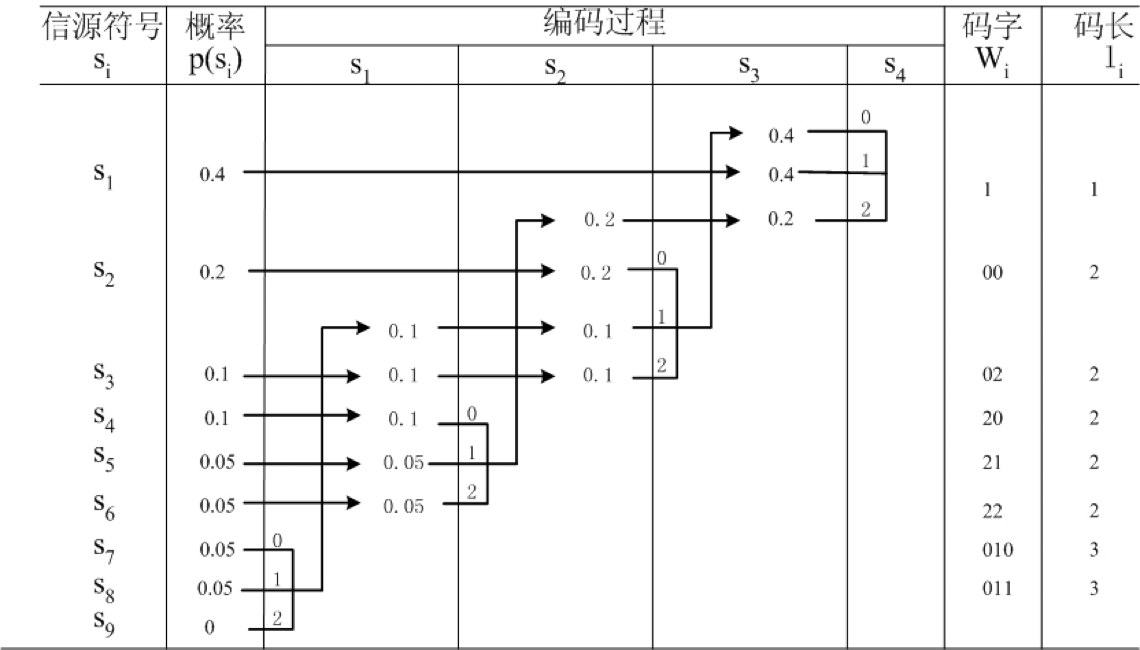
其平均码长为
2.5 总结
- 霍夫曼编码是最佳编码,用概率匹配方法进行信源的编码。它有两个明显特点:
- 霍夫曼编码的编码方法保证了概率大的符号对应于短码,概率小的符号对应于长码,充分利用了短码;
- 每次缩减信源的最后二个码字总是最后一位不同,从而保证了霍夫曼码是紧致即时码。
3. 费诺编码
3.1 过程
将信源发出的
将依次排列的信源符号依概率分为两大组,使两个组的概率和近于相同,并对各组赋予一个二进制代码符号“
将每一个大组的信源符号进一步再分成两组,使划分后的两个组的概率和近于相同,并又分别赋予两个组一个二进制符号“
3.2 例题
设有离散无记忆信源
进行费诺编码得到
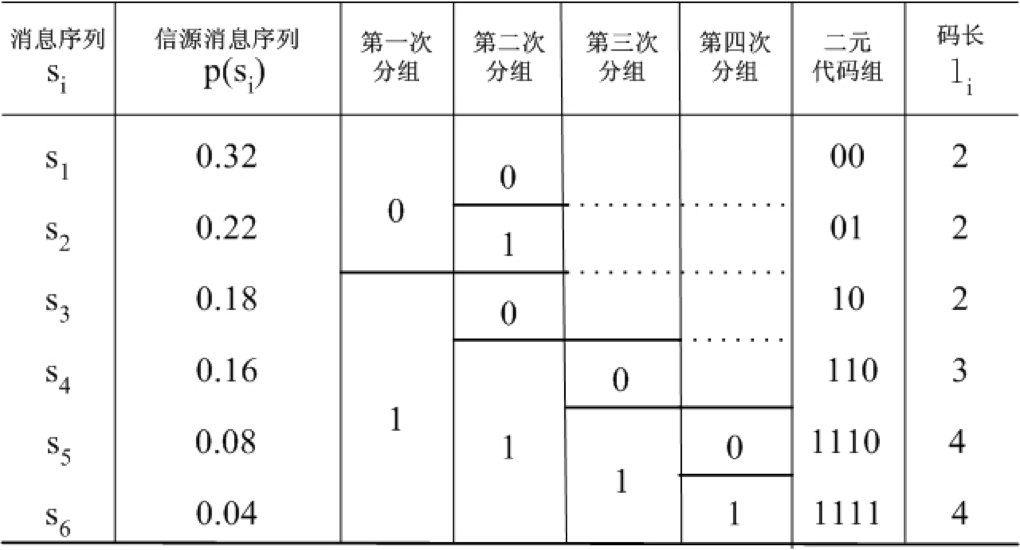
该费诺码的平均码长
信源熵
编码效率为
这里费诺码有较高的编码效率。费诺码比较适合于每次分组概率都很接近的信源,特别是对每次分组概率都相等的信源进行编码时,可达到理想的编码效率
4. 小结
介绍了几种变长码的编码方法。包括:香农编码、哈夫曼编码和费诺编码
变长码的缺点是高概率符号和低概率符号出现的不均匀,与信源符号恒速输出的矛盾,需要很大的缓存。信道可能无信息可送,或信息溢出而丢失。
变长码的另一缺点是差错的扩散。因为它采用异前置码来分解码字,一旦传送中出现误码,则某个码字的前置部分可能成为另一个码字,因而错译为另一个符号。需要采用差错控制。