一、信源的数学模型和分类
通信的根本问题是将信源的输出在接收端尽可能精确地复现出来,所以需要讨论如何描述信源的输出,即如何计算信源产生的信息量。
1. 信源的数学模型
信源发出消息,消息载荷信息,具有不确定性,所以可用随机变量或随机序列(随机过程)来描述信源输出的消息,或者说用概率空间来描述信源。
如上图,某信源可能发出的消息有
2. 信源的分类
2.1 离散信源与连续信源
根据信源输出的随机变量的取值,可以将信源分为离散信源和连续信源。
如果信源输出的随机变量取值于某一连续区间,为连续信号,消息的个数是无穷值,就叫做「连续信源」。比如人发出的语音信号,模拟的电信号等。
如果信源输出的随机变量取值于某一离散符号集合,消息在时间上的幅值均是离散的,就叫做「离散信源」。比如平面图像
2.2 单/多符号信源
信源的输出是单个消息符号,则称之为「单符号信源」,用一位离散或连续随机变量
信源输出的是多个消息符号,则称之为「多符号信源」,用
如自然语言信源就是把人类的语言作为信源,以汉字为例,就是随机地发出一串汉字序列。我们可以把这样信源输出的消息是为时间上或空间上离散的随机变量序列,即随机矢量。于是,信源的输出可用
值得一提的是,这里的连续离散强调的是「状态」,而并不关心时间上是否连续
二、单符号离散信源
1. 单符号离散信源的数学模型
设信源
则称
2. 信息量
2.1 自信息量
2.2 联合自信息量
二维联合集
式中
2.3 条件自信息量
联合集
由于每个随机事件的条件概率都处于 0~1 范围内,所以条件自信息量均为非负值。
2.4 几种自信息量之间的关系
自信息量、联合自信息量、条件自信息量都满足非负性和单调递减性三者都是随机变量,其值随着变量
自信息量
3. 信源熵
自信息量
对于整个信源来说,它的信息测度该如何表示?先举一个直观的例子,有一个布袋,装有 100 个手感一样的球,但颜色不同,每种颜色球的数量也不同。随意从中拿出一球,猜测球的颜色。猜测的难度越高,表明布袋的不确定度越高。
- 90 个红球,10 个白球 ---容易猜测
- 50 个红球,50 个白球---较难猜测
- 红、白、黑、黄球各 25 个---更难猜测
容易看出:
- 信源的不确定程度与信源概率空间的状态数及其概率分布有关;
- 如果信源概率空间的状态数确定,概率分布为等概时,不确定程度最大;
- 等概时,不确定程度与信源概率空间的可能状态数(或相应的概率)有关,状态数越多(或相应的概率越小),不确定程度就越大。
信源的不确定程度通常可以用信源概率空间的概率分布来描述,通常记为
3.1 信息熵
定义
集
定义为该集的「平均自信息量」。集
信源熵与平均自信息量数值相等,含义不同
- 信源熵表征信源的平均不确定度;
- 平均自信息量是消除信源不确定度所需要的信息的度量;
信源熵
- 表示信源输出后,每个离散消息所提供的平均信息量;
- 表示信源输出前,信源的平均不确定度;
- 反映了变量
例题
有 12 枚硬币(币值相同),其中有一枚为假币,只知道假币的重量和真币不同,但不知是轻还是重。现采用天平(无砝码)比较左右轻重的方法来找出这枚硬币。问至少要称几次?怎么称?
设假币为
而每次称重可以获得的信息量
因此需要的次数为
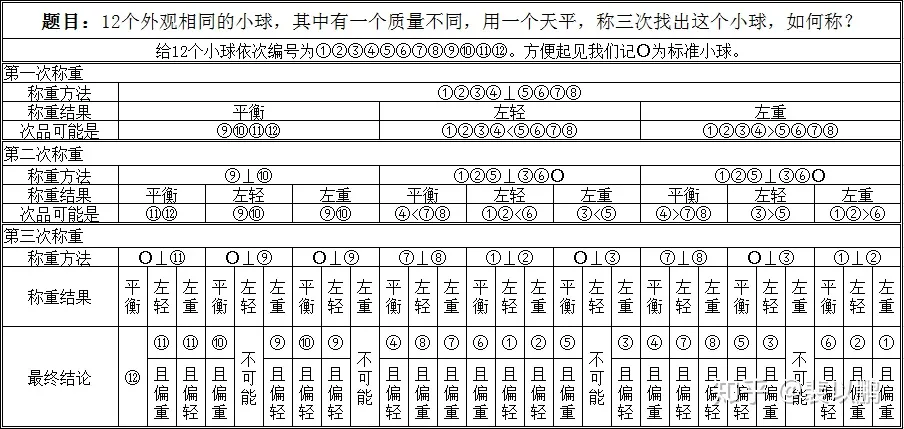
3.2 条件熵
联合集
上式称为联合集
式中取和的范围包括
该式表示前面一个消息符号给定时,
因此,条件熵的定义式为
3.3 联合熵
联合集
根据联合自信息量的定义,联合熵又可定义为
联合熵又可称为「共熵」。
4. 信源熵的性质和定理
4.1 数学特征
随机变量集
根据此式,再由概率的完备性,
4.2 对称性
当概率矢量
4.3 非负性
其中等号成立的充要条件是当且仅当对某
即,信源虽然有不同的输出符号,但它只有一个符号几乎必然出现,而其他符号几乎都不可能出现,那么,这个信源是一个确知信源,其信源熵等于零。这种非负性对于离散信源的熵是正确的,但是对于连续信源来说,该性质不存在。
4.4 扩展性
含义:若集合
证明
由于极限速率的问题
4.5 可加性
如果有两个随机变量
当二维随机变量
证明
4.6 最大熵定理
其中
证明
由不等式
因此
当且仅当
4.7 确定性
集合
4.8 极值性
对任意两个消息数相同的信源
证明
故不等式成立
4.9 上凸性
前置知识——凸函数
凸函数
设
则称
则称
则称
上凸性
现在回到熵函数的性质。对于一个熵函数,
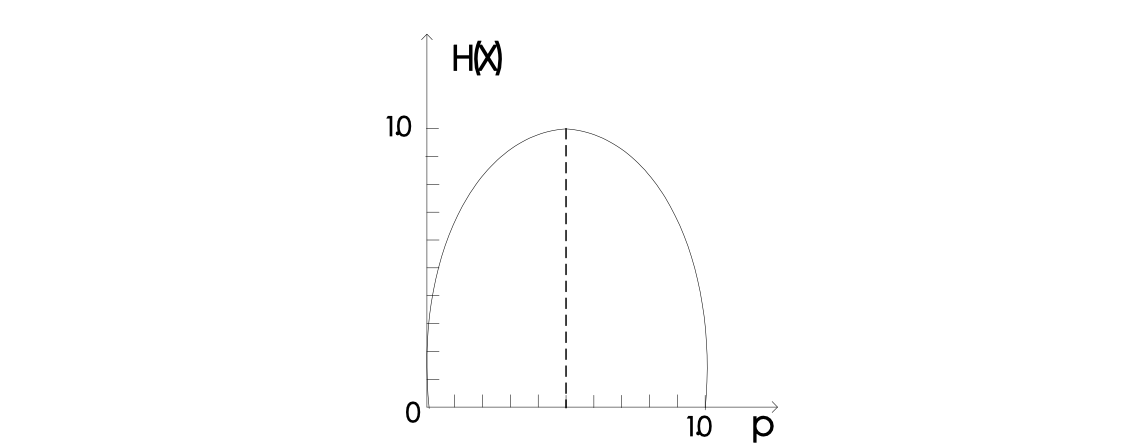
5. 熵之间的关系
5.1 联合熵与信息熵、条件熵的关系
由此可得推论
如果集
还可以将此性质推广到多个随机变量构成的概率空间之间的关系,设有
若
证明:
根据概率论的相关公式
同样可以推广到
5.2 共熵与信息熵的关系
当集合
该性质可以推广到
5.3 条件熵与信源熵的关系
条件熵小于信源熵,即
证明:
由极值性
当且仅当 $p(x_i|y_i)=p(x_i),i=0,1,2,\cdots $,等式成立
例题
设一系统的输入符号集
求联合集
解:
根据
和条件概率公式
每一行相加,得到
由此可以求出
根据信息熵的公式
同理
同理
三、多符号离散平稳信源
1.
1.1 一维离散信源
最简单的离散信源可以用一维离散随机变量描述
且
若
信源模型为
这就是最简单的离散信源,它只有
1.2 离散无记忆二进制信源的二次扩展信源
将两个最简单信源

二次扩展信源的输出消息是符号序列,分组发出,每两个二进制符号构成一组,其数学模型为
其中
其中
1.3 离散无记忆二进制信源的三次扩展信源
若在加上一个信源
其中
其中
1.4 离散无记忆二进制信源的
根据二次和三次的定义,我们顺理成章可以将扩展信源扩展到
其中
其中
2.
给出
2.1 定理
离散无记忆信源
单个信源的熵是容易计算的。根据此定理,我们就可以用单符号信源的熵计算其拓展信源的熵。此定理告诉我们,离散无记忆信源的
2.2 证明
由
因为
先考察第一项,注意到
同样计算上式中的其余
例题
设有一离散无记忆信源
求信源
解:
因为原始信源
用表格表示为
| 信源符号 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 符号系列 | |||||||||
| 概率 |
计算得原始信源熵
因此根据定理,直接可以得到
3. 离散平稳信源
比较重点
3.1 一维平稳信源
对于随机变量序列
则称这种信源为「一维平稳信源」。一维平稳信源无论在什么时刻均以
3.2 二维平稳信源
对于一个一维平稳信源,若联合概率分布
其中
3.3
如果
其中
则称具有这样性质的信源为「
3.4 离散平稳信源
如果各维联合概率分布均与时间起点无关,即对两个不同的时刻
这种各维联合概率均与时间起点无关的完全平稳信源称为「离散平稳信源」
3.4 离散平稳有记忆信源
离散平稳信源一般是有记忆信源。发出的各个符号之间具有统计关联关系。统计关联性可用两种方式表示:
- 用信源发出的一个符号序列的整体概率,即
- 用信源发出符号序列中各个符号之间的条件概率来反映记忆特征,这是发出符号序列的马尔可夫信源。这种反映方式比联合概率要简单一些。
4. 离散平稳信源的信息熵
4.1 定义
以最简单的二维平稳信源为例,它是
由熵的定义
称上式为平稳信源的「联合熵」
4.2 熵的可加性
一般信源发出的符号序列中,前后符号之间总是存在着依赖关系。定理指出,两个有相互依赖关系的随机变量
此时,将信息熵的关系式
称为「熵的强可加性」。当前后序列没有依赖关系时,
4.3 二维平稳信源与二次扩展信源
当
与离散无记忆信源的二次扩展信源的情况相同。所以离散无记忆信源的二次扩展信源的特例。由于条件熵小于无条件熵,所以
说明二维离散平稳有记忆信源的熵小于等于二维离散平稳无记忆信源的熵。告诉我们在编码时尽量避免记忆性,才能编更大的信息量。
- 对于二维离散平稳无记忆信源
- 对于二维离散平稳有记忆信源,由于
例题
设二维离散信源
求二次扩展信源的联合熵
解:原始信源的熵为
由表中条件概率可知条件熵为
条件熵
信源
平均到
显然它小于信源
5. 离散平稳信源的极限熵
记平稳有记忆
由熵的性质可知
5.1 性质
对于这一系列条件熵,我们有性质:条件熵随着
根据平稳性质可以证明。
5.2 平均符号熵
若信源输出
为信源的「平均符号熵」。它表示信源输出
5.3 极限熵
定义
若信源输出
称为信源的「极限熵」。多符号离散平稳信源实际上就是信源在不断地发出符号,符号之间的统计关联关系也并不仅限于长度
极限熵存在定理
对任意平稳离散信源,若有
证明略。
6. 马尔可夫信源
有记忆信源在任一时刻发出符号的概率通常仅与前面的若干个符号有关,与更前面的符号无关,因此我们可以认为信源在某一时刻发出的符号与信源的状态有关。
设信源状态空间为
记信源输出的随机信号序列为
信源所处的状态序列为
6.1 定义
若信源输出的符号序列和状态序列满足下述条件
- 某一时刻
- 信源的状态只由当前的输出符号和前一时刻信源状态唯一确定,即
则称此信源为「马尔可夫信源」
6.2 一步转移概率
马尔可夫信源输出的符号序列
其中
可通过引入状态转移概率来转化为马尔可夫链。即令
其状态
通常我们用马尔可夫链的状态转移图来描述马尔可夫信源。
6.3
当时间足够长时,遍历的
即
由前面的分析可知,齐次、遍历的马尔可夫链
此公式要求记住。因此可以由此公式求得极限熵
其中
及条件
这就是在马尔可夫链下,极限熵的求法
例题
设有一个二进制二阶马尔可夫信源,信源符号集为
试求其平稳分布和极限熵
解:
令
由平稳可得方程
即
推出
即
7. 信源冗余度
7.1 相关性和剩余度
随着条件增多,熵值逐渐减小到极限熵。当离散平稳信源输出符号为等概率分布时熵最大,即平均自信息量
每发送一个符号,都能传送
7.2 剩余度
为了衡量信源的相关性程度,引入剩余度概念。定义
为信源的「剩余度」,其中
为信源熵的「相对率」,因此有
四、连续信源
实际应用:信源的输出往往是时间的连续函数,如语音信号、电视图像等。由于它们的取值既是连续的又是随机的,称为连续信源,且信源输出的消息可以用随机过程描述。
连续信源的数学描述:对于某一连续信源
1. 连续信源的数学模型
若给定
简单连续信源的模型可写为
假设
根据积分中值定理可以得到,可以找到一点
离散化后,对连续信源的熵,就可以用此离散信源的熵来近似。
求极限
由于
因此原式化为
其中
前一项为有限的函数,但后一项是负无穷,等价于加上了一个正无穷的值。连续信源的熵等于无穷大!而在计算机里面我们无法处理无穷大量,那该如何处理呢?
我们规定,对于连续信源
连续信源的熵与离散信源的熵具有相同的形式,但其意义不相同。连续信源熵与离散信源熵相比,去掉了一个无穷项,这么做的合理性在哪?
这是因为实际应用中常常关心的是熵之间的差值,无穷项可相互抵消,故这样定义连续信源的熵不会影响讨论所关心的交互信息量、信息容量和率失真函数。
需要强调的是连续信源熵的值只是熵的相对值,不是绝对值,而离散信源熵的值是绝对值。
信息论研究的是信息是如何让不确定性减少的过程——香农
因此这么做是有其实际意义的。因为这两个无穷项是可以互相抵消的。
2. 几种特殊连续信源的熵
2.1 均匀分布
均匀分布随机变量的概率密度为
求其熵
解:
根据定义
这就是均匀分布的熵值。但我们发现,当
2.2 高斯分布
求均值为
根据连续熵定义,为了计算方便,我们这里用
调整负号顺序
注意到归一性
因此高斯分布的熵值为
我们发现,高斯分布的熵值只与方差有关,与均值无关。 可以理解为,正态分布的直流功率不影响其熵值,因为直流不携带信息量。我们把这个叫做「交变功率」,只有交变功率才能提供信息量。
显然,高斯分布的熵值也是可正可负的
2.3 连续熵的性质及最大连续熵定理
对于离散信源,当所有消息独立等概率分布时,其熵值最大。而在连续信源情况下,如果没有条件限制就没有最大熵。在不同限制条件下,信源的最大熵也不同。
对于连续信源,当存在最大熵值时,其概率密度函数
为最大条件下,求解
连续信源的最大熵定理
在具体应用中,仅讨论连续信源的两种情况:
- 一是信源输出的幅度受限;
- 二是信源输出的平均功率受限。
根据这两种情况,有两条定理
定理一
在输入信号幅度受限的条件下,服从均匀分布的随机变量
证明
幅度受限,即
为了求出这个最大值,我们引入拉格朗日算子,这里的
为了求出极值,要求导数为零,我们令
得出
即得出
根据归一化条件
由此得到
时,即均匀分布时连续熵取得最大值。这与离散情况下的最大熵定理联系起来了。
定理二
在平均功率受限的条件下,服从均值为
证明
平均功率受限,即是在条件
引入两个拉格朗日算子
对后两项稍做变换
利用基本不等式
积分式为零,对应积分号里面也必须为零。由此可以得到
又根据归一化条件及
因此当
4. 熵功率
由于高斯信源具有最大熵
对于其他分布的信源,当平均功率
为该信源的「熵功率」,其中
这是因为其他功率很多是无用功。只有高斯全部用在发射信息上了。
5. 联合熵和条件熵
设有两个随机变量
为
为
6. 各种熵值的关系
由于连续信源是相对熵,不具有非负性和极值性。存在如下关系式
当信源
并且存在
当信源彼此独立时,等号成立。