一、基本概念
重点掌握第一章,关于求解不考,离散连续都不考,编码定理放在编码讲
无论无噪信道还是有噪信道,只要信息传输率
反之,如果
传送每秒 25 帧的图像就能满足人类通过视觉感知信息的要求,而不必占用更大的信息传输率。人类的听觉对大多数人只能听到几千赫兹到十几千赫兹,对于经过专业训练的音乐家,一般也不过听到
因此,实际应用要求在保证一定质量前提下,在信宿近似地再现信源输出的信息,或者说在保真度准则下允许信源输出存在一定的失真。
本章需要解决的问题:对于给定的信源,即给定信源熵
信息率失真理论是研究信源熵的压缩问题,采用研究信道的方法,即在数学上讲信源熵压缩看成通过一个信道,寻找在保真度准则下的最小的平均互信息。在这里,我们把压缩算法看成是抽象信道。
信息率失真理论是信号量化,模数转换、频带压缩和数据压缩的理论基础,在图像处理、数字通信等领域得到广泛应用。
1. 失真函数
1.1 定义
设离散信源
经信道传输后的输出序列为
用一个非负的函数
称此矩阵为「失真矩阵」。假定离散矢量信源
其中第
其中第
或
矢量失真函数矩阵共有
例题
例1
设信源符号序列为
求失真矩阵
例 2
此时的失真矩阵为
特点:当
例 3
平方误差失真函数
特点:一般用于表示由幅度变化引起的失真,幅度失真越大,引起的错误越严重。
例 4
假定离散矢量信源
解:
由矢量失真函数的定义得
由此可以得到
2. 平均失真度
假定离散信源为
经信道传输后的输出序列为
2.1 定义
由于
平均失真
其中第
则平均失真度为
其中
3. 信息率失真函数
3.1
若预先规定的限定失真度为
对于离散无记忆信道,相应有
3.2 信息率失真函数
在
注意,
其中
信息率失真函数的意义:对于给定的信源,在满足保真度准则
4. 信息率失真函数的性质
4.1 定义域
由于平均失真度
当
显然,当失真矩阵每一行都有零元素时,可达到零。当失真矩阵每一行都没有零元素时,可用坐标变换使其每一行都有零元素。故一般可认为
那么应该如何求出
由于
所以有
由于信源概率分布
例
二元信源
给出失真度矩阵
求
解:
我们先分别算出
由此得到
此时
失真矩阵每行都有零元素,得
最重要的部分已经讲完了
4.2 下凸性
假定
令
可以证明
这表明
4.3 递减性
有
4.4 一般曲线
由上面的性质,我们可以得到离散信源率失真函数
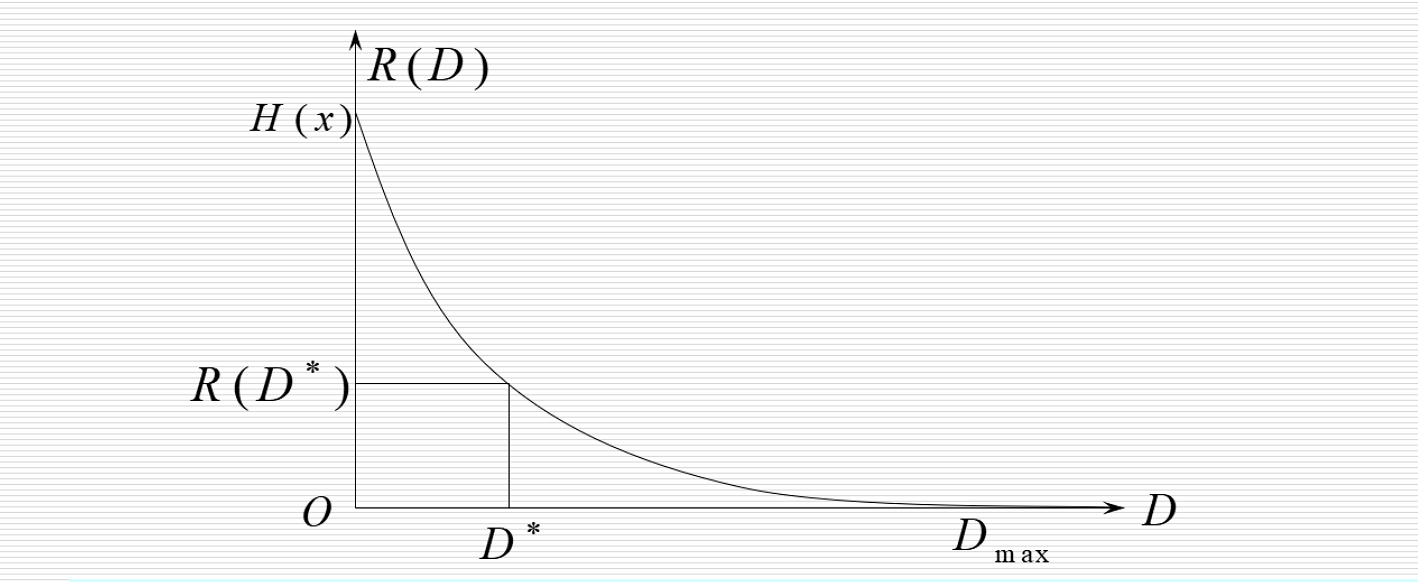
5. 限失真信源编码定理
不详细说,直接给出一个实际性
设一离散平稳无记忆信源的输出随机变量序列为
只要信源序列长度
即:译码平均失真大于允许失真。称此定理为「限失真信源编码定理」或「香农第三定理」。证明略。该定理可推广到连续平稳无记忆信源的情况。
6. 对信息编码定理的统一理解
定长信源无失真编码定理:
变长信源无失真编码定理(香农第一定理):
保真度准则下的信源编码定理(香农第三定理):
从编码信息率的角度,当
以下不考
二、离散信源的信息率失真函数
这部分不要求,笔记就不做了
对于离散信源来说,求信息率失真函数
一致信源的概率分布
一般情况下难于求得闭式解,常采用参量表示法,或采用迭代算法求解。
1.
设离散信源的输入序列为
输出序列为
字符传输的失真函数为
信息率失真函数
求
对于一个信源来说,不均匀的时候时容易压缩的。
2. 二元及等概离散信源的信息率失真函数
2.1 二元离散信源
2.2 等概离散信源
上式中第一项是等概率信源的熵,即无失真传送信源所必须的信息率,后两项则是由于容忍一定失真可以压缩的信息率。
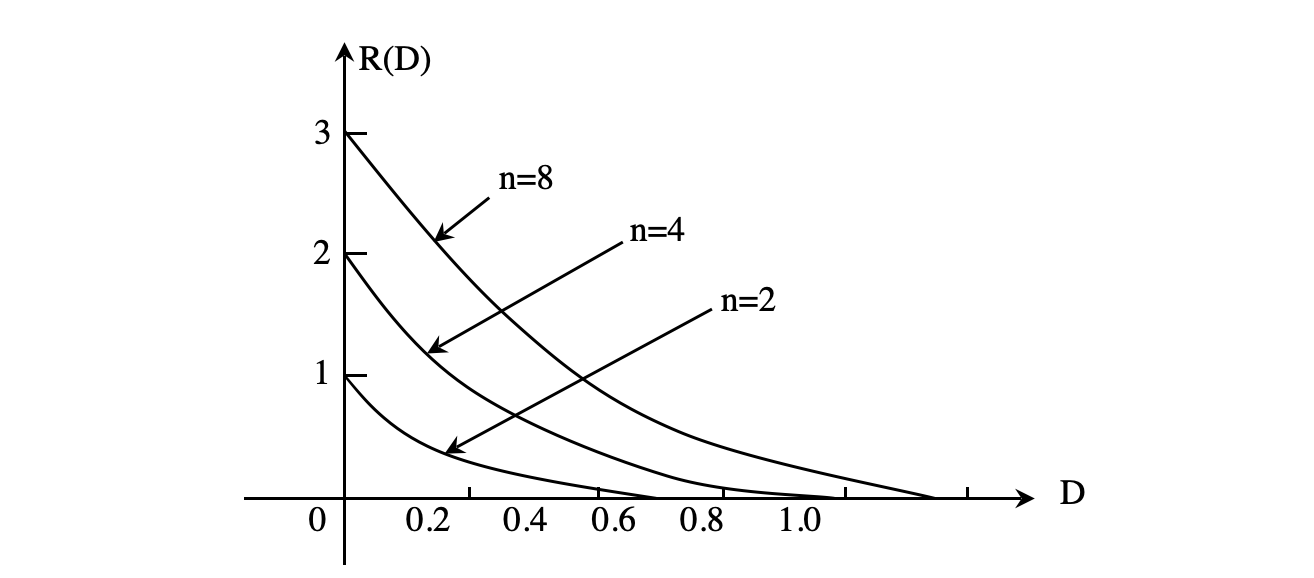
对于同一失真度D,n越大,R(D)越大,压缩率(可能性)越小;反之,
对于同一失真度D,n越小,R(D)越小,压缩率(可能性)越大。
当n=2,α=1时,R(D)=H(p)-H(D)=lnn -H(D)
如果信源的符号数目为n,那么在满足保真度准则下,符号数越多,信源的可压缩性越小;反之,符号数越少,信源的可压缩性越大。
只需要记住这两个结论,不需要掌握计算
不同
3. 信息率失真函数的性质
4. 保真度准则下的信源编码定理
三、连续信源的信息率失真函数
一般情况下,信息在传输过程中必然会存在一定的噪声和干扰,使得信源的消息在传输过程中存在一定的误差和失真。对于连续信源,在传输过程中总会有波形失真,连续信源的信息率失真理论就是在一定意义上定量分析信号的失真程度。
本节主要讨论连续信源的信息率失真函数,连续信源的率失真理论与离散信源情况基本相同。
1. 连续信源信息率失真函数的参量表达式
1.1 平均失真度
定义: 设连续信源(随机变量)
式中
1.2 信息率失真函数
设所有试验信道的集合为
式中
2. 高斯信源的信息率失真函数
设高斯信源
有两种方法可求(略):
- 应用拉格朗日算子,与离散的算法类似。
- 用反向信道。
其结果是
所有的连续信源都有这种特性。
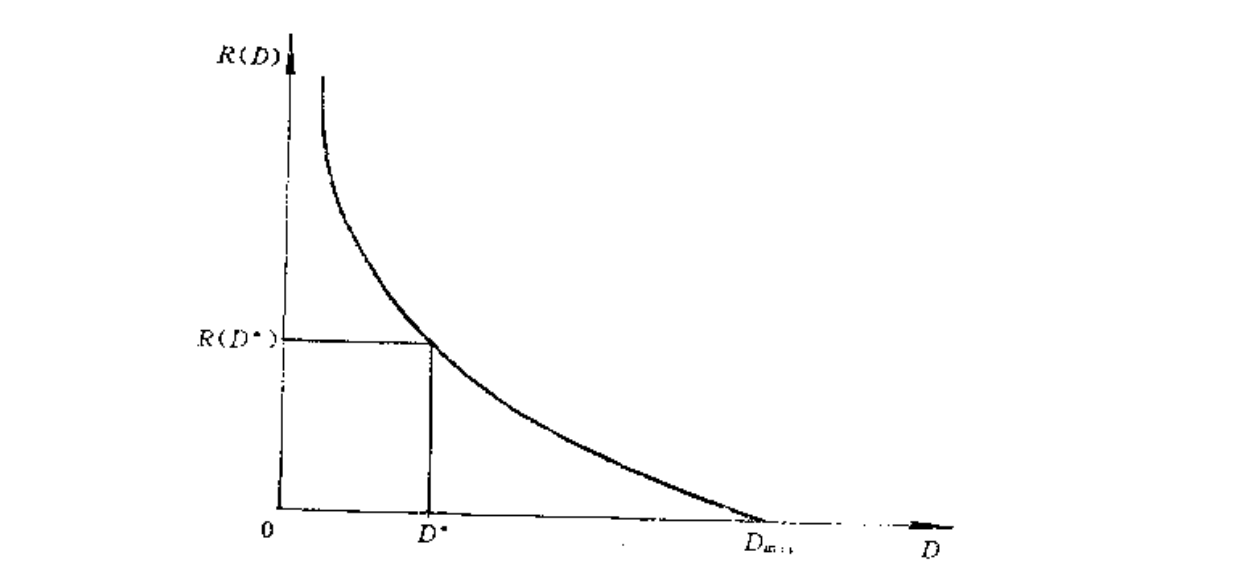
3. 信息率失真函数与信息价值
直接不讲了
4. 信道容量与信息率失真函数的比较
4.1 信道容量
平均互信息的上凸性。固定信道,求解
信道容量
研究信道容量是为了解决通信的可靠性问题,是信息传输的理论基础,通过信道编码增加信息的冗余度来实现。
4.2 信息率失真函数
平均互信息的下凸性。固定信源概率分布,求解信道的情况。
信息率失真函数一旦求出后,就只与信源概率分布(密度)有关,反映信源特性,与信道特性无关。
信息率失真函数则是为了解决通信的有效性问题,是信源压缩的理论基础,通过信源编码减少信息的冗余度来实现。