一、半导体
从导电性来说,电学上的材料可以分为
- 导体(Conductor):导电性很强
- 绝缘体(Insulator):导电性很差
- 半导体(Semiconductor):导电性介于两者之间
模拟电路这门课程本质上就是在研究一系列由半导体制成的元件组成的电路。
1. 半导体的微观机理
半导体的原子结构
构成三种材料原子结构不同,决定了他们的导电性不同。
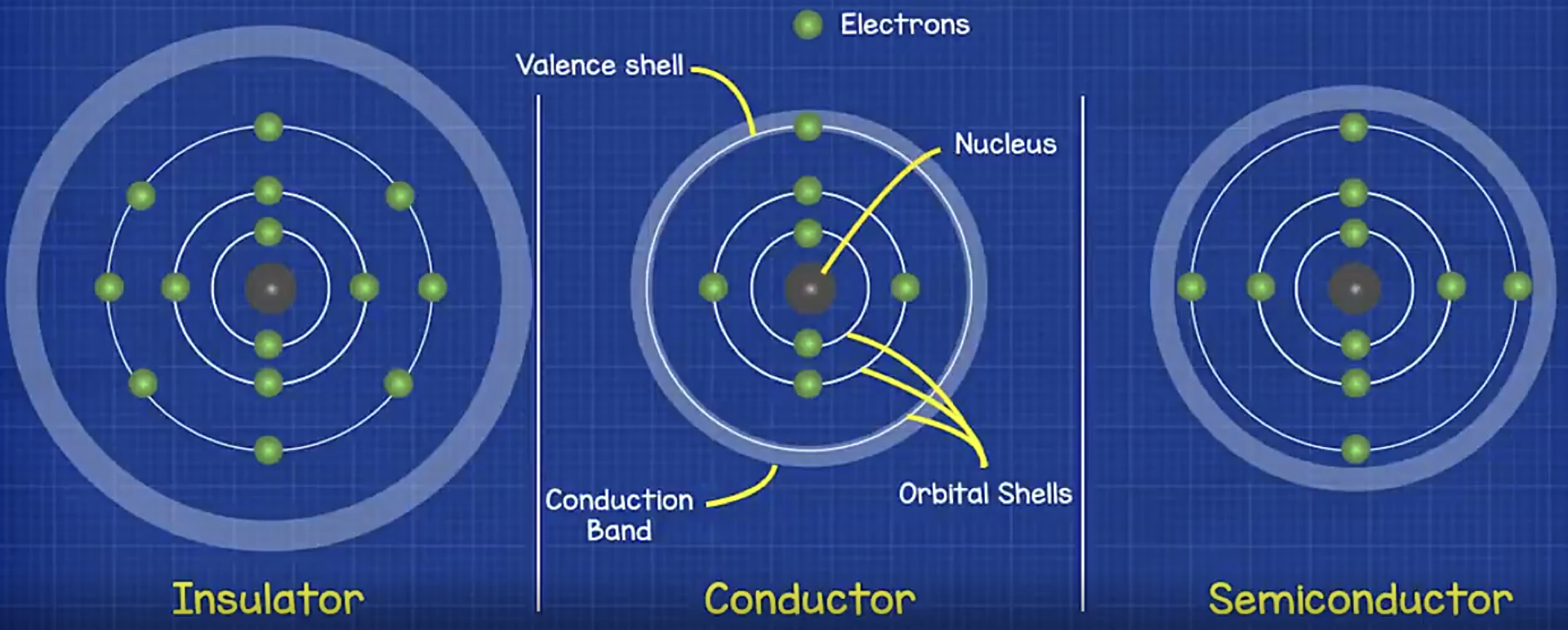
对于绝缘体来说,各电子轨道处于全满状态的稳定状态,很难得失电子,因此电子在原子间难以传递。
对于导体来说,最外层轨道的电子很少,通常只有一两个。最外层的电子在外电场作用下很容易失去,在材料内部形成电流。
而半导体的情况介于两者之间。最外层处于半满状态。
本征半导体
由同一种原子晶体组成的半导体材料称为「本征半导体」(Intrinsic semiconductor),如硅晶体,锗晶体等。
当温度趋于绝对零度时,本征半导体表现出绝缘体的性质。但当温度上升时,在热效应作用下,少量最外层电子成为「自由电子」(Free electron),在原处留下「空穴」(Holes)。空穴和自由电子是一对相对的概念。对于硅原子来说,其最外层有四个电子,若失去一个电子,则其相对于普通的硅原子来说呈正电性,可以认为是这个丢失的电子在原处留下的空穴而“导致”的正电性。因此我们认为,自由电子呈负电性,空穴呈正电性。对于半导体材料来说,这两者都是可以作为电流的载流子。
纯净的半导体中,自由电子和空穴的数量大致相等,且两者数量都非常少,因此本征半导体的导电性非常弱。
杂质半导体
为了提高半导体的导电性,可以在纯净的半导体中掺入其他类型的原子,如三价和五价元素,称掺有杂质的本征半导体为「杂质半导体」。根据掺杂的原子不同可以分为「N 型(n-type)半导体」和「P 型(p-type)半导体」。N 型半导体表示掺杂的原子比主要的原子多出一个电子,呈负电性;P 型则表示少一个电子,呈正电性。掺杂可以显著提升半导体材料的导电性(
对于 N 型半导体而言,半导体内自由电子较多而空穴较少,因此两种载流子中起主要作用的是自由电子,而对于 P 型半导体,结论相反。
我们称在半导体材料的两种载流子,即空穴和电子之中占大多数,导电中起主要作用的载流子为多数载流子(Majority carrier),或「多子」;与之对应的较少的称为少数载流子(Minority carrier),或「少子」
多子的浓度主要由掺杂浓度决定,受温度的影响较小,而少子浓度主要由温度决定
载流子运动
半导体中的载流子存在两种运动方式
- 载流子在外加电场的作用下的移动叫做「漂移」(Drift)
- 载流子从高浓度区域向低浓度区域的移动叫做「扩散」(Diffusion)
2. PN 结
当 N 型半导体和 P 型半导体放置在一起时,N 型半导体的自由电子在浓度差的作用下向 P 型半导体发生扩散,同理,P 型半导体的空穴也向 N 型半导体发生扩散。
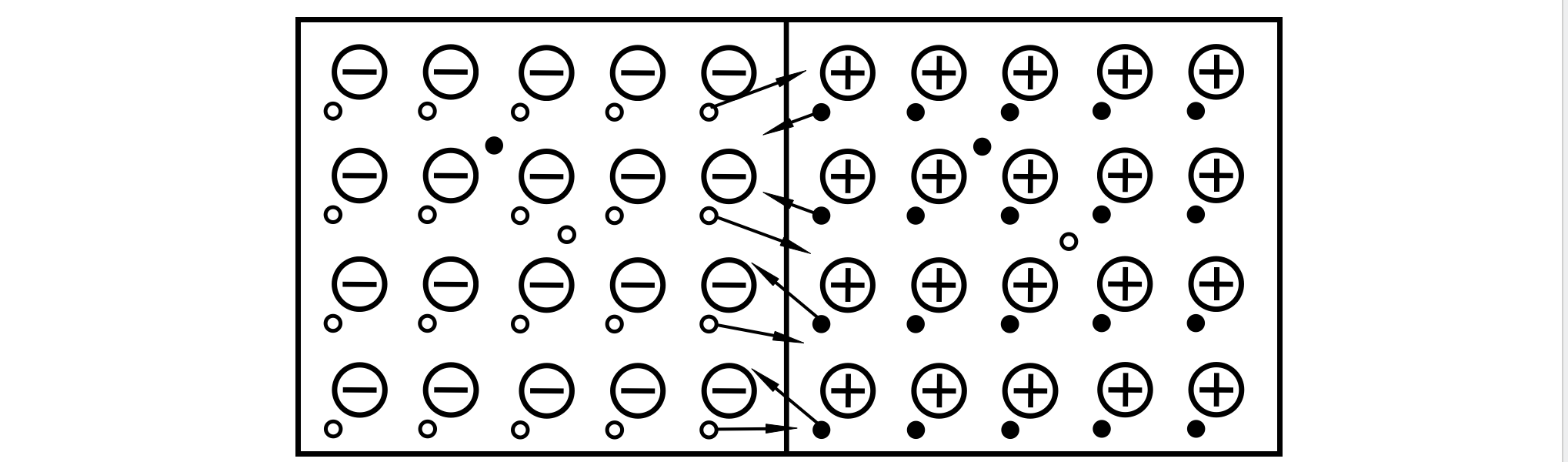
在扩散作用下,N 型半导体靠近交界面处的原子相对于原来的 N 型半导体呈电正性,而 P 型半导体的交界面靠近交界面处的原子呈电负性。从而在两种半导体之间形成了一个电性略有不同的区域,称之为耗尽区(depletion region)
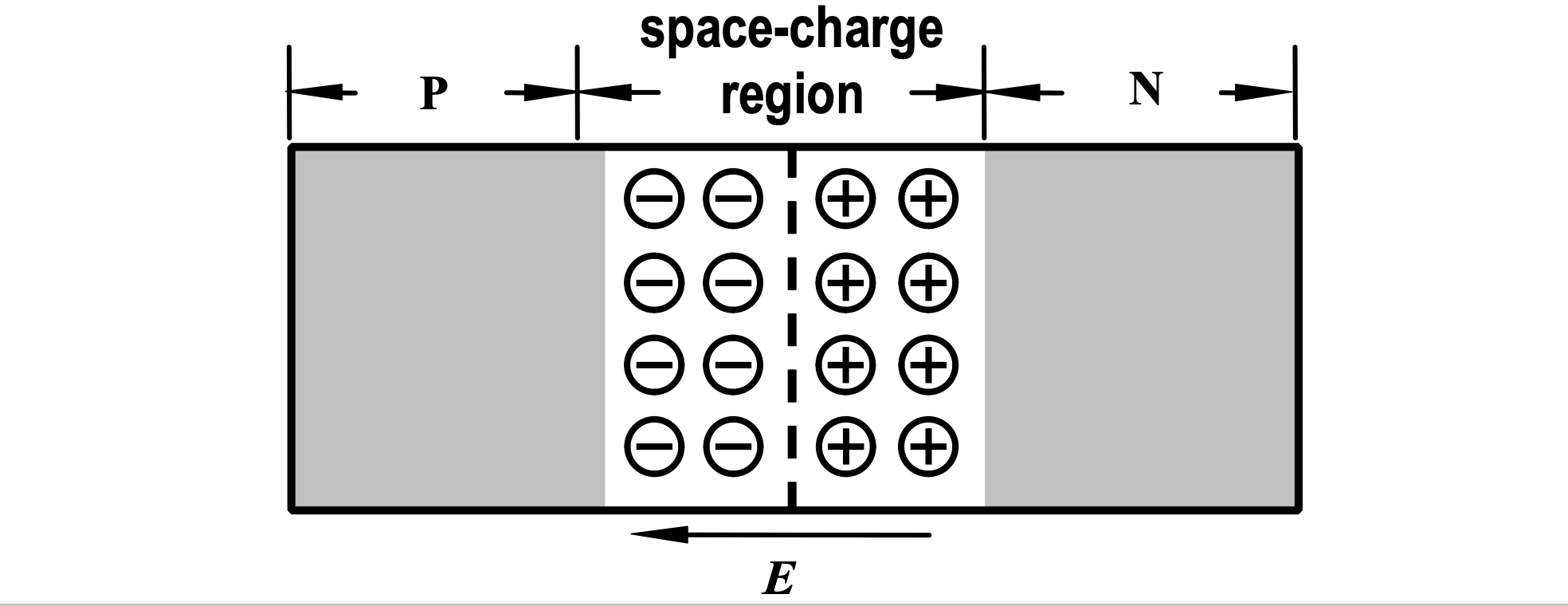
此耗尽区存在一个相对电场,场强方向从 N 型半导体指向 P 型半导体,在此电场的作用下,载流子扩散运动的同时还存在反方向的漂移运动,在两者的平衡作用下,形成了一个相对稳定的平衡区域,称此区域为「PN 结」(The PN Junction),在此状态下,来自 P 型半导体的空穴受 PN 结电场的作用,无法顺利到达 N 型半导体,反之,自由电子也无法顺利到达 P 型半导体,即 PN 结能阻碍载流子通过。
PN 结正偏
若对 P 型半导体正电压,对 N 型半导体通负电压,则称此 PN 结处于「正偏」(forward-biased)状态。
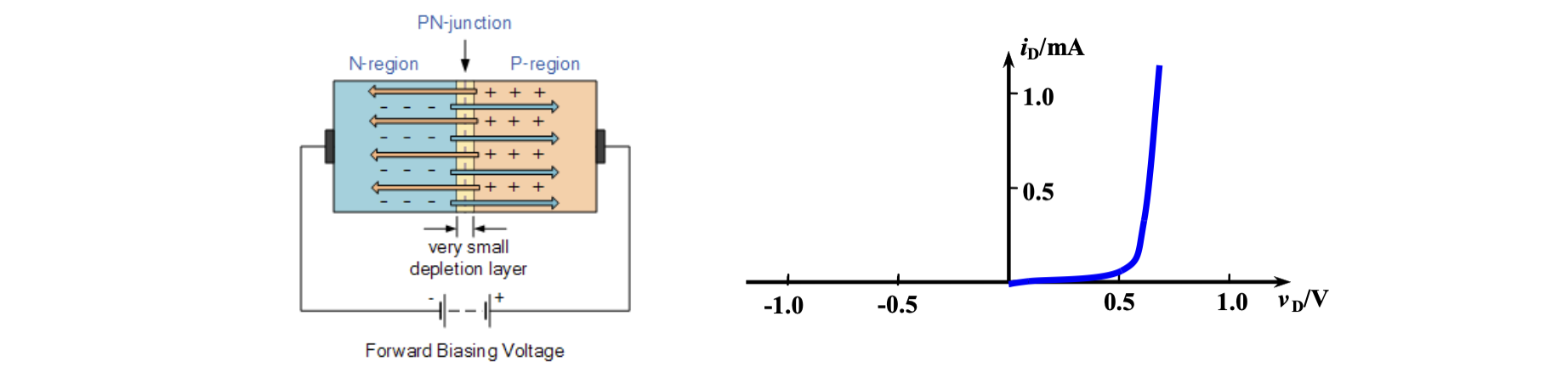
正偏时,在外加电场作用下,来自 P 处的正电荷中和 PN 结左侧的负电荷,而来自 N 处的负电荷中和 PN 结右侧的正电荷,导致 PN 结变薄,对载流子阻碍作用减小,从宏观上来看,就是此半导体的电阻减小
PN 结反偏
若对 P 型半导体负电压,对 N 型半导体通正电压,则称此 PN 结处于「反偏」(reverse-biased)状态。
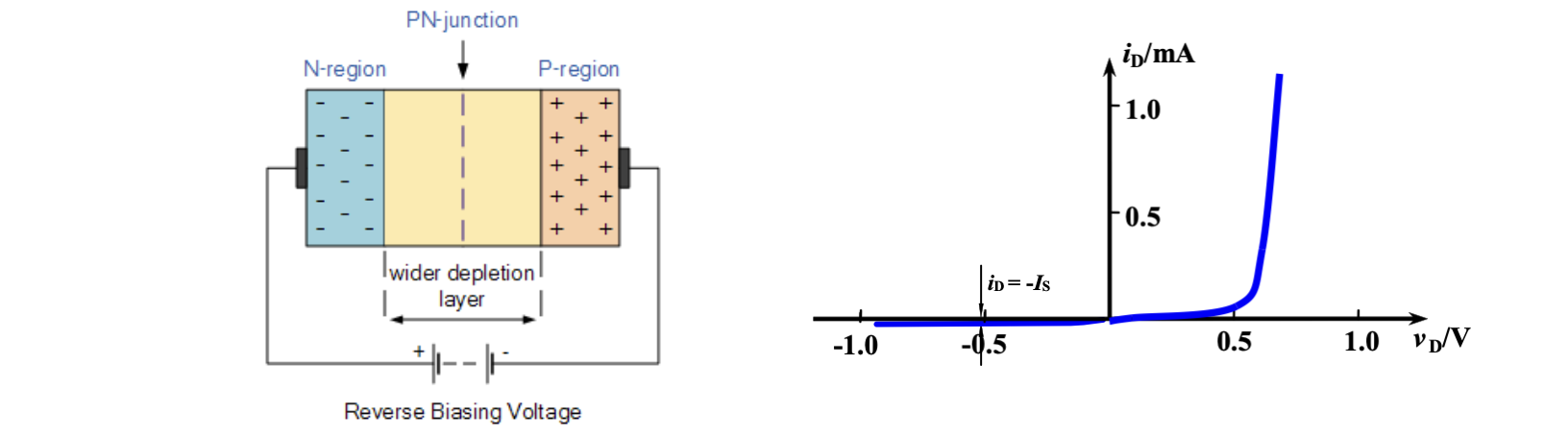
反偏时,在外加电场作用下,来自 P 处的负电荷结合 PN 结左侧的负电荷,而来自 N 处的正电荷结合 PN 结右侧的正电荷,导致 PN 结变厚,对载流子阻碍作用减大,从宏观上来看,就是此半导体的电阻增大,多子无法正常通过,但少部分少子在 PN 结强大的浓度差作用下可以少量通过,形成了极小的电流。此电流被称为「反向饱和电流」(reverse saturation current)或「漏电流」(leakage current)
当反向电压增加到一定程度时,电流会急剧增加。称这个转折点为「击穿电压」(Breakdown voltage)。
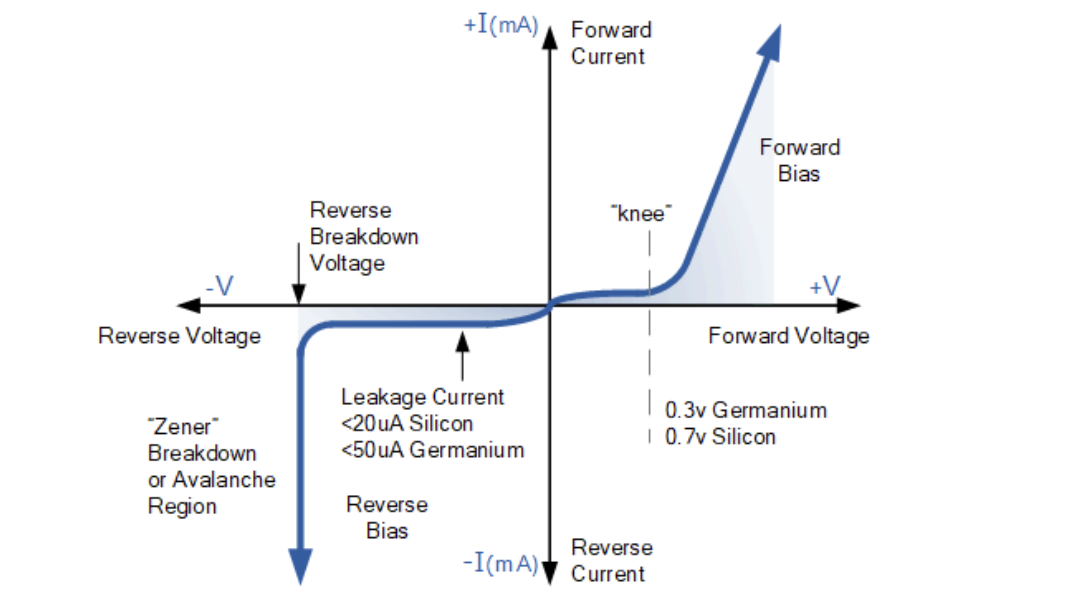
理想特性曲线
二极管的电流随电压呈指数型增加,用公式可以表示为
其中
由于 PN 结在正偏和反偏所具有的导电性不同,根据此原理就可以制作正反电阻不同的半导体元件——「二极管」(Diode)。
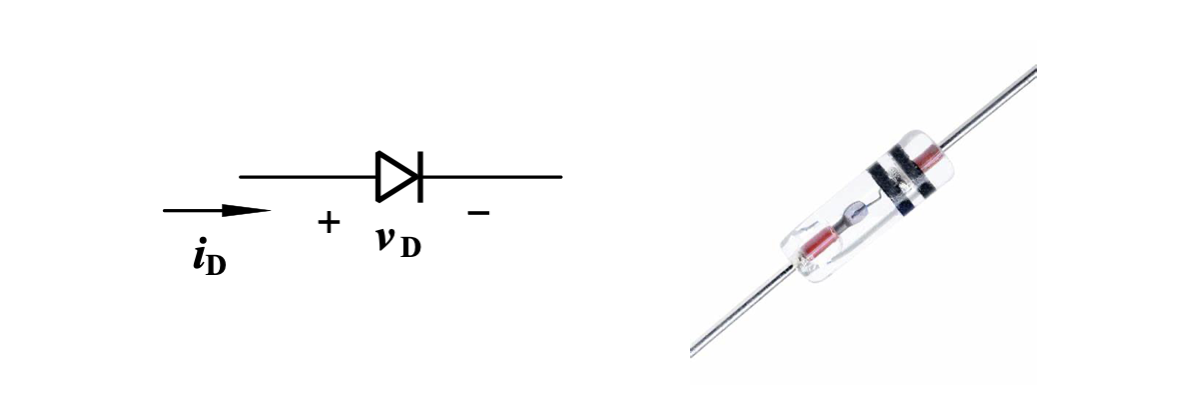
上图为二极管的电路符号,其中三角形的指向为其正偏方向,从正极指向负极。
温度效应
上文提到,二极管的特性曲线满足
但注意到,
电容效应(不要求)
其中,
反向击穿
当对二极管施加反向电压时,随着反向电压增大,反向电流急剧增大的现象称为反向击穿(Reverse breakdown),可以分为雪崩击穿(Avalanche breakdown)和齐纳击穿(Zener breakdown)两种
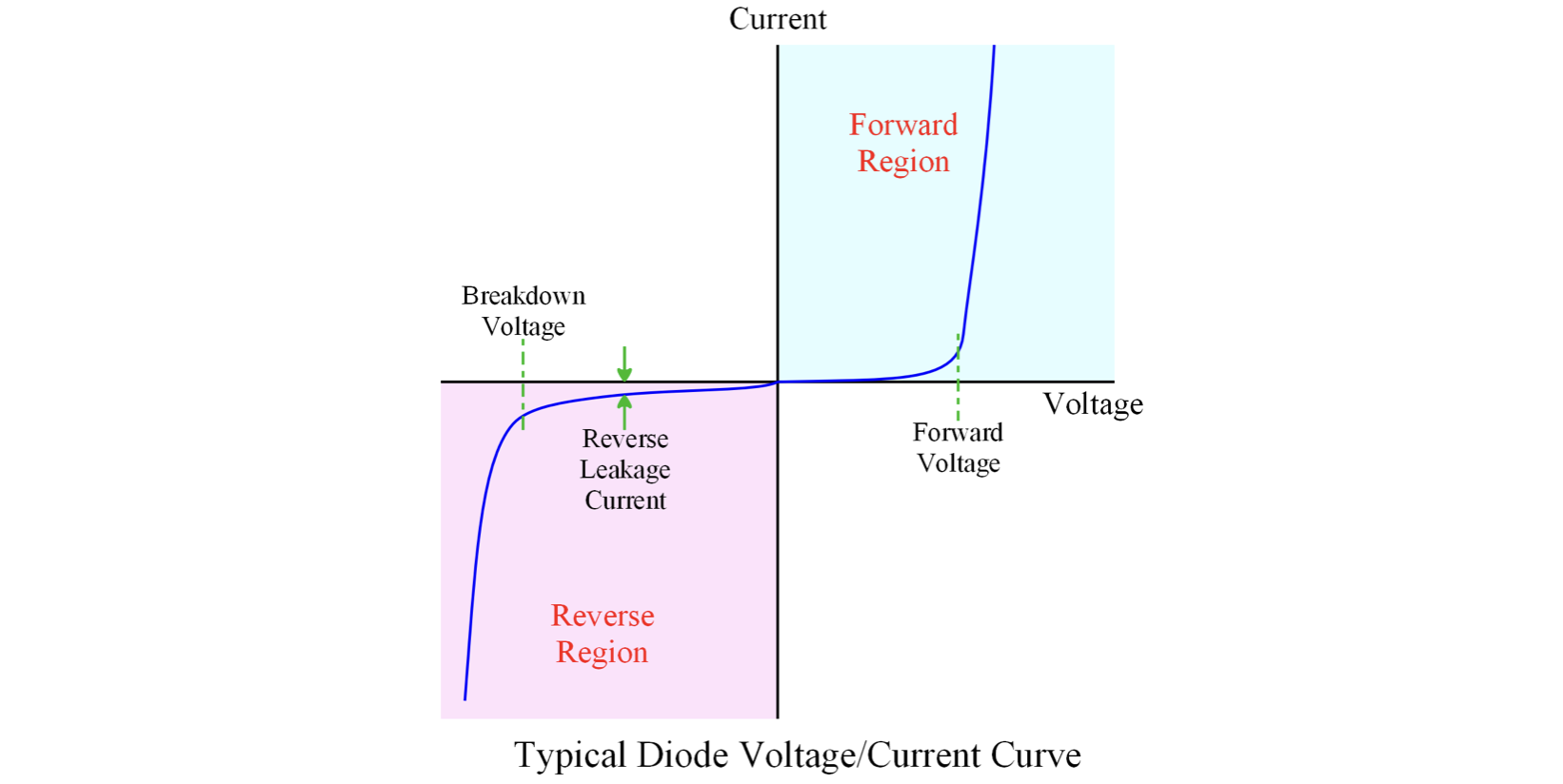
雪崩击穿
反向偏置电压达到某个临界值,半导体之间的电场足够强,使得少子拥有足够大动能,最终能够产生更多的载流子。更多的载流子意味着更多的少子,从而使上述过程不断循环,使得电流达到一个相当大的值。
齐纳击穿
反向偏置电压达到某个临界值,半导体之间的电场足够强,使得共价键被破坏,使得更多自由电子和空穴出现,在外加电场的作用下,大量载流子使得电流达到一个相当大的值。
二、二极管的直流分析
1. 模型
对于完全理想的二极管,在正偏时视为短路,在反偏时视为开路,称这种模型为理想模型(Ideal model)其特性曲线可以表示为
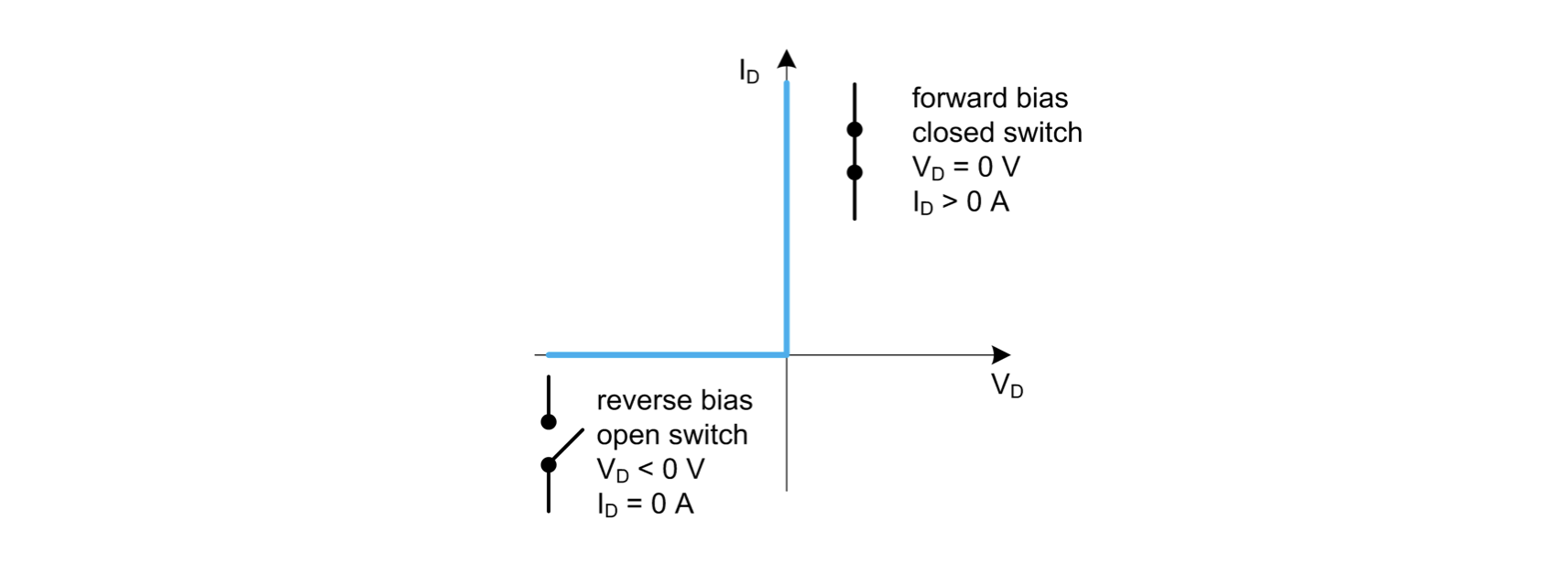
但实际上的二极管在正偏时存在一定的电阻和压降,因此更多地使用逐段模型(piecewise model)来替代理想模型,即将二极管内部看作是理想二极管、理想电压源和电阻的串联
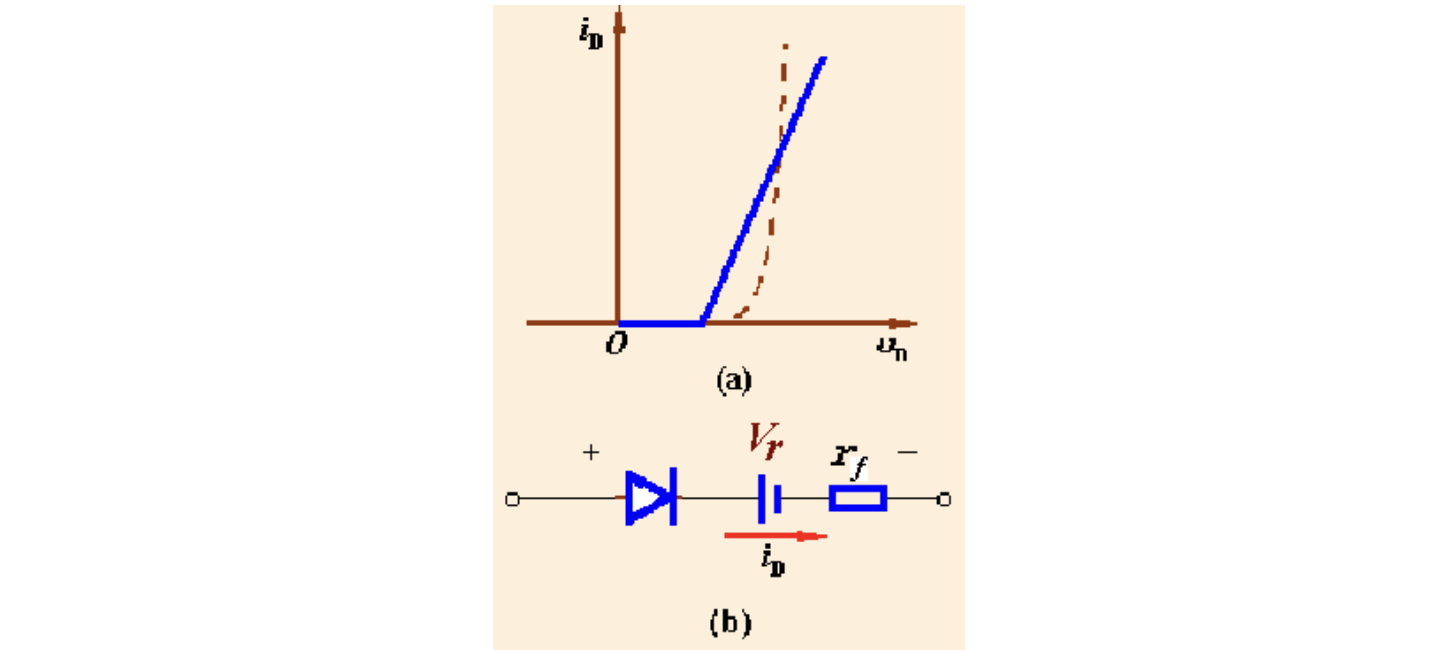
对于一般的硅二极管,一般认为
2. 直流分析
在直流分析时,通常采用图像法,先在图上作出二极管的特性曲线,再画出二极管两端的负载曲线,两条曲线的交点就是二极管实际的工作点,称此点为 「静态工作点」(quiescent point)或「Q 点」(Q-point)
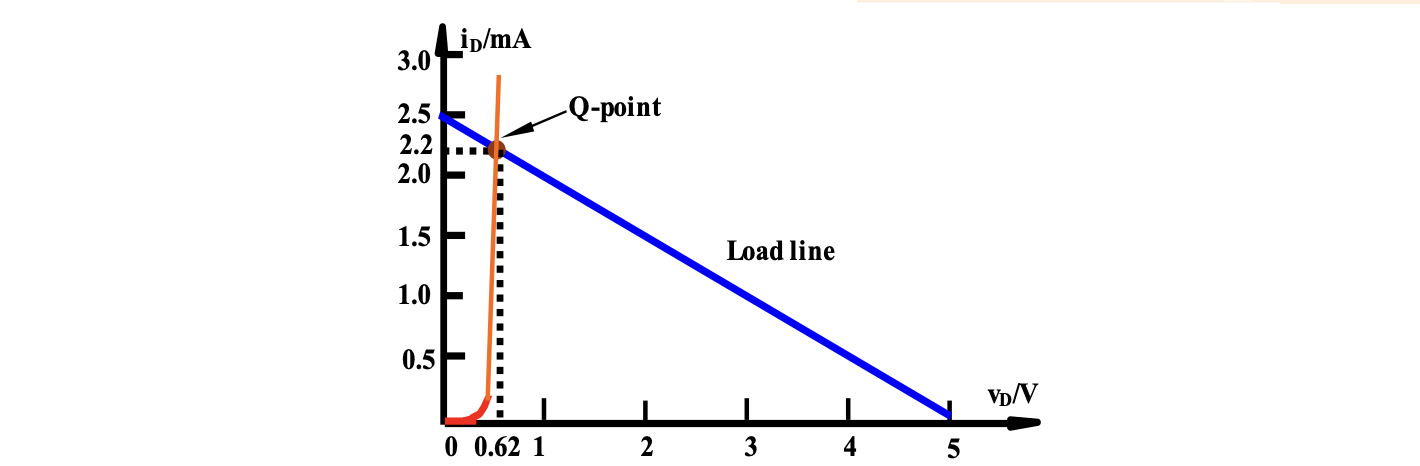
三、二极管的交流分析
1. 小信号模型
对于半导体的交流分析,若电压和电流的变化范围相对于直流部分较小,则通常采用一种被称为「小信号模型」(small signal model)的分析方法。对于任何一个交流电路,都可以将其分出直流分量和交流分量。半导体元件首先根据直流分量的大小,工作在指定的静态工作点,再在此静态工作点上叠加一个小交流信号,由此分析交流量的输出。例如对于流过半导体的电流
其中
2. 二极管的交流分析
等效电阻
前面已经提到,二极管正偏时的特性曲线可以表示为
如下图
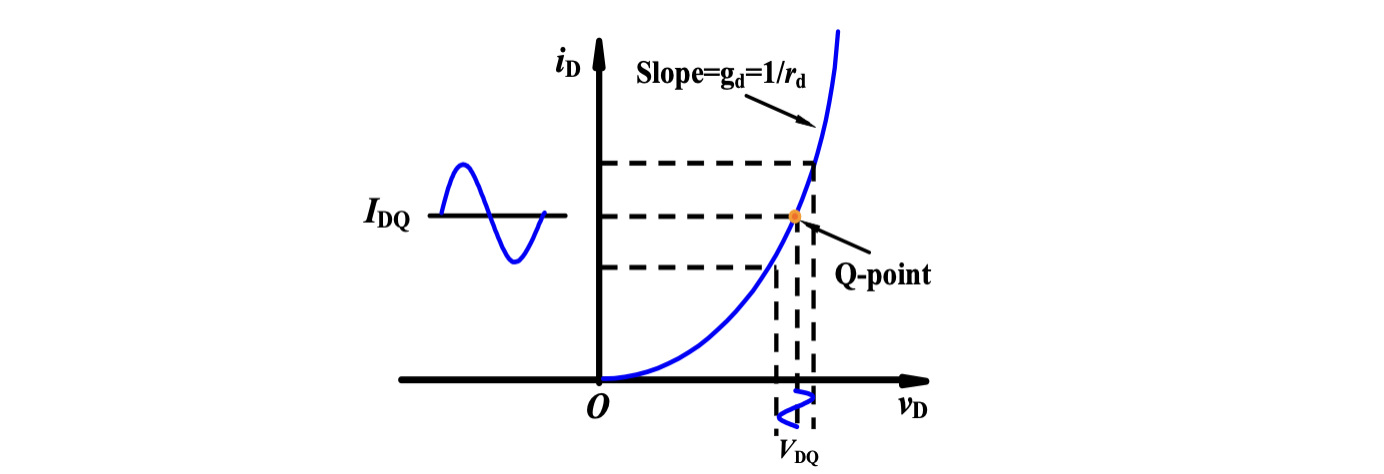
由于电压和电流的变化范围相对于直流部分较小,因此在半导体的电流-电压特性曲线上,通常将 Q 点附近的特性曲线视为直线。
根据小信号模型,交流信号通过二极管时,可以视为通过一个电阻,此电阻的电导值为静态工作点附近的曲线斜率
此时称直线的斜率的倒数为动态电阻(Dynamic resistance),与之对应的为静态电阻(Static resistance),即工作点到原点连线的斜率的导数。动态电阻的电导可以表示为
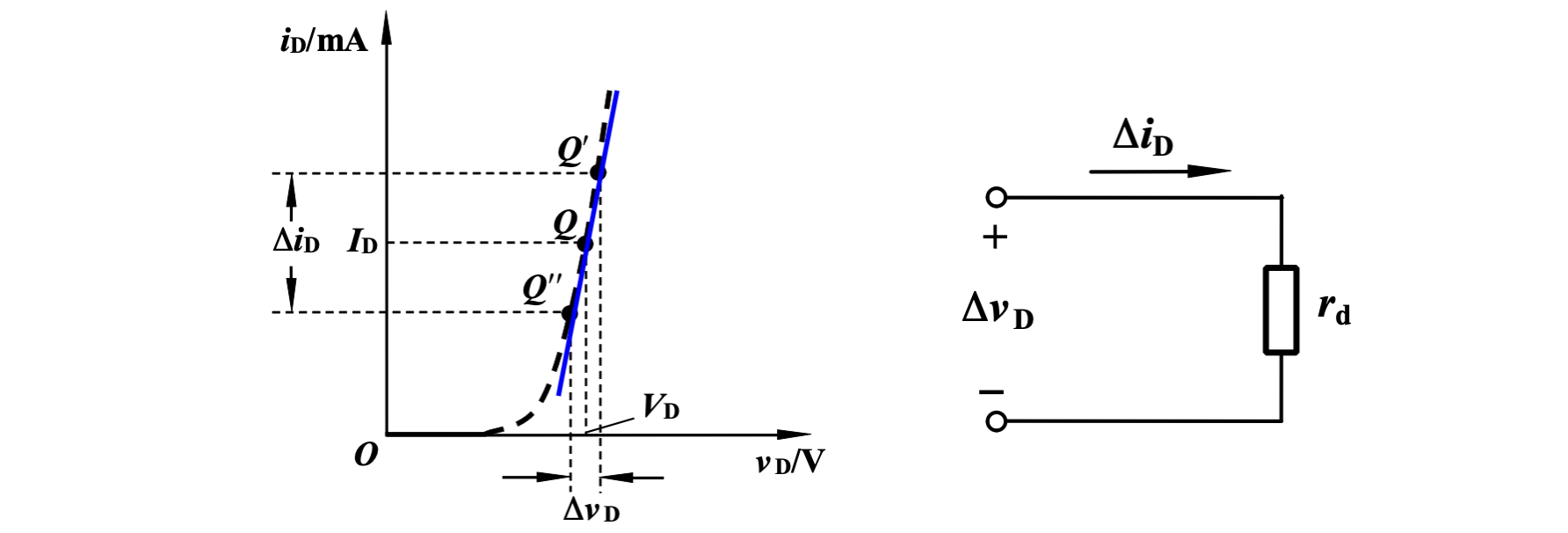
这样一来,半导体元件就可以视为一个简单的电阻
其中,
注意:为什么要使用电压对电流的导数来定义一个新的动态电阻呢?因为在交流工况下,我们要考察的是变化的电压产生变化的电流,因此只需要用伏安特性曲线的局部来表示交流工况下的电阻,因此对于二极管这种非线性元件,不能简单地使用传统方法计算出的静态电阻,而是必须考察在静态工作点附近的动态电阻,才能更好地衡量交流工况下的电阻。
2. 分析步骤
在实际的电路分析时,根据叠加原理,可以先将所有交流输入置零,让信号源为一个直流电源。在这种情况下,只需考虑直流状况,求出二极管的静态工作点。
此时一般不考虑二极管的直流电阻,而是直接计算压降,如
接下来再将二极管替换为一个交流电阻,计算公式参照上文,用热电压和静态电流去计算。
四、常见的二极管
1. 太阳能电池
太阳能电池(Solar Cell)能从太阳能板阵列中获得能量来给电子产品供电
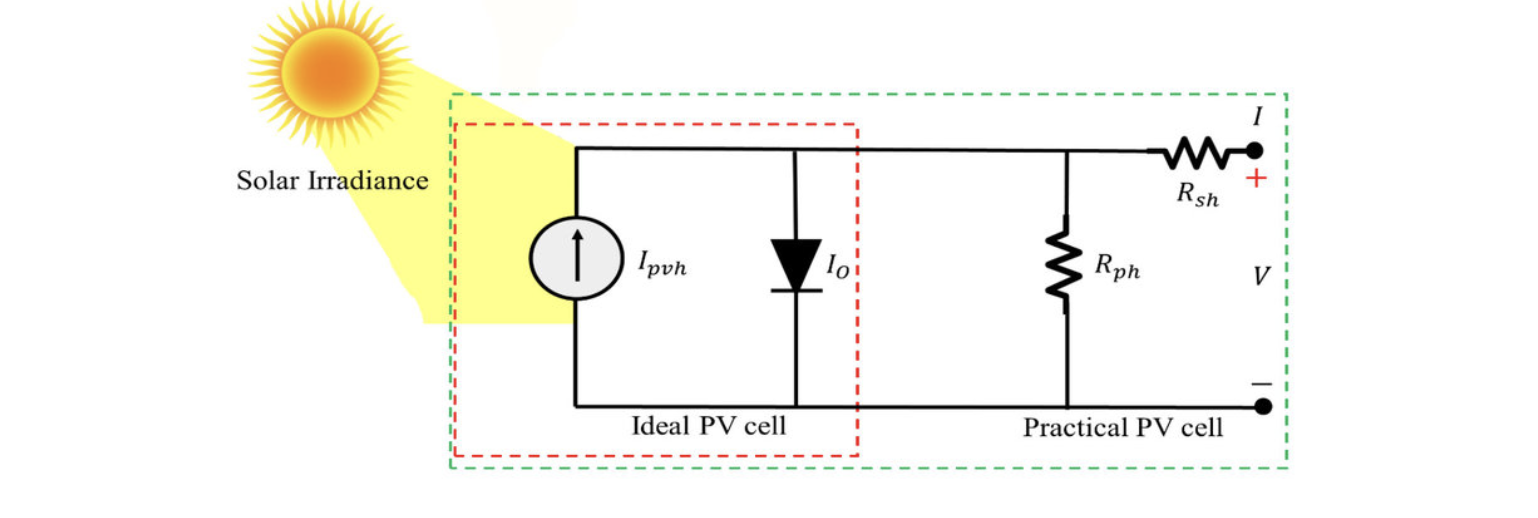
理想的太阳能电池由一个恒流源和一个二极管构成。
2. 光电二极管
光电二极管(Photodiode)和普通二极管一样,也是一个由 PN 结构成的半导体器件,也具有单向导电性,但其主要用于将光信号转换为电信号。
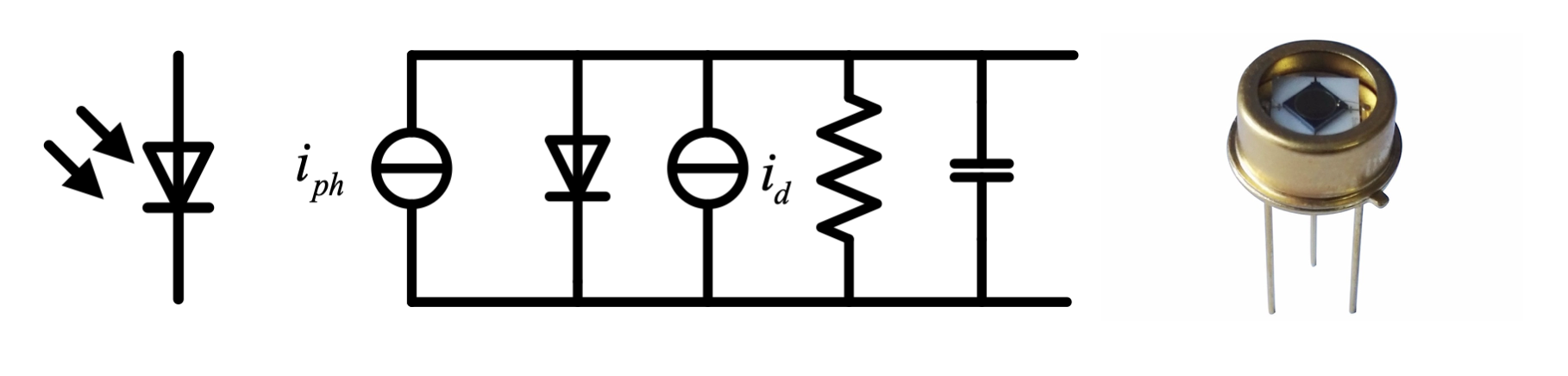
3. 发光二极管
发光二极管(Light-Emitting Diode),即 LED,可以将电能转换成光能

4. Schottky 势垒二极管
肖特基势垒二极管(Schottky Barrier Diode)是一种高频二极管,在二极管内部没有留存的少子,因此它在正偏和反偏两种状态之间切换的速度远大于 PN 结构成的普通二极管。
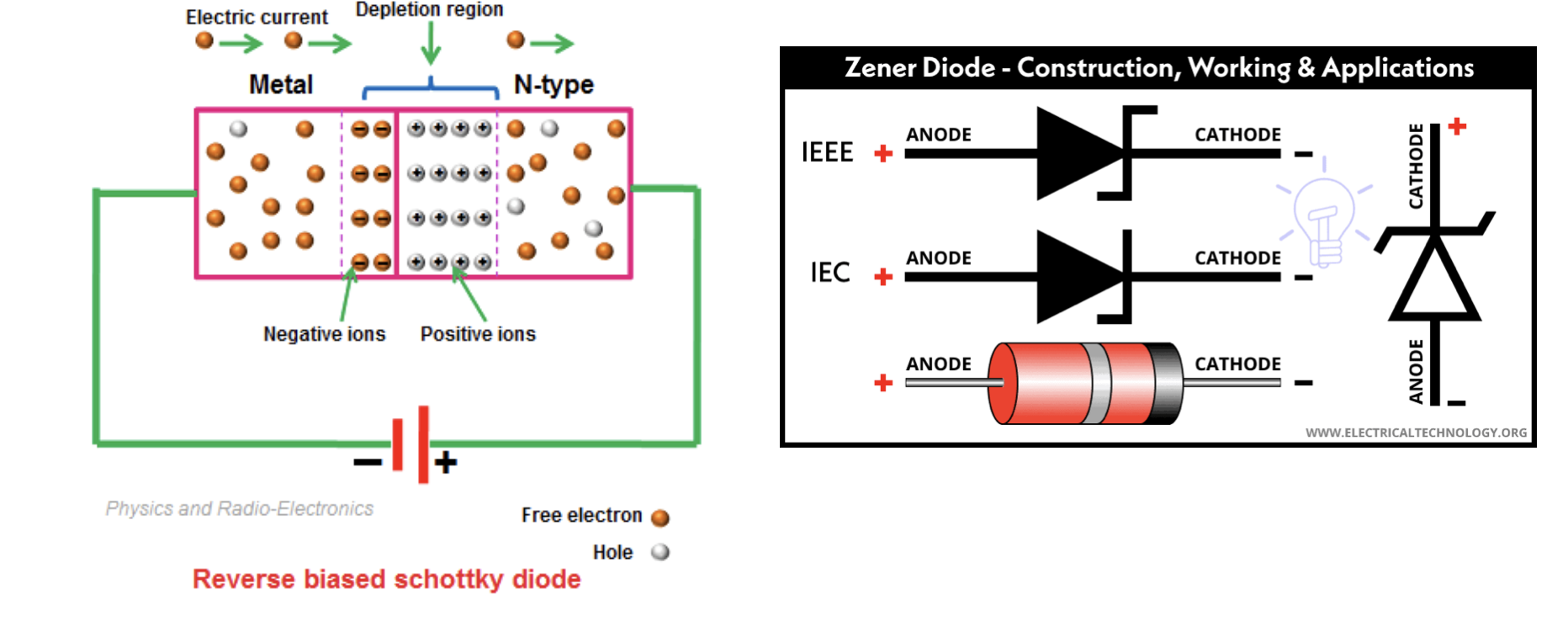
5. Zener 二极管
Zener 二极管利用齐纳击穿在反向击穿区可以实现电流很大而电压基本不变的特性,因此又被称为「稳压二极管」,这一特性在之后涉及的稳压器中大量使用
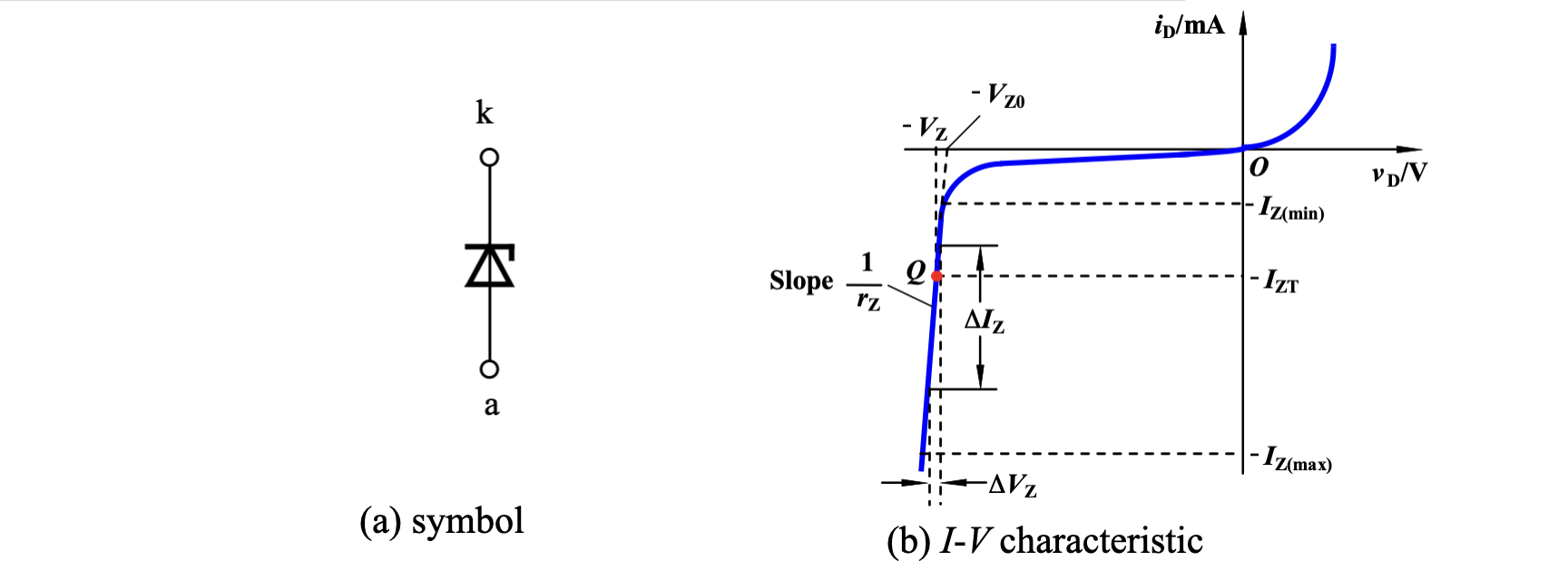
Zener 二极管的主要参数有
- Zener 击穿电压
- 增量电阻
- 反向最大电流
三、二极管的应用电路
1. 整流器
多数电子产品都需要直流供电,而市电提供的是交流电。为了得到可用的直流电,需要:
- 首先通过降压器得到电压较低的交流电
- 然后通过二极管整流得到正半波。
- 通过 RC 电路进行滤波
- 最后通过稳压器实现稳定的直流输出。
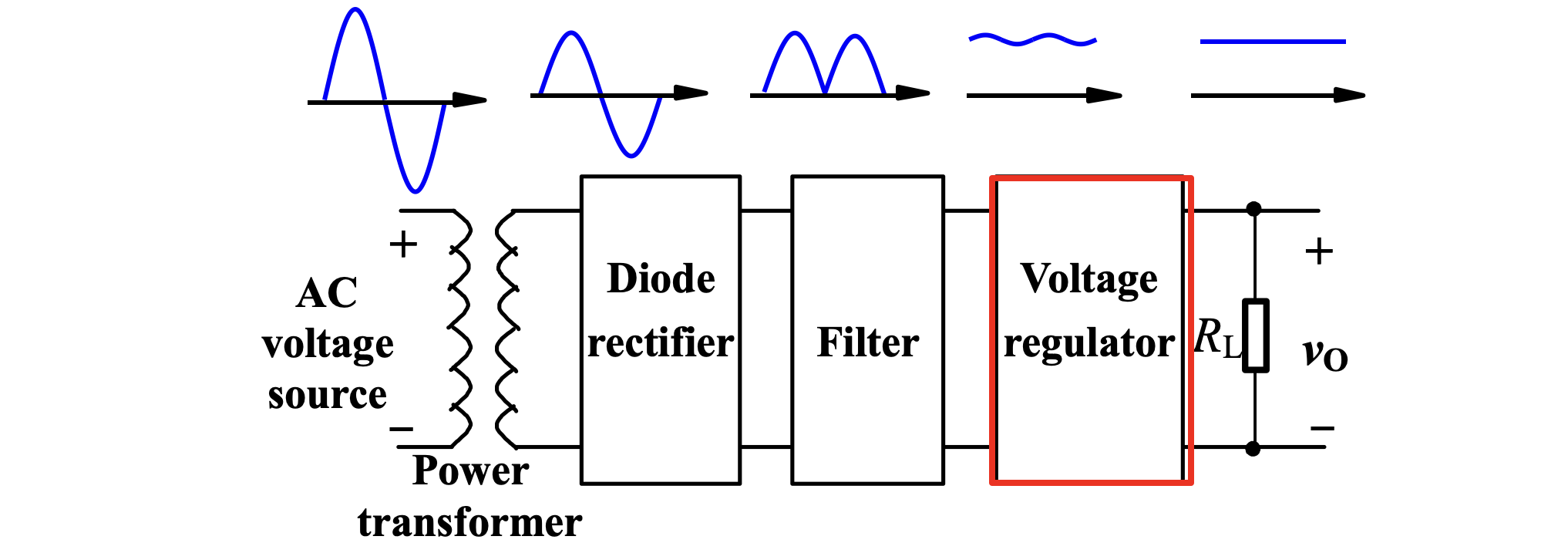
将正负变换的交流电压转变为单向脉动电压的过程称为「整流」(Rectification),根据单向脉动电压的波形可以分为「半波整流」(Half-wave rectification)和「全波整流」(Full-wave rectification)
半波整流器
通过一个简单的二极管,就可以实现最基本的半波整流器。如图
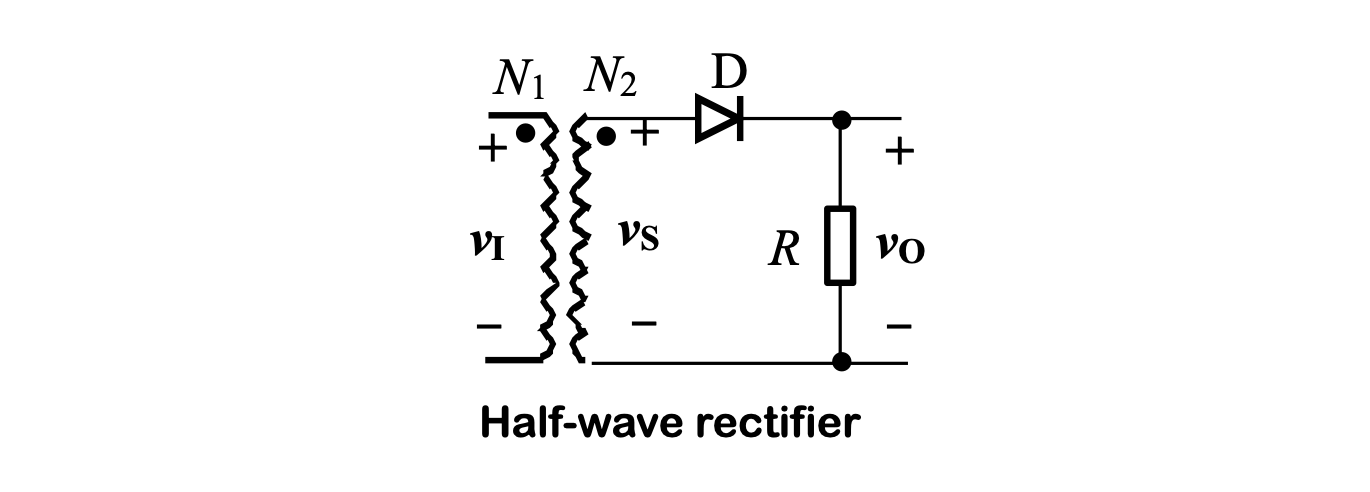
根据二极管的单向导通性:
,
得到输出波形为:
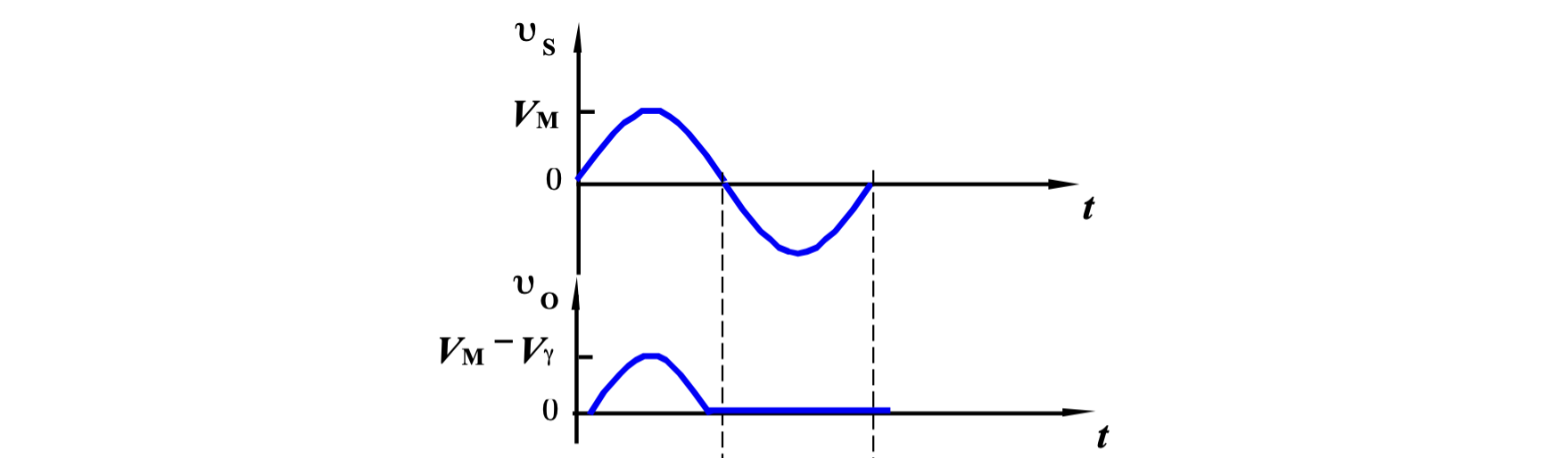
全波整流器
实现全波整流的方法也非常简单,只需要分别用两个二极管将输入电压传递给负载即可。由此原理可以得到中心抽头式(Center-tapped)全波整流器

根据二极管的单向导通性:
时 , 均 截 止 ,
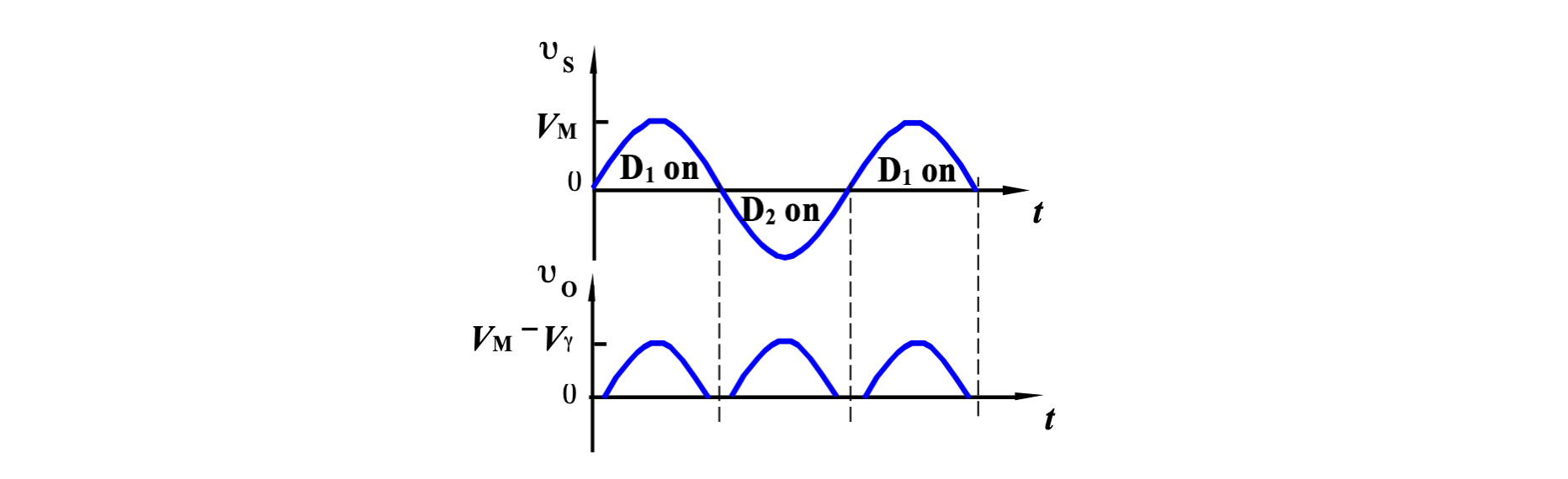
桥式整流器
对于上文介绍的全波整流器,截止的二极管需要承受
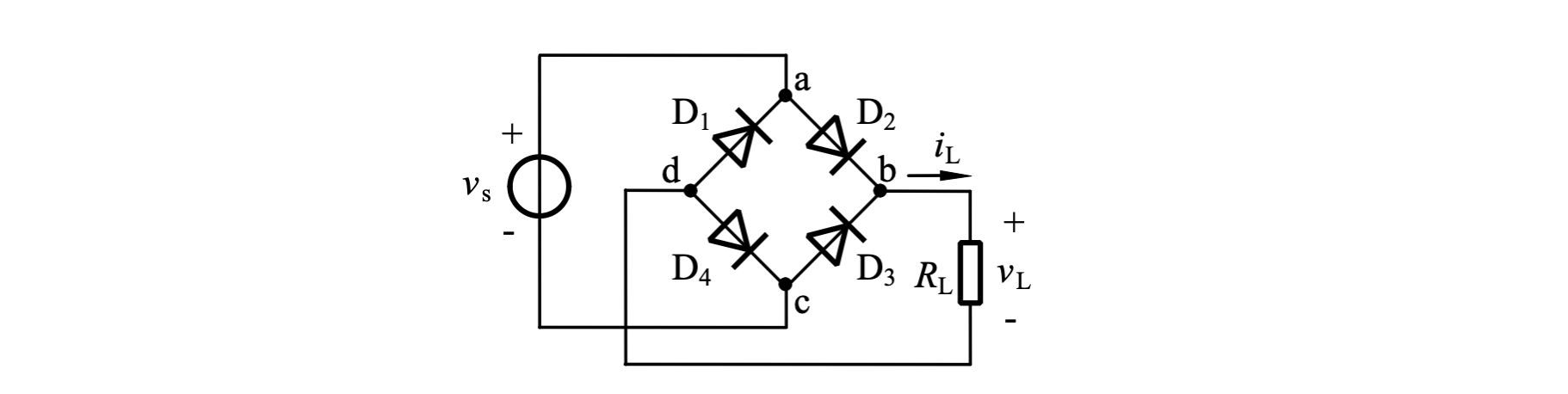
相比中心抽头式全波整流器,桥式整流器的最大反向电压为
2. 限幅器
为了电子元件的安全工作,有时候需要对信号的波幅做限制,此时可以使用二极管构成「限幅器」(Clipper)
将二极管和一个电压源串联,即构成单二极管限幅器
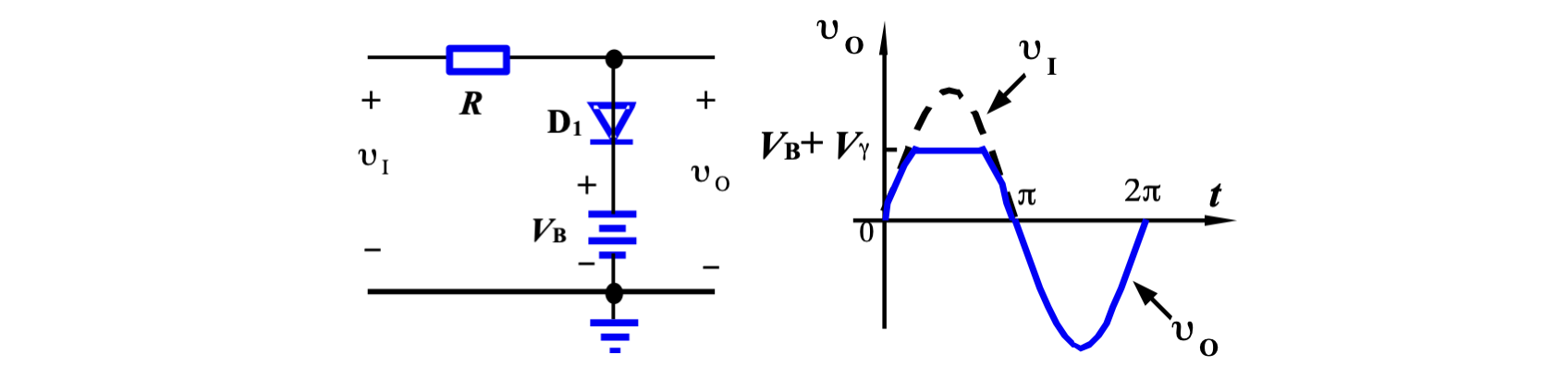
但此电路只能对正半波做限幅,因此可以再加一路单二极管限幅器,构成双限幅器(Double limiter)
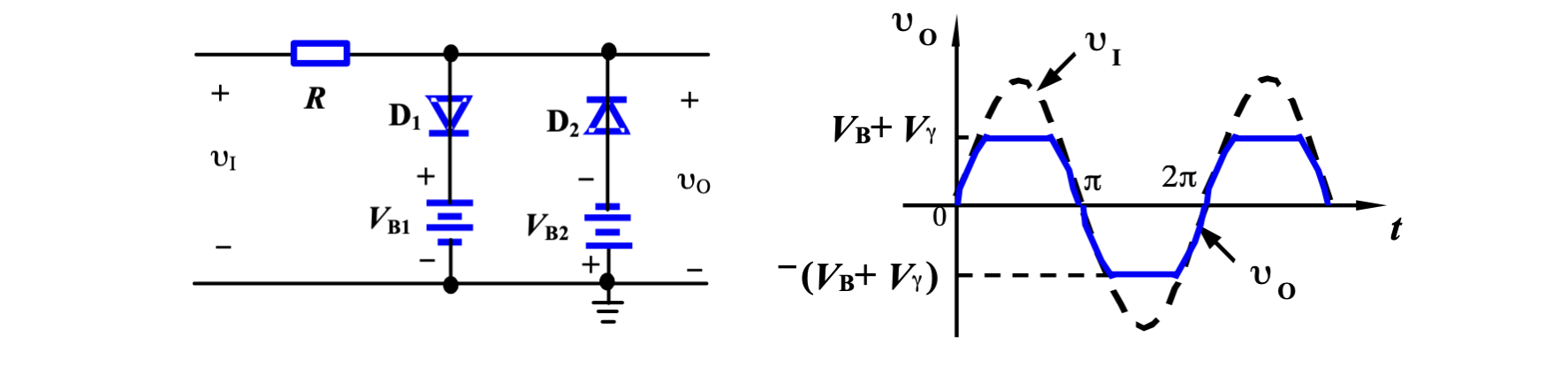
3. 钳位器
为了让周期性变化的波形的顶部或底部固定在某一直流电平上,可以用电容和二极管组成钳位器(Clamper),如下图
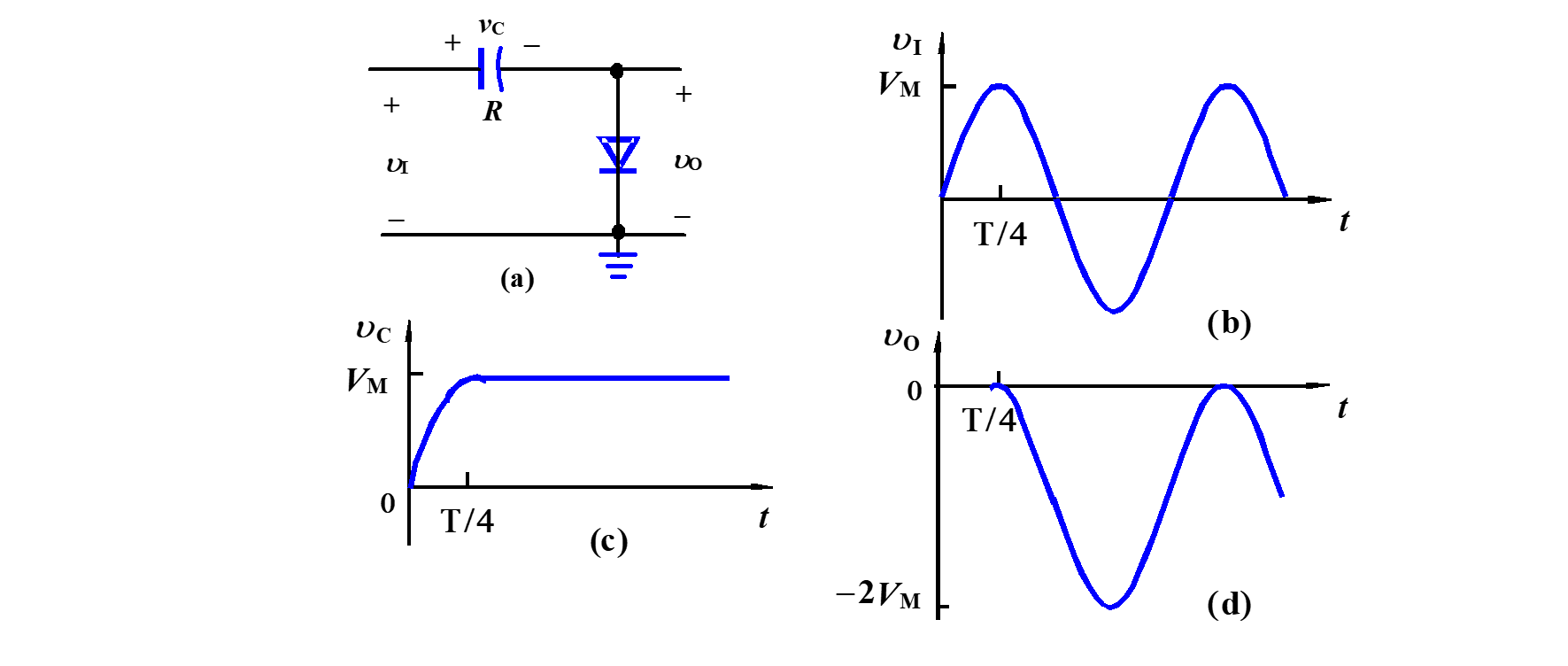
在二极管单向导电的限制下,电容只能被充电而不能放电,当电容充满电,
4. 多二极管分析
分析在含有一个或多个二极管的电路时,先假定所有二极管均截止,根据其他已知条件算出其两端电压后,在判断是否导通,若仍不导通,则结果正确,若导通,则需以导通为实际情况代入重新计算
考试要求
必考桥式整流器,因为电源那道大题必考。