IC 设计
除了 MOS 和反馈之外第三个比较重要的点
本章解释运放的一些具体应用,解释比较器电路。需要分析有源滤波,如何设计和产生振荡,以及如何制作稳压器。
都可能作为考试题目来考
一、滤波器
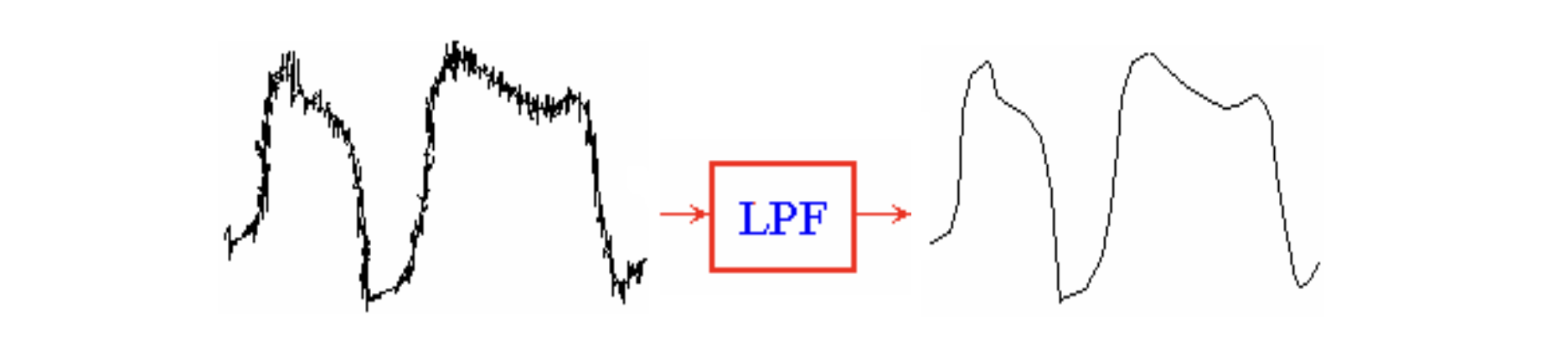
在实际电路中,经常会出现低频信号上叠加了很多高频毛刺,从而出现不稳定波形,如何把波形变得平整一点?此时就可以通过一个「低通滤波器」(Low Pass Filter)LPF,去除高频毛刺。
1. 常见无源滤波器
通过简单的 RC 电路可以实现滤波器的作用。这些滤波器不需要外加电源供电,因此被称为「无源滤波器」
判断滤波器类型的方法很简单,一种是直接求其传递函数
1.1 高通滤波器
如图所示 RC 电路,电容和电阻串联,输出端接在电阻处。
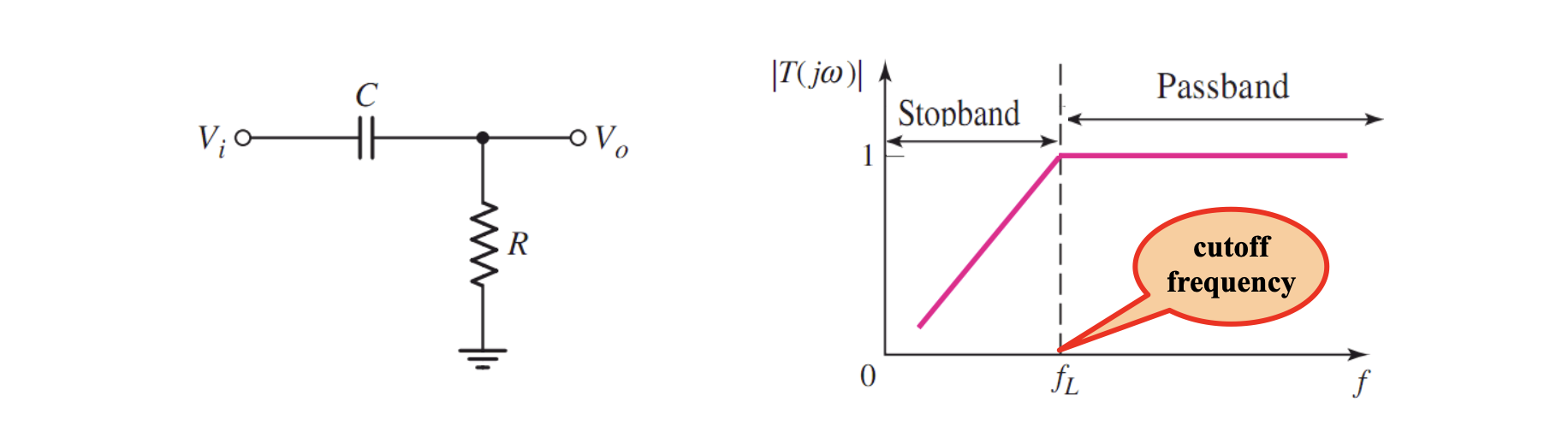
用传输函数来表示
令
当
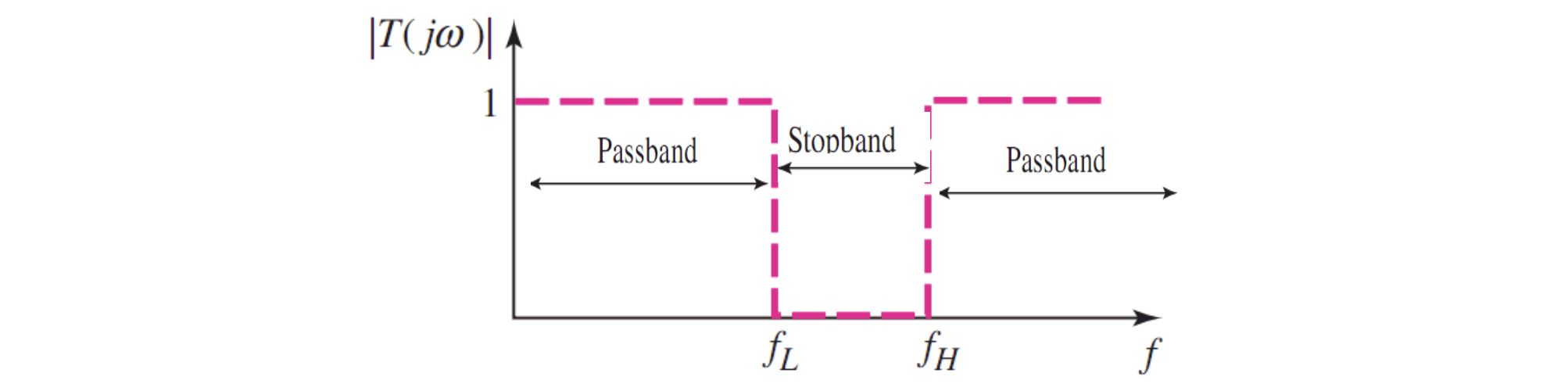
在频域上可以做出其幅频特性曲线,在理想情况下,幅频特性区间仅有两条直线构成,如上图。信号被筛选掉的频率部分称为阻带 (Stopband),能通过的部分叫做通带 (Passband),之间的分界频率称为截止频率(Cutoff frequency)
1.2 低通滤波器
如图所示 RC 电路,电容和电阻串联,输出端接在电阻处。
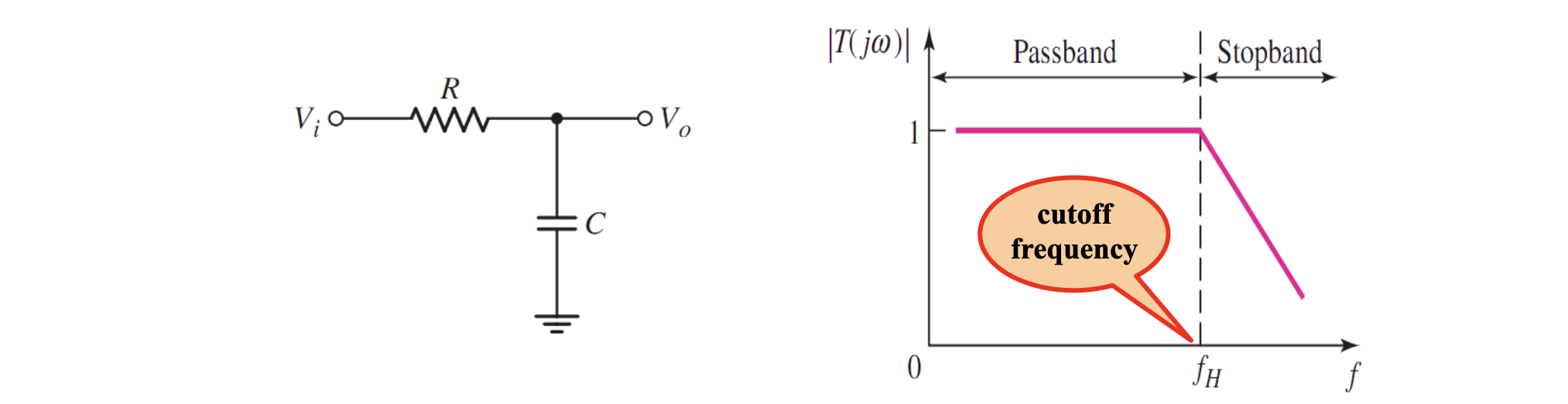
用传输函数来表示
令
当
1.3 带通滤波器
通过低通滤波器和高通滤波器的组合,还可以实现只有某一部分频率通过的滤波器,称为「带通滤波器」(Bandpass filter)
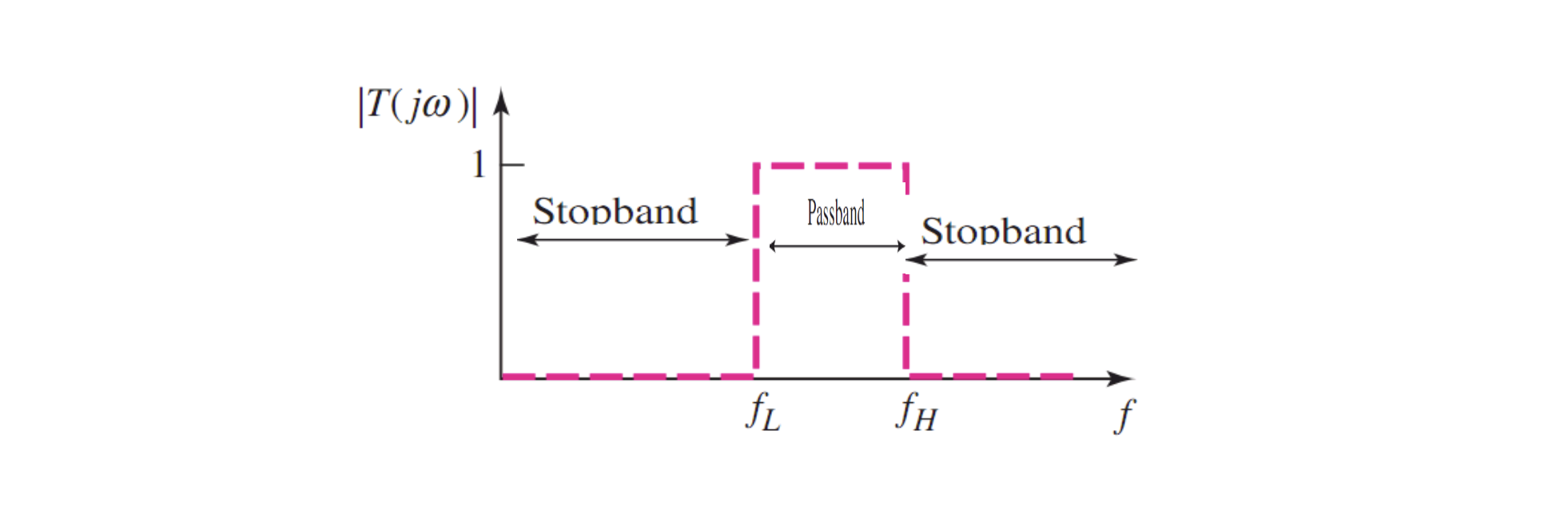
1.4 带阻滤波器
以及只有某一部分频率无法通过的滤波器,称为「带阻滤波器」(Band-reject filter)
1.5 全通滤波器(All-pass filter)
频率全通,但是存在相移
2. 有源滤波器
2.1 有源滤波器的引入
无源滤波存在很多的缺点
- 带负载能力差,在
- 放大倍数无法超过
- 幅频响应特性曲线上升/下降沿不够陡峭,引进了带外信号
如何消除缺点?逐一分析。带负载能力可以通过在输出端接上电压跟随器来解决,而放大的功能,只需要对电压跟随器进行修改,改成同相放大器,如下图
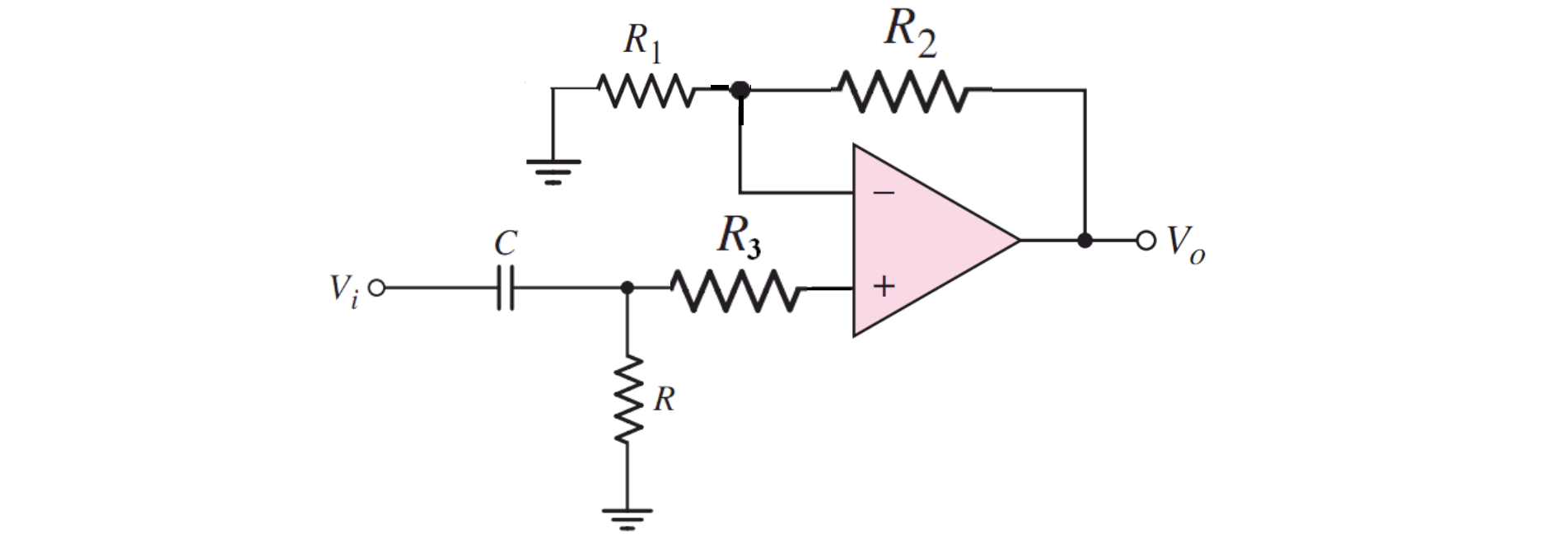
为了使上升/下降沿更加陡峭,可以再加一阶 RC 电路,但就可能导致
2.2 传输参数的推导
如图为双极点滤波器
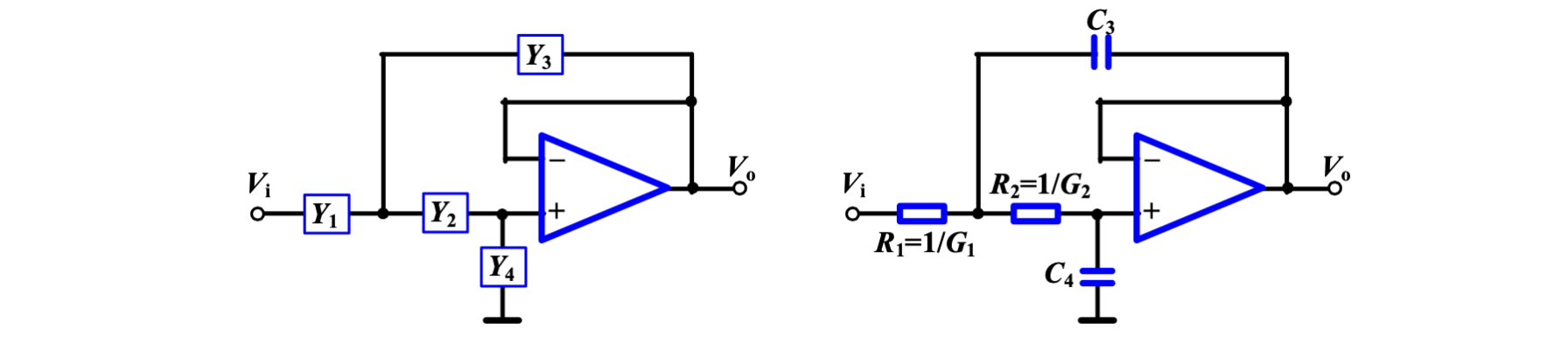
如果用导纳参数,求
用电导表示,则为
当
当
因此此电路为低通滤波器
会引入正反馈,电路包括正反馈和负反馈,电容那条是正反馈
2.3 Butterworth 滤波器
低通 Butterworth 滤波器
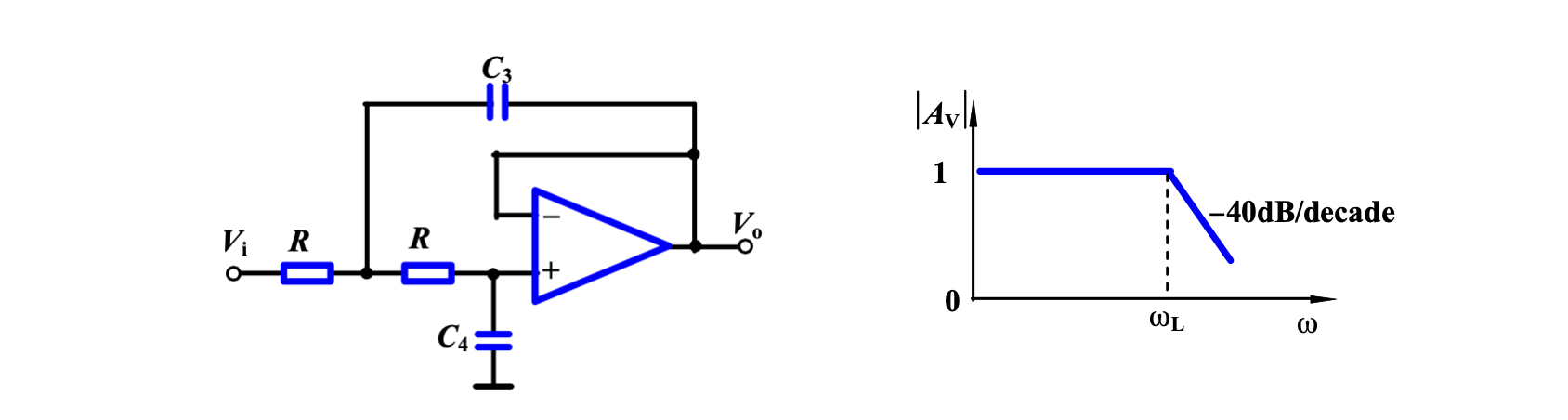
传输函数为
令
平方再开根号得到其幅值
为了要更快衰减,得到最大平坦滤波器,幅频响应对
因此原式化为
得到截止频率
高通 Butterworth 滤波器
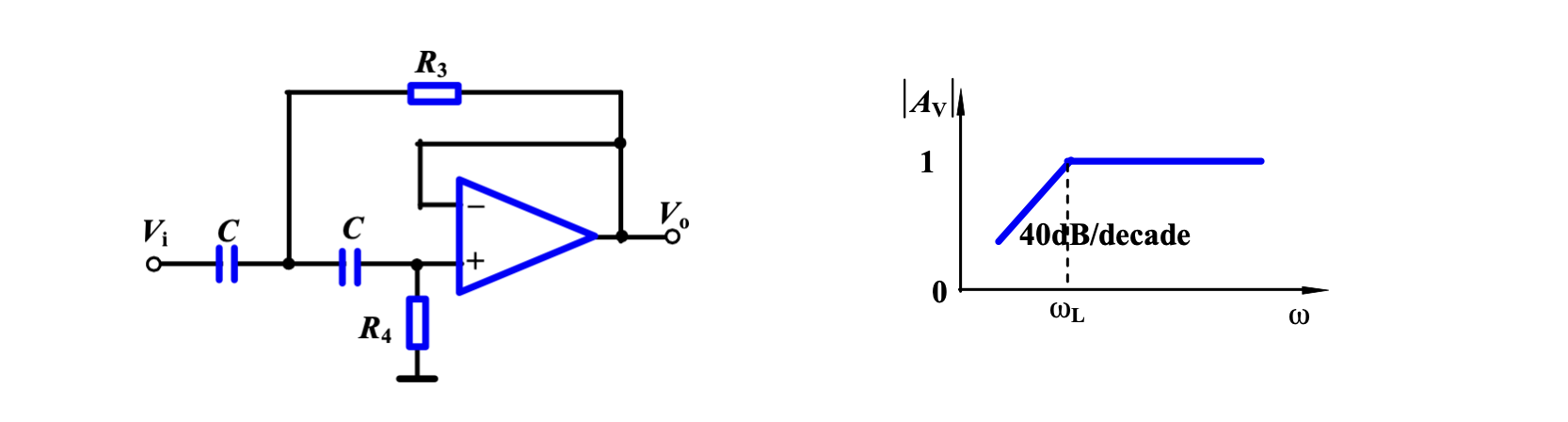
交换低通滤波器中的电容和电阻,可以得到高通滤波器
得到截止频率
通过合理设计,可以实现低通滤波器串高通滤波器,实现带通滤波器
高阶滤波器
N 阶 Butterworth 低通滤波器
N 阶 Butterworth 高通滤波器
二、振荡器
1. 振荡的基本概念
负反馈产生的移相可能产生振荡,振荡的瞬间,电路从负反馈变成正反馈。振荡平衡时需要满足
振荡器在通电的瞬间就能产生振荡信号,但这个信号从何而来呢?来源于电路中广泛存在的电子噪声,其频谱分布非常广泛。
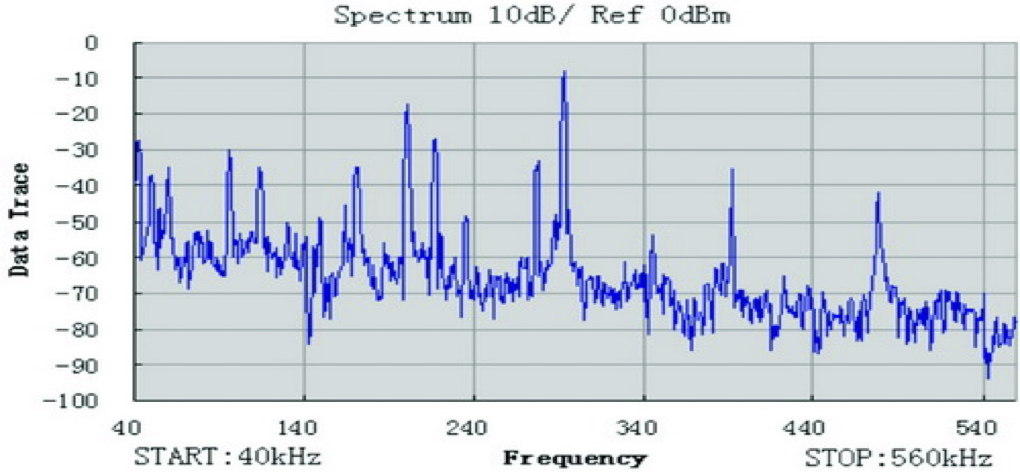
因此振荡器的工作原理就是从噪声中通过滤波器选取需要的频率,不断的放大。在起始阶段满足
但如果一直让
因此不仅需要正反馈网络,还需要滤波器,并且在某一时刻,需要用负反馈抑制正反馈的无限进行,使得
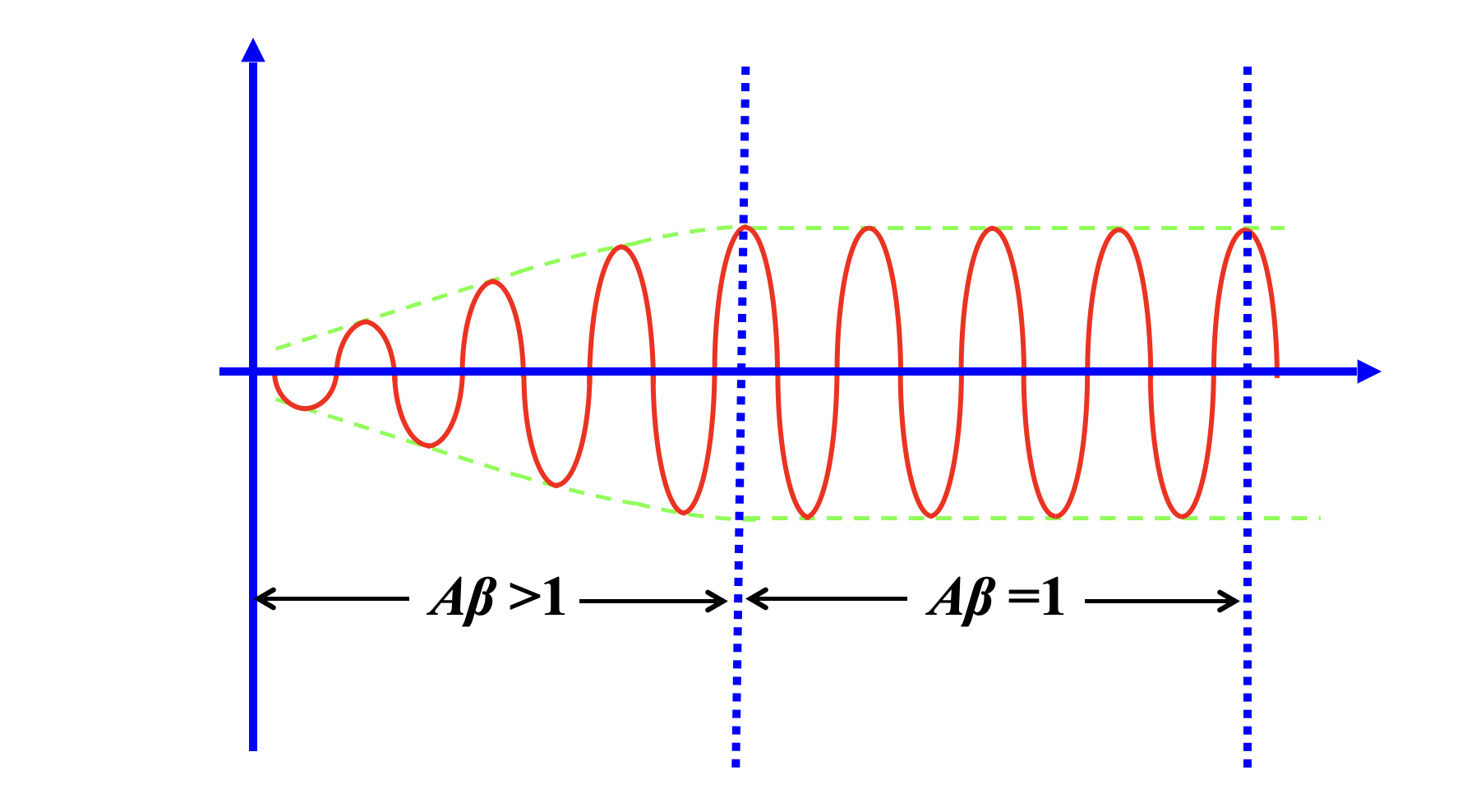
因此振荡分为两个阶段
- 前半部分
- 后半部分
2. 振荡器的移相
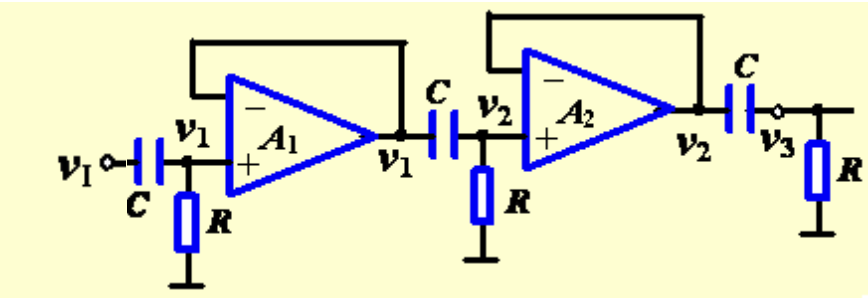
如图,三级 RC 电路构成了一个振荡器,其中
对于单级传输函数有
把后级输入电阻看作前级的负载,因此总传输函数为三级传输函数之积
在三级 RC 电路之后加上一个放大器,并引入反馈
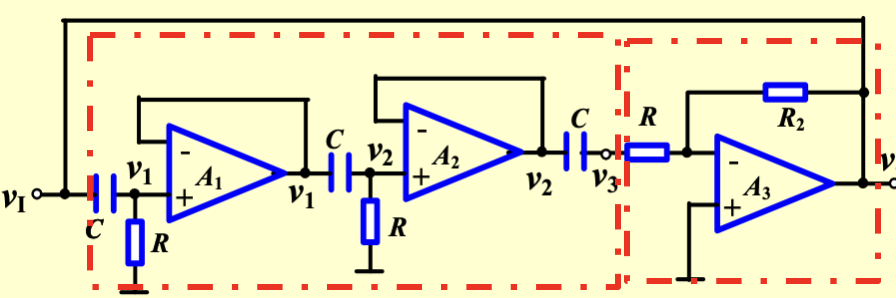
此电路的左侧红框为反馈网络,将反馈信号引到放大器的反相输入端,同时进行了「频率选择」,右半部分为放大器。由三级 RC 电路的结论有
对于放大器而言,是一个简单的反相比例放大器,满足
由此得到传输函数
令
为了实现振荡,需要令传递函数虚部为零,即
由此体现了上文提到的频率选择特性,即只有满足此条件的频率才能实现振荡。得到此振荡器的振荡频率(Oscillation frequency)
当
得到 T 的模条件
因此振荡平衡时需要满足
图中的两个电压跟随器其实是不必要的,如果要去掉,如下图
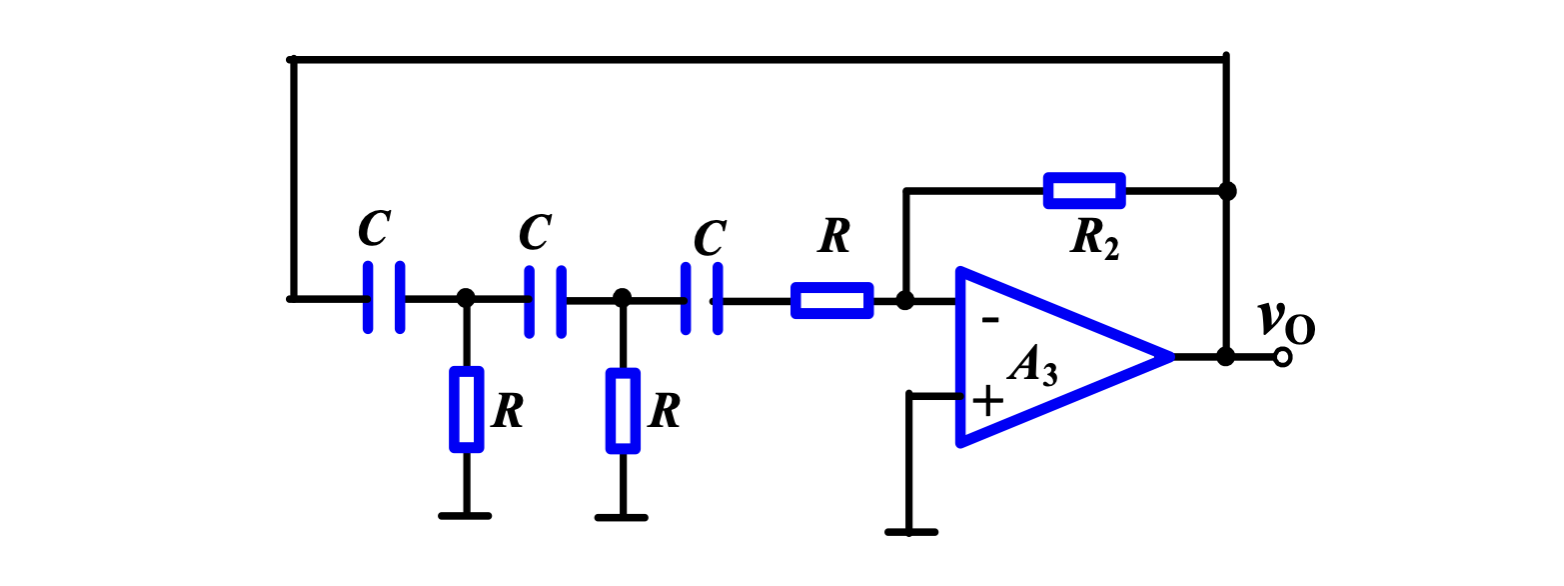
则此时的振荡频率为
放大器的电阻比率为
即为了实现起振,需满足
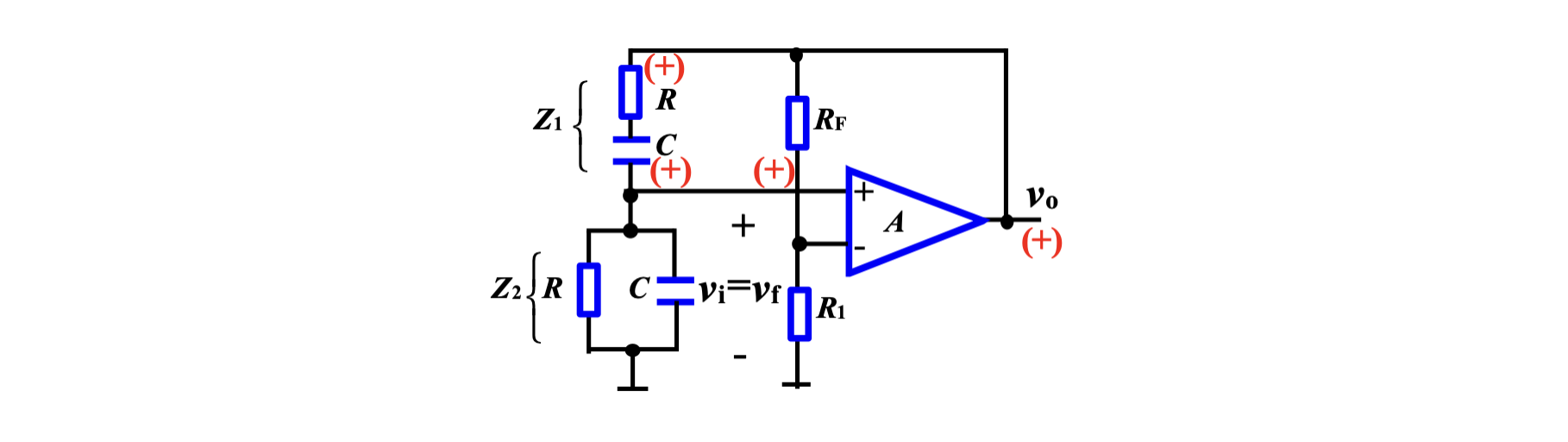
3. Wien 电桥振荡器
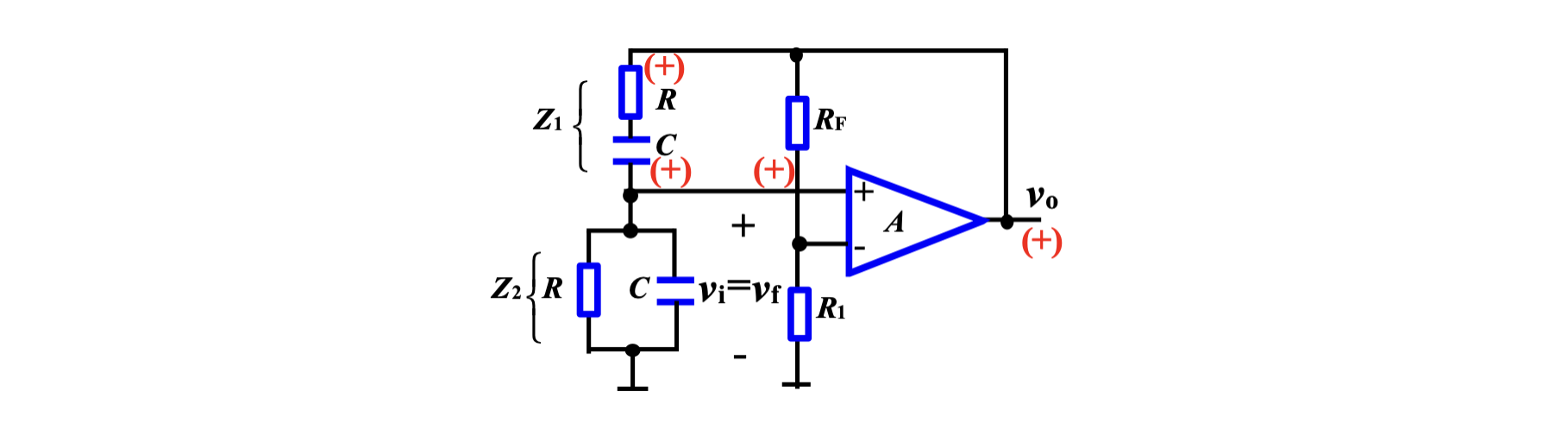
左侧电路为 RC 串联和 RC 并联网络,完成了频率选择,也送到了同相输入端引入正反馈;而反相输入端的两个电阻构成同相比例放大器。按照反馈理论中的结构图, 右侧的运放,
对于右侧同相比例放大器而言,有
对于反馈网络而言
令
根据
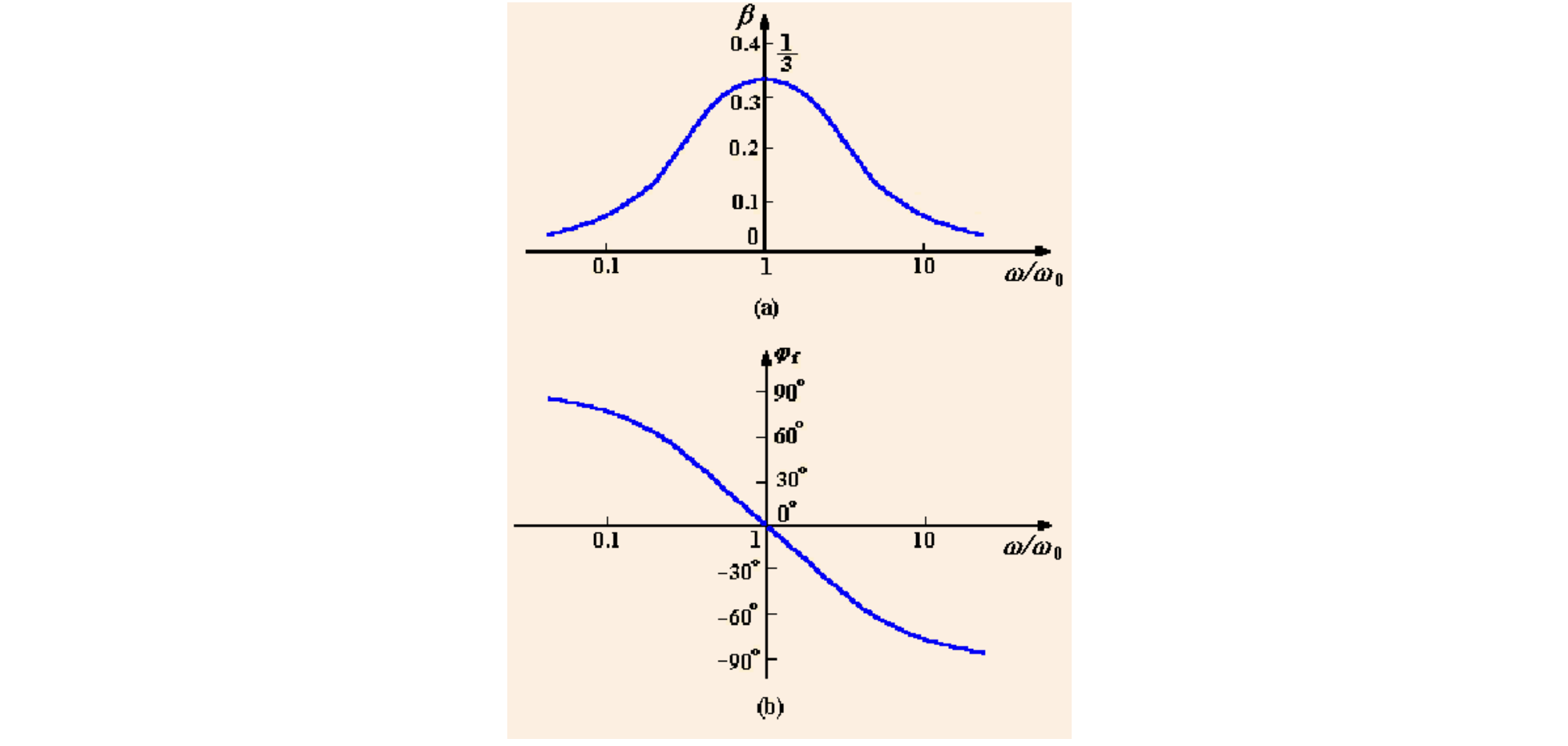
发现
若选择
由于送到同相输入端,显然相移为
热敏电阻法
将
二极管法
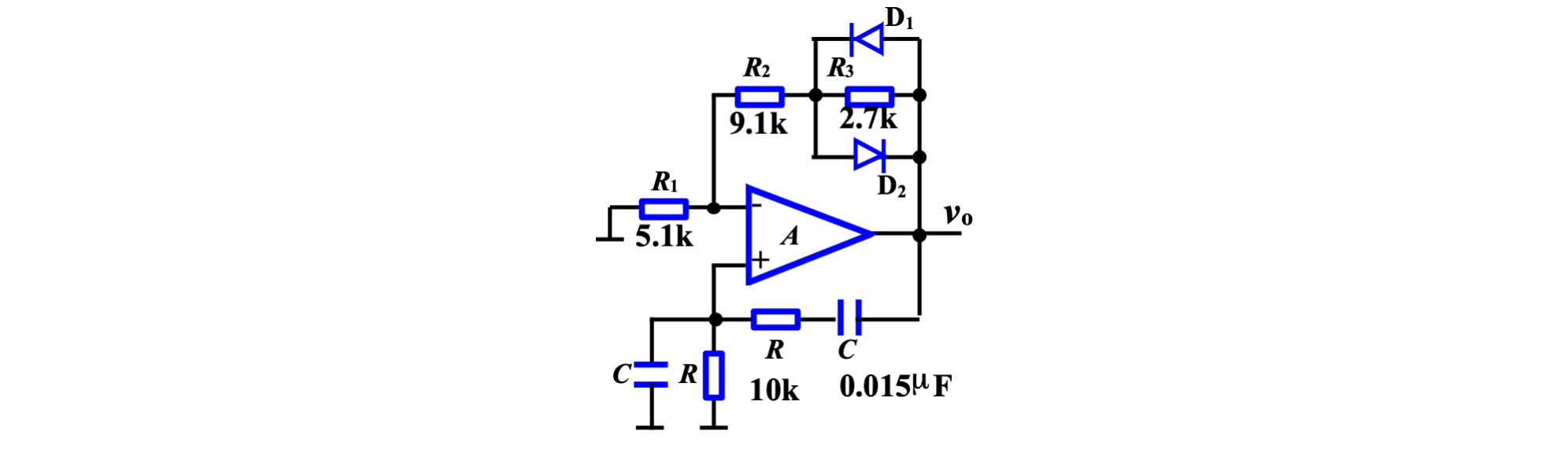
根据二极管分析法,在开始分析时认为二极管均不导通。事实上也确实如此。在起振阶段,
其中
由于
三、Schmitt 触发器
振荡器可以产生正弦波,但有时候需要非正弦波
1. 比较器
比较器(Comparator)能够比较输入端的两个电压信号的相对大小,并在输出端产生相应的输出。在比较器中没有负反馈,因此虚短特性不成立。
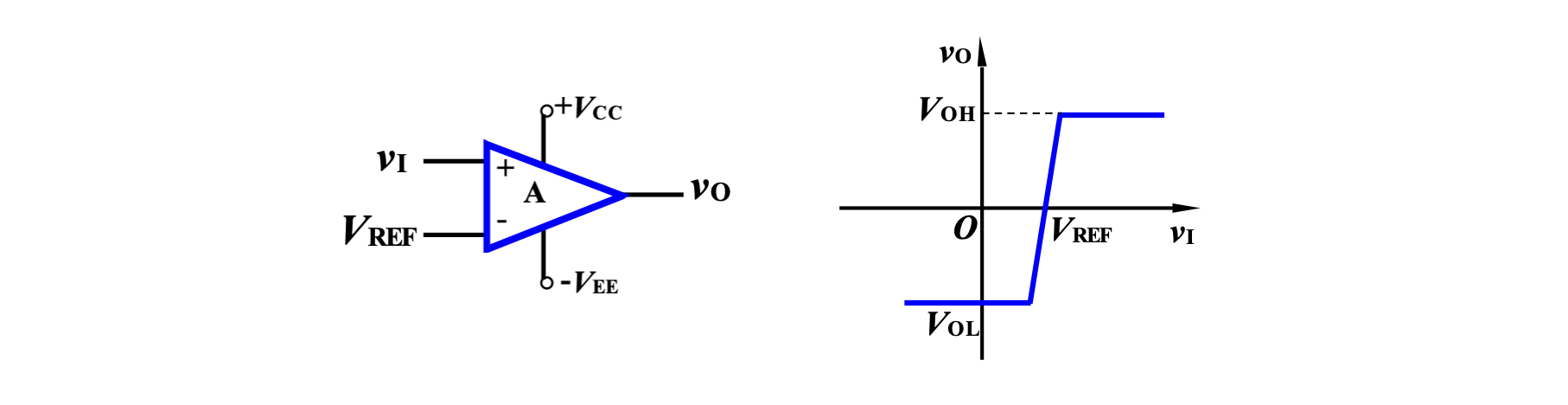
输入端之一为输入电压
1.1 输出特性
若不考虑输出极饱和压降,则将
特例:当
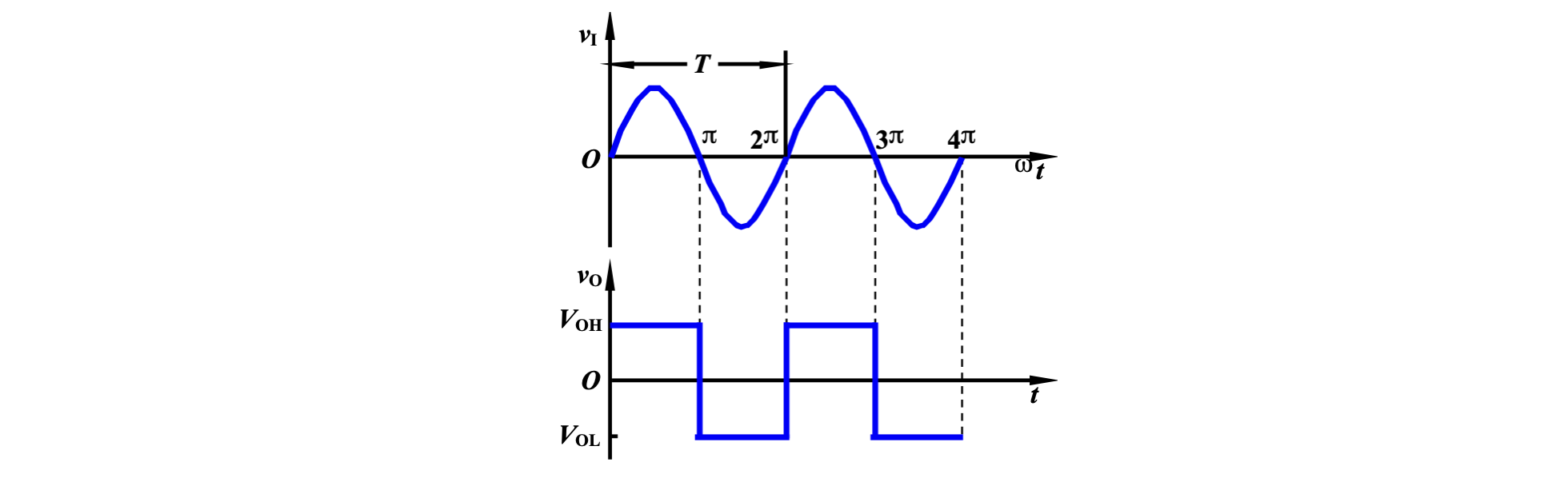
若
利用叠加原理,还可以实现对参考电压进行「运算」得到交越电压,如图
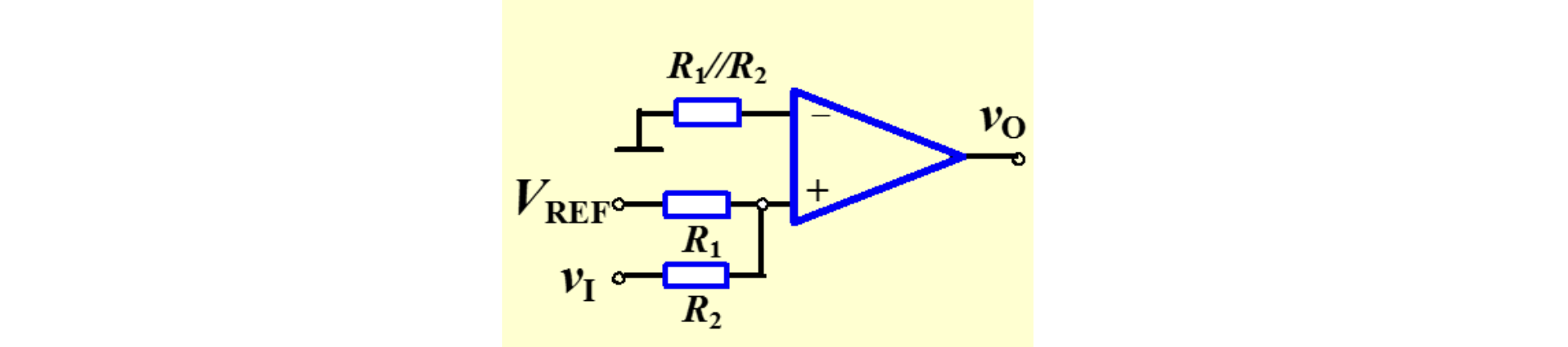
根据叠加原理有
此时的交越电压为
1.2 比较器的衍生
脉冲发生器
在比较器后面加入一个 RC 电路构成的微分器,再加入一个二极管作半波整流,可以将方波转换为单向脉冲。
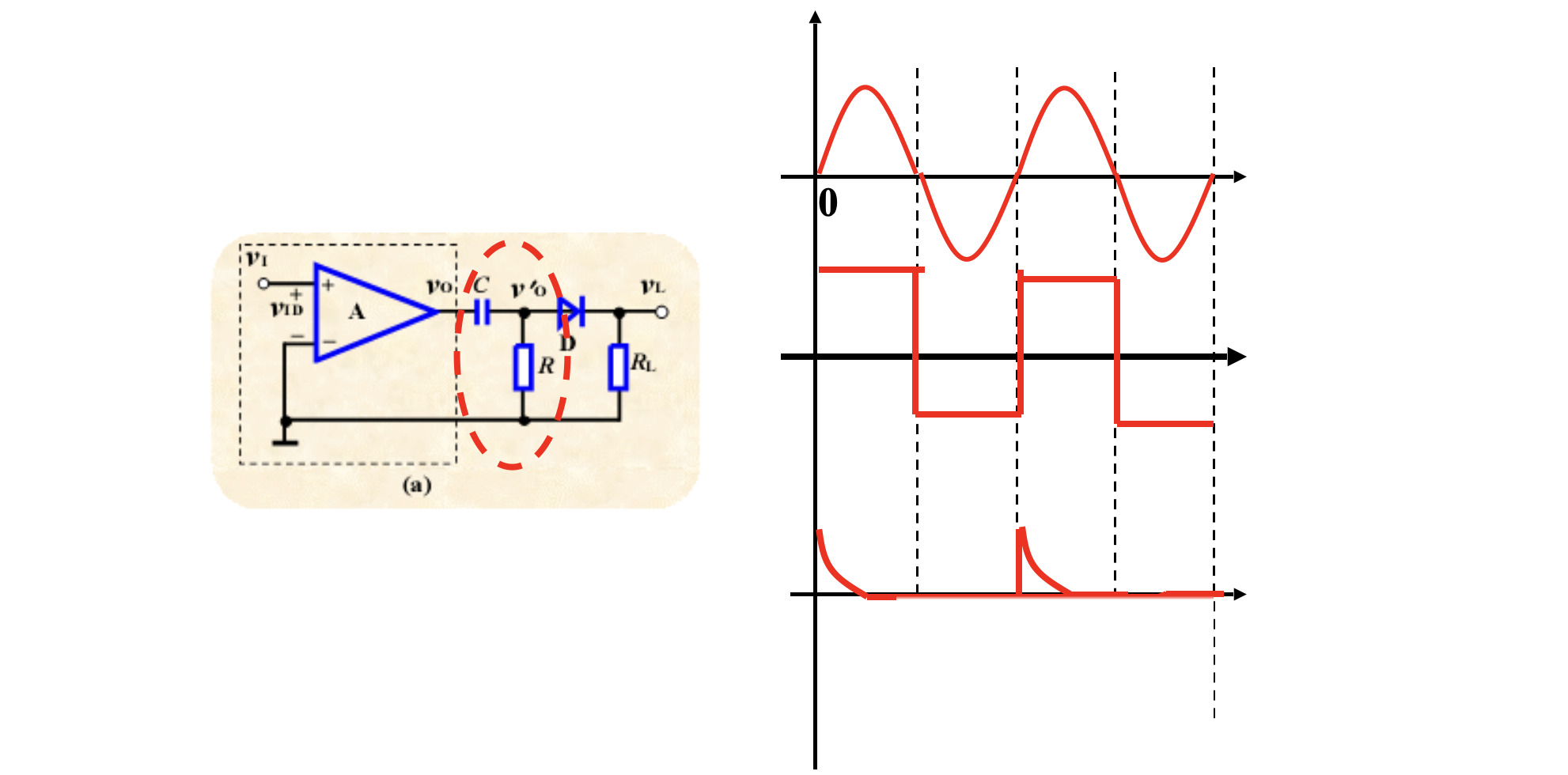
为了尽快到零,要求
窗口比较器
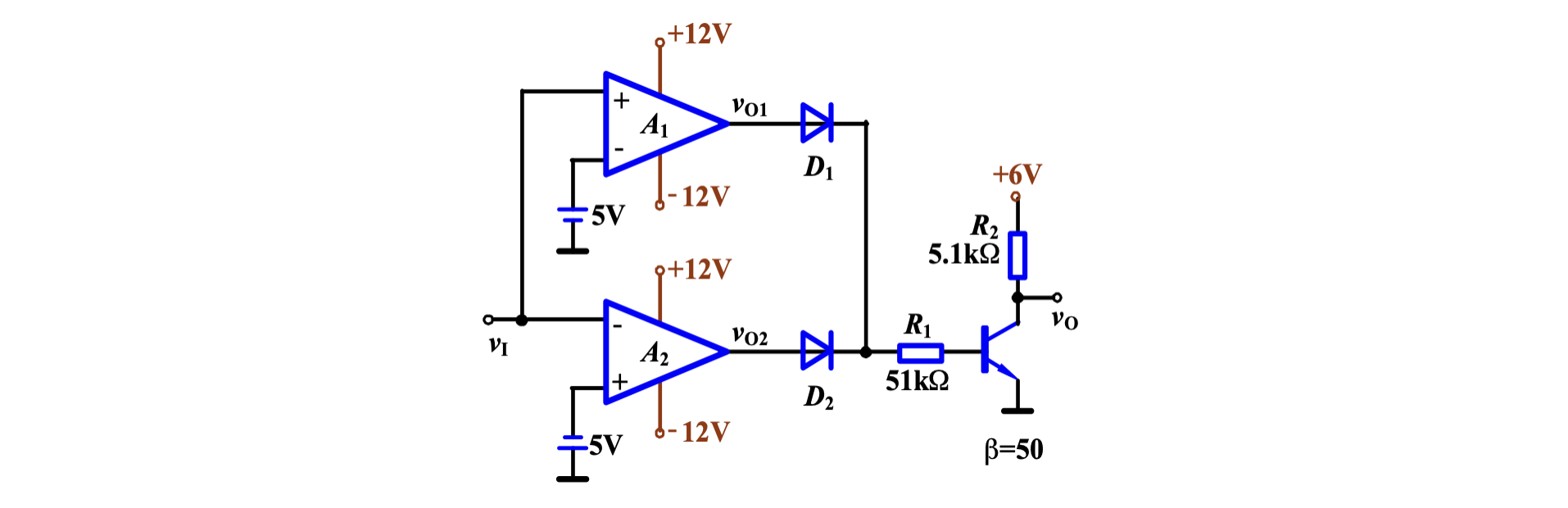
如图电路
- 当
- 当
因此其输出曲线为
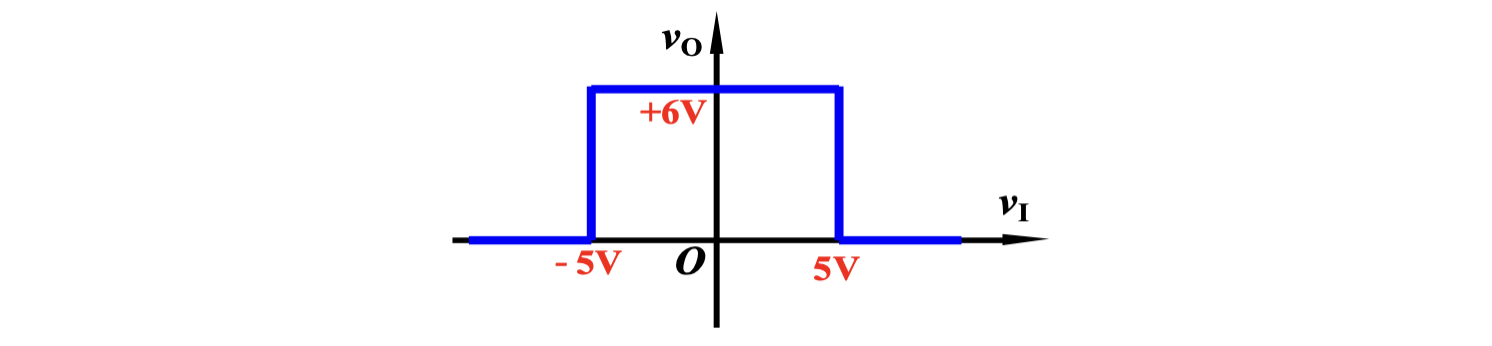
此比较器可以看作是一个有「双边」的比较器,因此又称为窗口比较器(Windows comparator)
2. Schmitt 触发器
若输入电压不稳定,导致在变化过程中与参考电压有多个零点,可能产生多次输出跳变,如图,当输入信号在上升的过程中受噪声影响波动时,
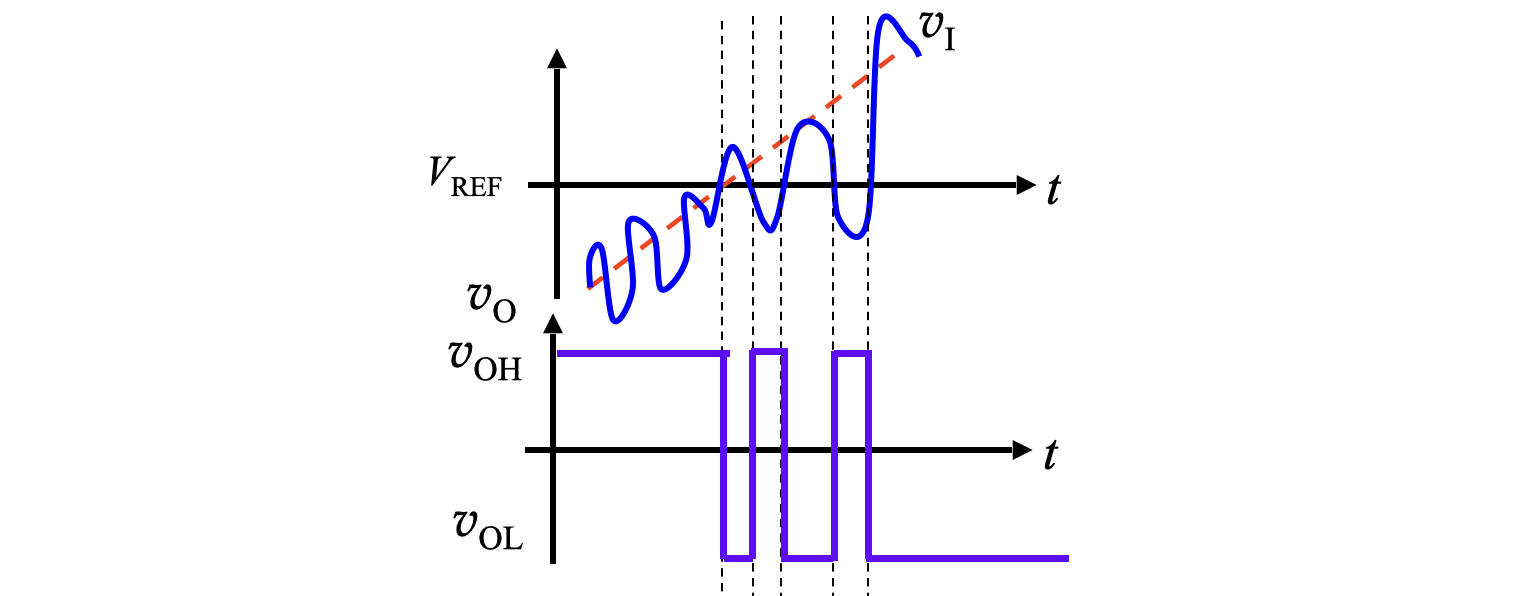
如何为电压在向上和向下变化时设置不同的参考电压?电路中的输出有高低两个值,因此可以把输出引回来,用这个变化量实现变化的参考电压。如下图,将输出电压以正反馈的方式引到同相输入端。
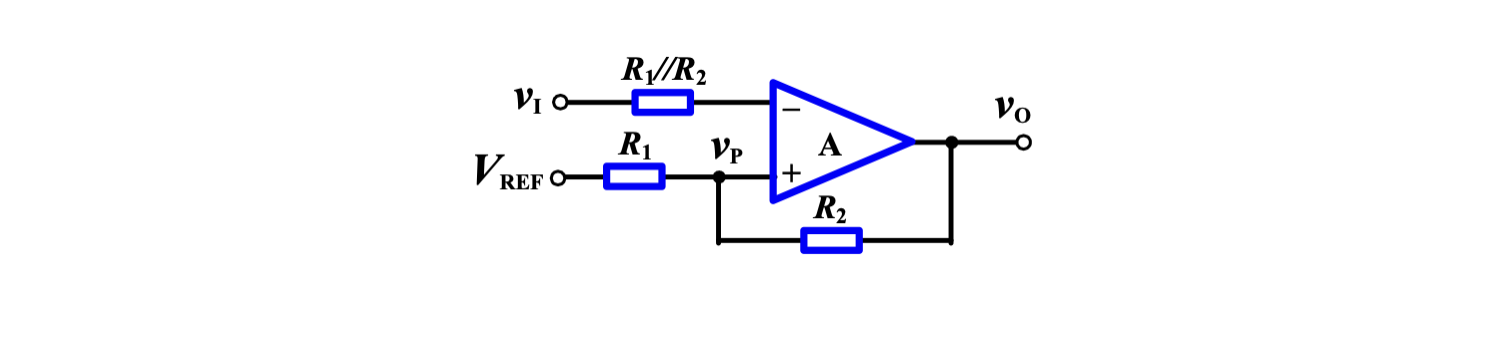
包含正反馈的比较器称为「Schmitt 触发器」。对于图示的 Schmitt 触发器而言,有两个门限电压
把两个门限电压的差叫做「回差电压」(Hysteresis width)
双门限比较器克服了单门限比较器抗干扰能力差的缺点,避免了因噪声产生的反复跳变。
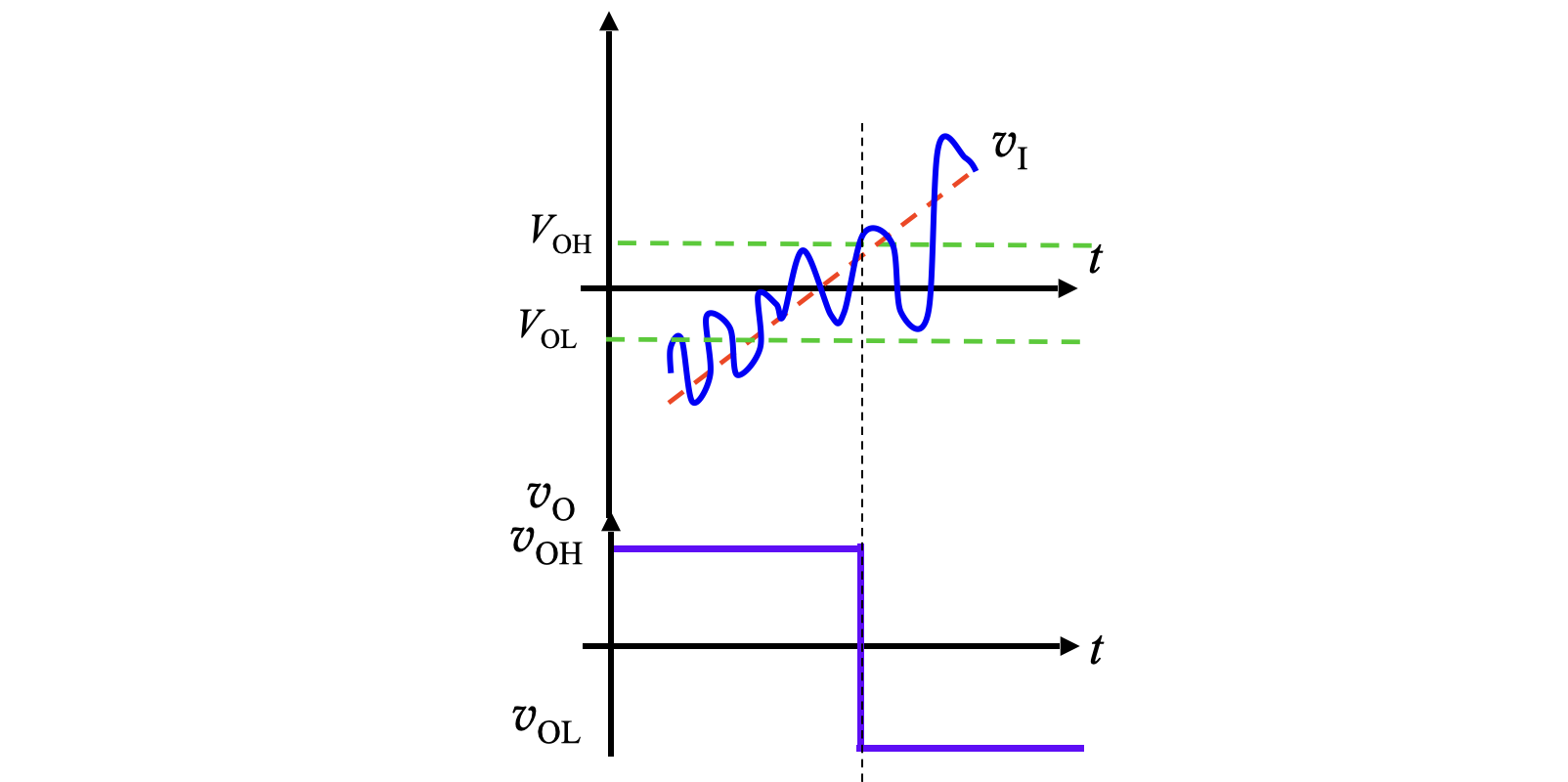
在绘制其传输特性曲线时,先确定输出电压和参考电压,再根据 KCL 方程求出门限电压。
四、非正弦信号的产生
2.1 Schmitt 触发振荡器
将 Schmitt 触发器的参考电压接地,并将输出端通过 RC 串联电路接到输入端,构成「Schmitt 触发振荡器」
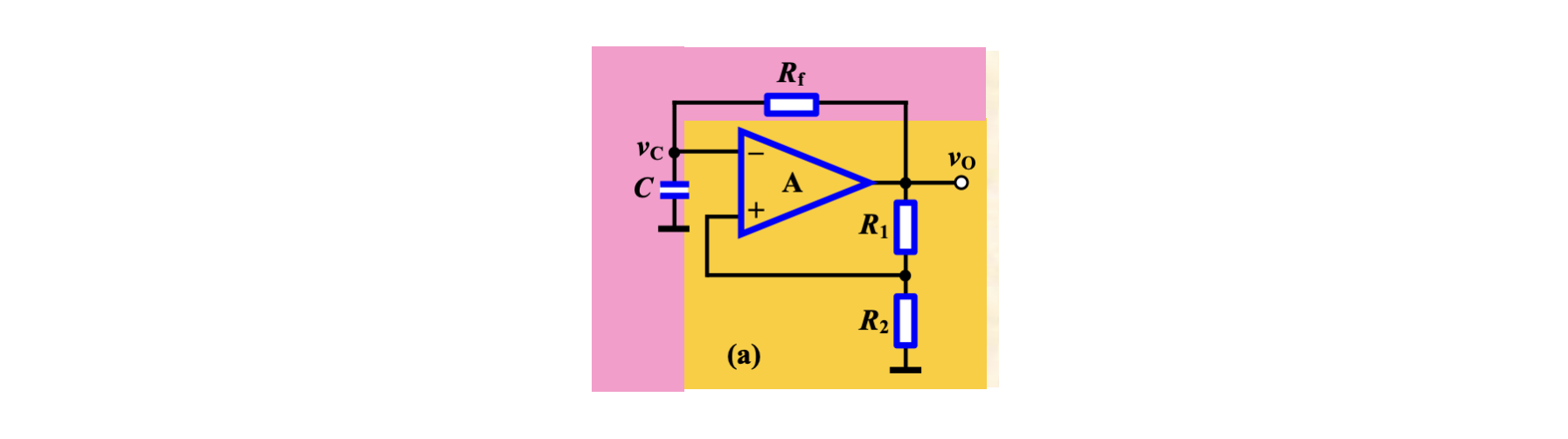
2.2 方波产生器
在 Schmitt 触发振荡器的基础上,在输出端加上稳压二极管从而对输出进行上下限幅,就构成了「方波产生器」。
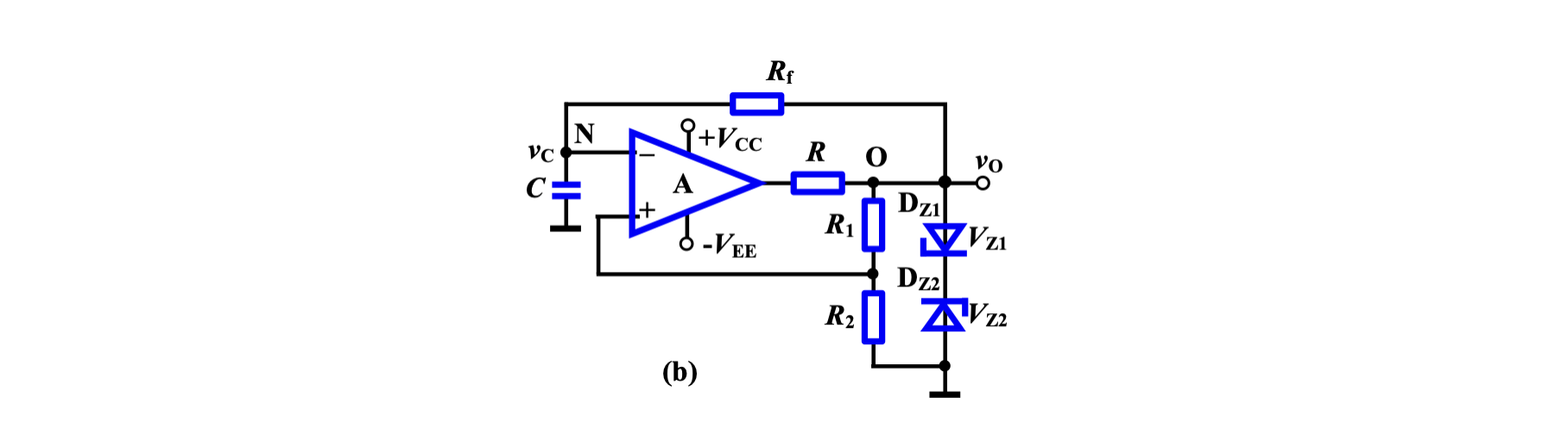
假设上电前是高电平,电容初始电量为零。则上电的瞬间,
在此循环基础上,
2.3 矩形波产生器
在已有方波的基础上,只需要调节占空比,就可以实现矩形波的产生。为了使电容充放电速度不同,将 RC 电路的电阻支路用二极管改为两条不同的电阻支路,从而得到矩形波。

2.4 三角波产生器
在同相输入的 Schmitt 触发器的输出端接上反相积分器,再将输出信号反馈到 Schmiit 的输入端。
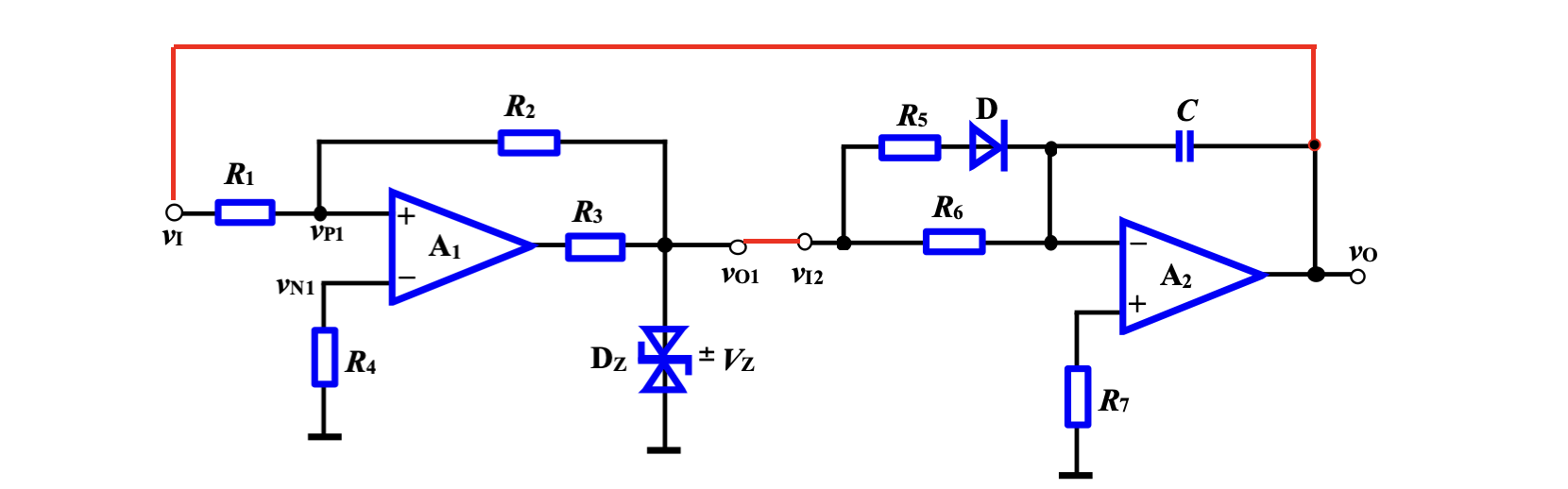
首先分析 Schmitt 触发器,由于存在反馈,因此满足虚短虚短,可以得到
则其两个门限电压分别为
对于反向积分器而言
假设

此电路能够同时输出矩形波和锯齿波。若去掉二极管支路,则积分器对称,输出为三角波。
五、稳压器
本章我们将重点介绍稳压器(Voltage regulator)
1. 交流-直流转换
多数电子产品都需要直流供电,而市电提供的是交流电。为了得到可用的直流电,需要:
- 首先通过降压器得到电压较低的交流电
- 然后通过二极管整流得到正半波。
- 通过 RC 电路进行滤波
- 最后通过稳压器实现稳定的直流输出。
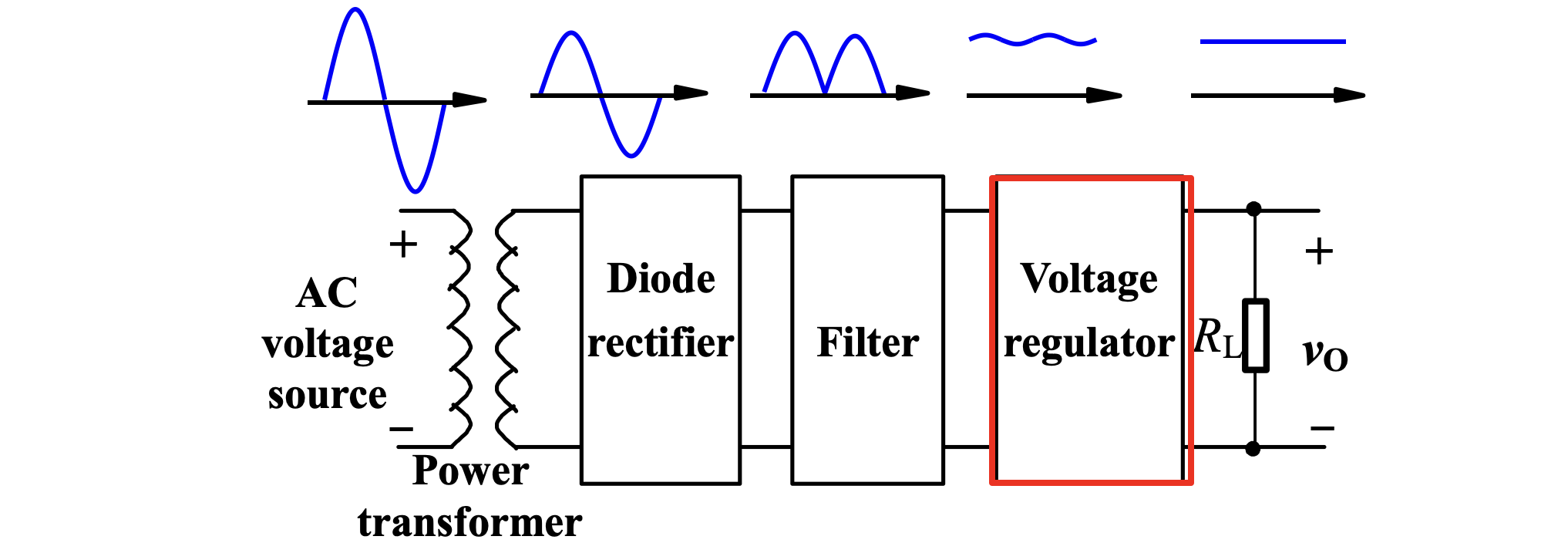
1.1 整流
在二极管一章中已经介绍过桥式整流器的工作原理。
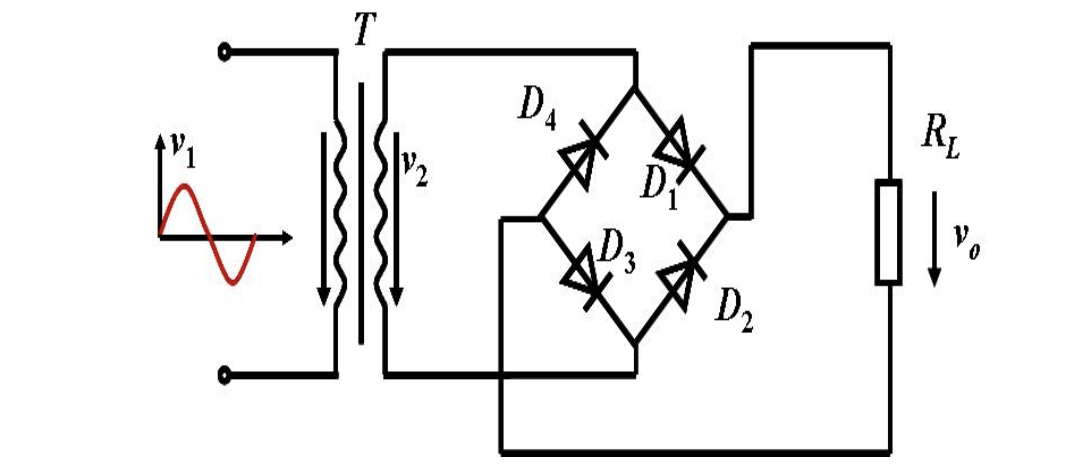
通过桥式整流器后,交流电由正弦波变为单向正弦脉动波。
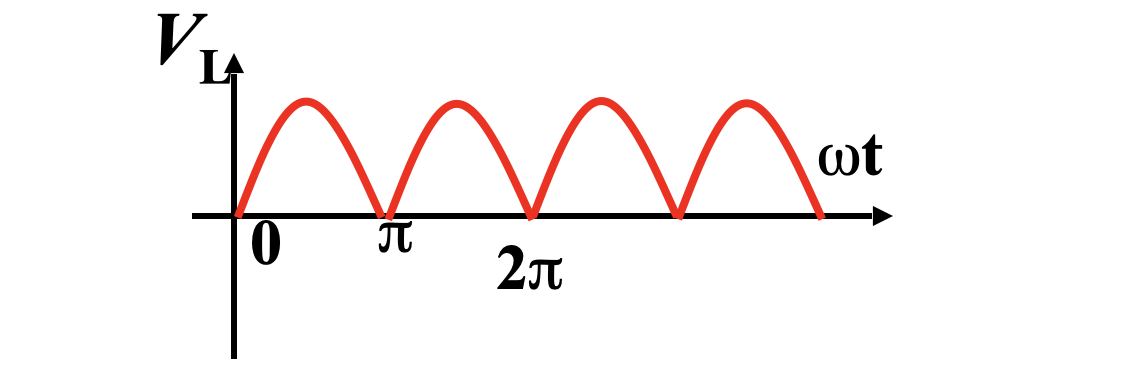
衡量脉动波的一个重要指标就是其平均值,定义为一个周期内电压的积分。
对于正弦波而言,其平均值约为
滤波器
在桥式整流器的后端接上并联的 RC 电路,构成滤波器。滤波器的作用就是使单向正弦波变得更加平整,有利于之后的稳压。
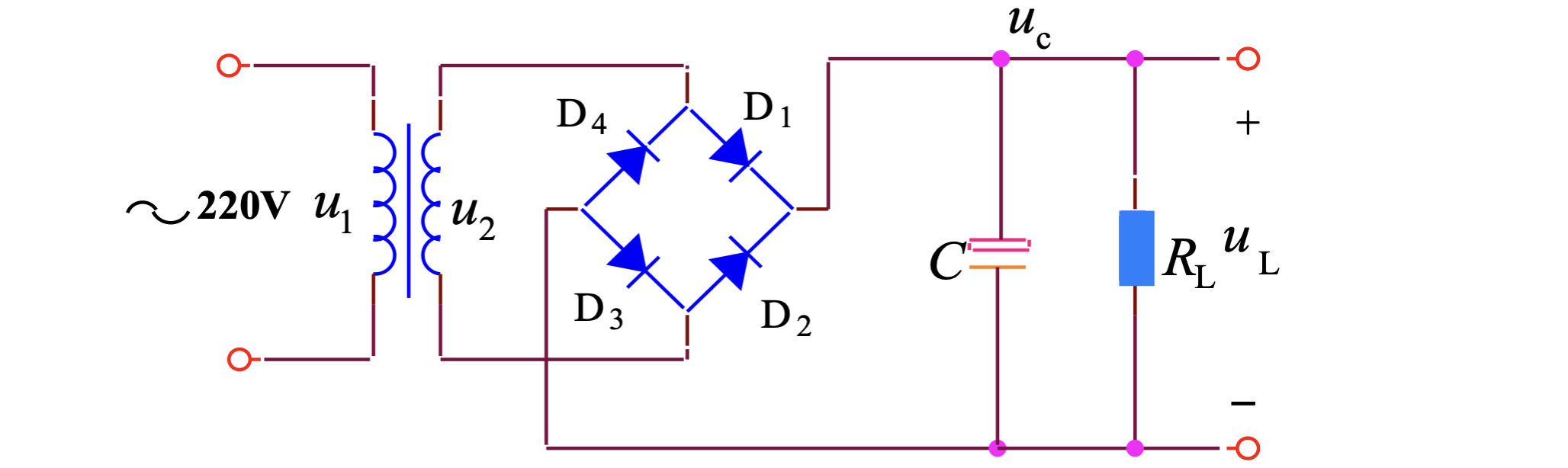
在正弦脉冲的上升阶段,
极端情况下,当
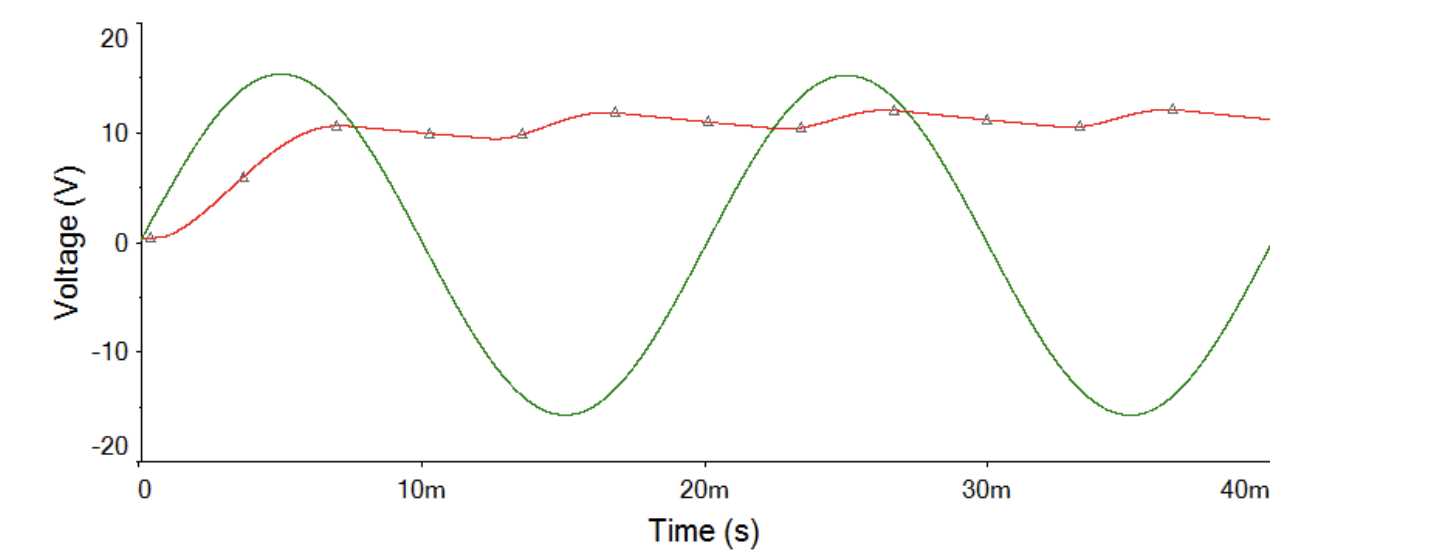
通过滤波器后,已经能实现一个相对稳定的近似直流电压。但实际的输入的交流电电压可能会上下浮动
2. 基础稳压器
2.1 稳压器的引入
要稳定电压,首先想到的就是在输出端连接一个稳压二极管。
但这样简单粗暴的处理方式存在几点不足:
- 稳压二极管的电压特性在出厂时就已经是固定的,因此很难对电路的输出电压进行调整。
- 稳压二极管的电流改变时,电压并非完全稳定
- 在空载时,稳压二极管的电流可能会超过上限。
因此我们可以在稳压管后加上一个运放,对前后级进行隔离。运放输出电流过小,需要在运放的输出端再接一个 BJT,实现足够大的输出电流。由此,我们得到了一个最基础的「稳压器」。
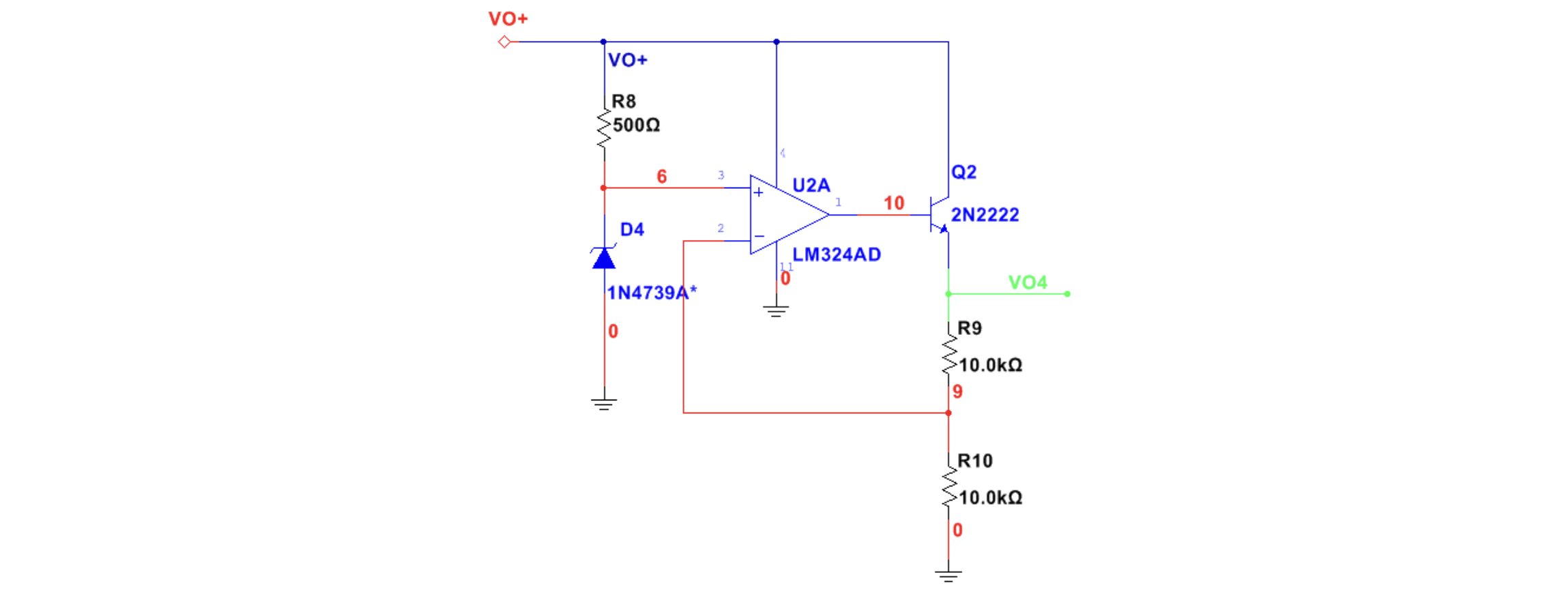
此电路是如何实现稳压的?首先稳压二极管能提供一个相对稳定的电压作为参考电压
比如当挂上小电阻负载导致输出
现在在来回过头看电路各部分的作用,目的是为了让
在运放的反相输入端,我们将输出电压以一个比例
七道大题,最后一题是电源题。改错题可能改反馈类型,要求能够判断出来。电路结构基本不会错,一般出错在极性,如二极管摆放,所有二极管应该都是相同的方向;电容极性;稳压管不能导通,必须反着稳;分压回来的电压信号应作为负反馈。
3. 集成三端运放
3.1 命名方式
以 78L10 为例,其中的“78”表示正电压,“10”表示电压绝对值。
考试要求
两道大题,总分约30
电源一道题,滤波震荡比较一道题