course:
  - 数据挖掘

DIANA 算法

「DIANA 算法」（Divisive Analysis）是一种自顶向下层次聚类，算法开始将所有的对象置于一个簇中，在迭代的每一步，一个簇被分裂为多个更小的簇，直到最终每个对象在一个单独的簇中，或达到一个终止条件。此过程可以看成是AGNES 算法的逆过程

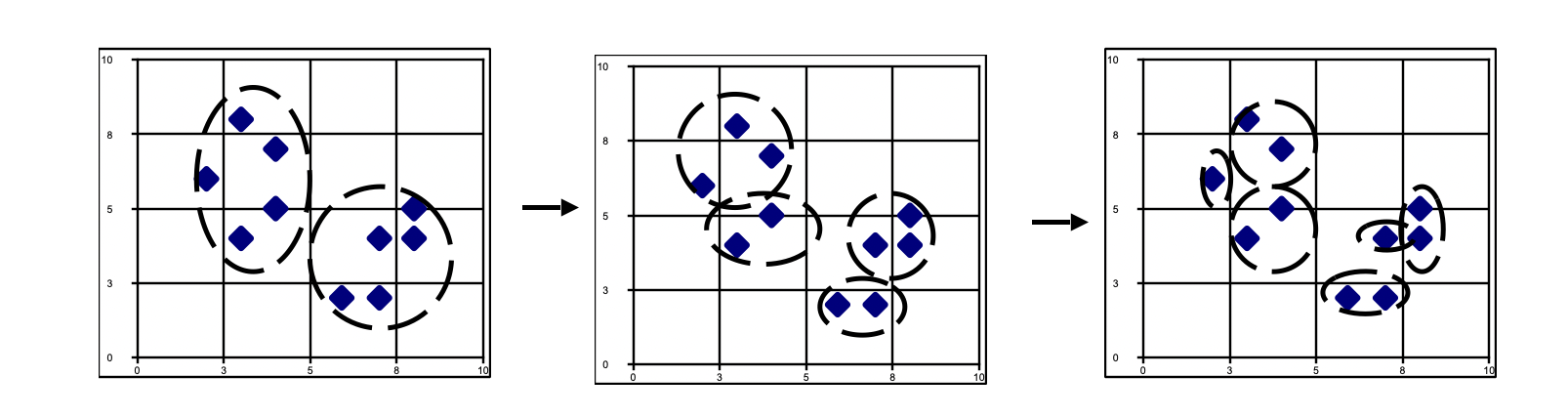
img-2024-04-30 11-11-31.png

在该种层次聚类算法中，也是以希望得到的簇的数目作为聚类的结束条件。同时，使用下面两种测度方法：

簇的直径：在一个簇中，任意两个样本间距离的最大值。
平均相异度（平均距离）

算法

输入：包含个样本的数据集，终止条件簇的数目

输出：个簇，达到终止条件规定的簇的数目

初始时，将所有样本当成一个簇
重复
- 在所有簇中挑选具有最大直径的簇
- 找出中与其他店平均相异度最大的一个点，并把放入 splinter group，剩余的放在 old party 中
- 重复
  - 在 old party 里找出到 splinter group 距离最近的点
  - if (该点到 splinter group 到距离不大于该点与 old party 中其他点之间的最小距离)
    - 将该点加入到 splinter group
- 直到没有新的 old party 点点被分配给 splinter group
- splinter group 和 old party 是被选中的簇分裂成的两个簇，与其他簇组成新的组合
直到达到指定的个簇

例题

给定数据集，使用 DIANA 算法进行聚类

序号	1	2	3	4	5	6	7	8
属性 1	1	1	2	2	3	3	4	4
属性 2	1	2	1	2	4	5	4	5

解：

首先按照 Euclidean 距离计算出相异性矩阵

开始时，所有样本在同一个簇中。根据 DIANA 算法，计算各个样本之间的平均距离。首先计算 1 号样本到其他样本的平均距离

同理得到

注意到 1 号样本和 8 号样本平均距离最大。这里选 1 号样本进入 splinter group。剩下的其他样本为 old party，解下来找出距离 splinter group 距离最近的样本，并且该样本到 splinter group 的距离不大于该样本与 old party 中其他样本之间的最小距离，则将该样本放入 splinter group 中。根据相异性矩阵，第二个样本到第一个样本的距离不大于其他 old party 的最小距离（都等于 1），因此加入了 splinter group

再看第三个样本，同样满足到第一个样本的距离不大于其他 old party 的最小距离（都等于 1），因此也加入了 splinter group

重复，第四个样本也加入了 splinter group。在这之后已找不到可以放入 splinter group 中的样本，并且此时达到算法的终止条件（），算法结束。得到的两个簇为